自由活塞斯特林制冷机动力吸振器设计及实验研究

2021-02-02倪贤灿

真空与低温 2021年1期

倪贤灿，陈曦，凌飞，郑朴，洪昊

（上海理工大学能源与动力工程学院，上海 200093）

0 引言

近年来，随着红外探测、高温超导、低温医疗等技术的迅速发展，对高效率、轻量化制冷机的需求越来越急迫。斯特林制冷机作为回热式低温制冷机[1]，因其采用环保工质氦气、结构简单紧凑、效率高等得到了广泛应用与发展。然而FPSC在运行过程中会产生一定的振动力，影响制冷机工作与应用性能。大量实验研究发现，斯特林制冷机振动谐波主要是由基频和一系列高阶倍频组成，其中基频占主要成分。基频一般是压缩机的驱动频率，高阶倍频谐波来自于气体、弹簧和机械结构的非线性因素[2]。斯特林制冷机的振动控制分为主动控制和被动控制两类。其中，主动振动控制系统主要由振动测量传感器、控制器与吸振器组成，通过主动调节输出控制信号来驱动吸振器，在各个离散谐波频率处均产生与制冷机振动力大小相等方向相反的简谐力，从而实现振动抵消[3−5]。被动控制分为被动式隔振、被动式阻尼减振以及动力减振三类[6]，被动式隔振是在制冷机冷头端与被冷却器之间安装隔振器，减小振动对被冷却器的影响；被动式阻尼减振利用阻尼消耗振动能量，使瞬态振动迅速衰减；动力减振通过添加弹簧质量系统使振动减小。鉴于动力减振具有结构简单、不额外耗能、可靠性高等优点[7]，本文采用被动控制减振方案作为自由活塞斯特林制冷机减振器，并对动力吸振器进行理论研究、结构设计及实验验证。

1 动力吸振器理论分析

1.1 吸振器的动力学理论分析

自由活塞斯特林制冷机运行时频率f保持恒定，可利用动力吸振器来抵消整机振动。图1为二自由度系统受迫振动模型。

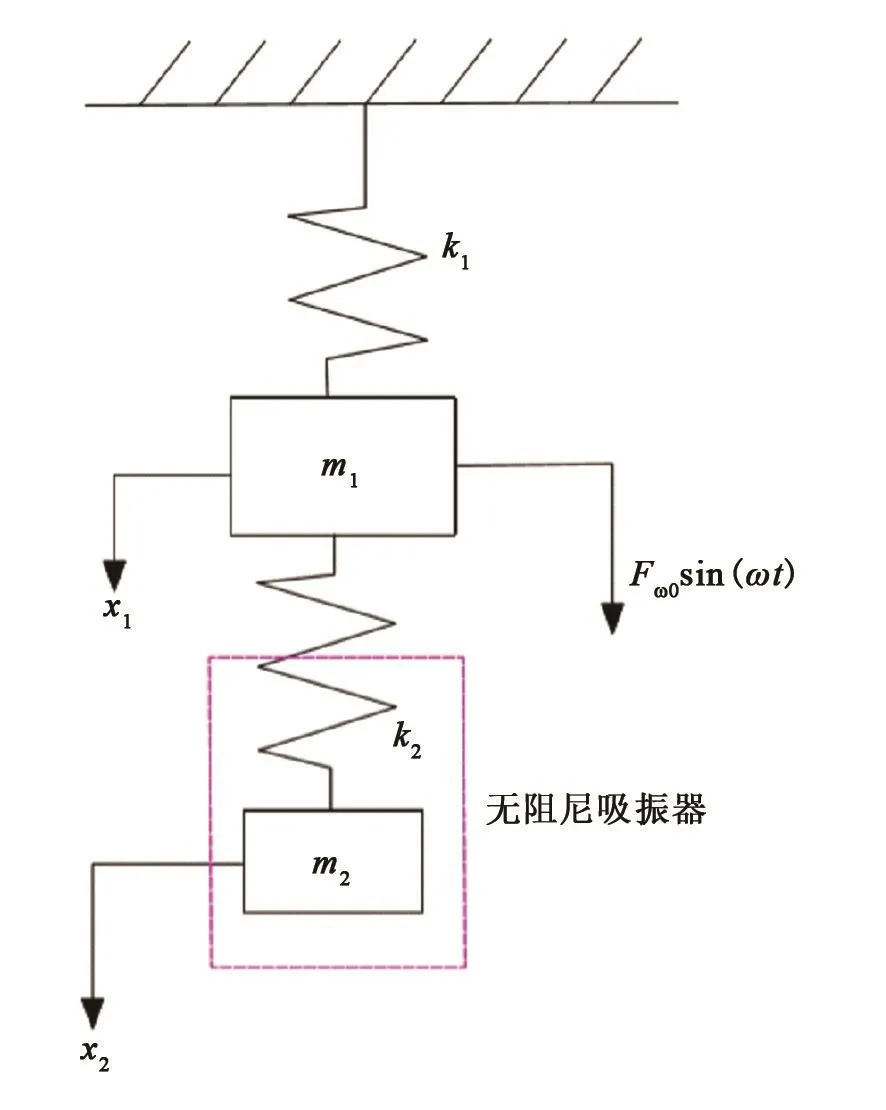
图1 二自由度系统受迫动力学模型Fig.1 Forced dynamics model of a two-degree-of-freedom system

质量为m1的整机系统受到振幅为Fω0，角频率为ω的简谐振动，与弹簧刚度为k2和质量为m2的无阻尼动力吸振器连接，忽略整机活塞运行过程产生的摩擦阻尼，其运动方程为：

式（1）经拉普拉斯变换，求解得：

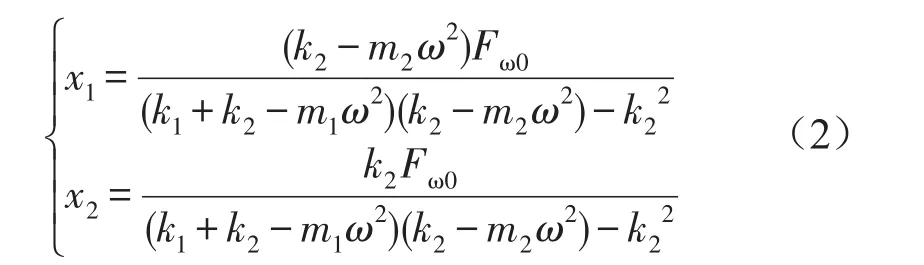
由式（2）可知，当k2=m2ω2时，即制冷机运行频率等于吸振器固有频率，整机位移x1为0，吸振器可有效减振。从上述公式可以看出，当运行频率与弹簧刚度一定时，可通过改变吸振器动子质量来实现频率的匹配。

1.2 吸振器弹簧结构理论分析

涡旋臂型柔性弹簧广泛应用于小型低温制冷机，图2为等槽宽涡旋臂型柔性板弹簧结构示意图，弹簧片外侧有四个圆周固定孔，用于连接质量块，中心固定孔用于连接减振杆。其中，Ds为涡旋臂型柔性弹簧的外径，Ls为涡旋臂长，ws为涡旋臂宽。由于直线臂型柔性弹簧的直臂相对于涡旋臂更适合进行简单的分析计算，Marquardt等[8]通过对两端夹紧的悬臂梁进行分析，得出了直线臂型柔性弹簧性能的计算公式。用该公式也可定性分析涡旋臂型柔性弹簧的结构参数对弹簧性能的影响，并作为减振弹簧型线设计的依据[9]。

图2 等槽宽涡旋臂型柔性弹簧的结构示意图Fig.2 Schematic diagram of the structure of the equal groove width scroll arm type flexible spring

较小的疲劳应力是保证柔性弹簧长寿命可靠运行的关键，通常须要把弹簧的最大应力控制在材料疲劳极限的80%,最大应力σmax表达式：

式中：n为弹簧臂数，图2中n=4；E为弹性模量；ts为弹簧厚度；s为活塞行程；Ls为涡旋臂长度。

由式（3）可知，最大应力σmax随着弹性模量E、弹簧厚度ts、活塞行程s的增加而增大，随着涡旋臂长度Ls的增大而减小。

轴向刚度kz和径向刚度kr的表达式为：

式中：Ns为弹簧片数；ws为涡旋臂宽。

由式（4）、式（5）可知，轴向刚度kz与弹簧厚度ts的三次方成正比，径向刚度kr与涡旋臂宽ws的三次方成正比。G是一个关于s∕Ls的函数，用于阐明径向刚度kr随着弹簧轴向位移的增加而减小。弹簧在最大轴向形变时对应的径向刚度会比无轴向形变时小一个数量级[8]，当轴向位移为0时，G（0）=1。图3所示为变槽宽涡旋型柔性弹簧，涡旋臂宽ws不是一个常数，它随着涡旋臂长的变化而变化。由式（4）和式（5）可知，在设计板弹簧时，若刚度达不到给定要求，可以增加ws以增加刚度，实现变槽宽涡旋臂型弹簧的设计。

图3 变槽宽涡旋臂型柔性弹簧结构示意图Fig.3 Schematic diagram of variable slot width scroll arm type flexible spring

2 吸振器设计及模态分析

图4为自由活塞斯特林制冷机实物图，吸振器一般安装于制冷机底部以抵消整机振动。吸振器主要由减振杆、固定螺钉、减振弹簧、减振质量块和垫片组成，如图5所示。吸振器的优化设计主要涉及板弹簧型线选择、结构布置形式选择以及质量与刚度的匹配等。

图4 自由活塞斯特林制冷机实物图Fig.4 Free Piston Stirling Cooler

图5 吸振器实物图Fig.5 The shock absorber

2.1 弹簧型线选择

图2和图3分别为等槽宽型与变槽宽型减振板弹簧，利用Ansys Workbench中的Static Structural模块对两种型线的弹簧进行有限元分析。其中，板弹簧材料为不锈钢，型线长度均为184 mm，外径和厚度均相等，轴向荷载力为1 N。图6所示为减振弹簧位移分布，等槽宽型减振弹簧最大位移为0.076 6 mm,变槽宽型减振弹簧最大位移为0.029 0 mm,可知变槽宽型减振弹簧的轴向刚度要远远大于等槽宽型减振弹簧的轴向刚度，有利于延长弹簧的运行寿命。图7为两种不同型线减振弹簧处于3.5 mm单侧轴向位移时对应的应力分布云图，其中等槽宽型减振弹簧最大应力为321.04 MPa，而变槽宽型减振弹簧最大应力为351.57 MPa，两者均满足应力要求。综合考虑，本设计选用变槽宽型减振弹簧。

图6 1 N外力下减振弹簧位移分布云图Fig.6 Displacement cloud diagram of damping spring under 1 N external force

图7 两种不同型线减振弹簧处于3.5 mm单侧轴向位移时对应的应力分布云图Fig.7 Stress distribution of two kinds of shock absorber with different profiles at 3.5 mm unilateral axial displacement

2.2 结构形式选择

吸振器结构形式有中心孔连接外壳体和圆周孔连接外壳体两种，前者通过外圆部分吸收振动，后者则在中心部分吸收振动。图8为设计的变槽宽型减振弹簧在不同结构形式下处于3.5 mm单侧轴向位移时对应的应力分布云图。采用中心孔连接外壳体时，最大应力为351.57 MPa，位于型线尾端；而圆周孔连接方式的最大应力为358.42 MPa，位于型线始端。中心孔连接方式的应力低于圆周孔连接，且中心孔连接方式的结构更简单，装配更方便，故吸振器采用该结构形式。

2.3 质量与刚度匹配

由式（2）可知，当吸振器固有频率接近运行频率时，根据二自由度系统的反共振特性，即可有效地吸收整机振动力，故须对吸振器进行质量与刚度匹配，使其接近制冷机运行频率。本文设计了三种型号的吸振器，分别为：a——小质量块−单片板弹簧型；b——中等质量块−两片板弹簧型；c——大质量块−三片板弹簧型。在三维设计软件中，调整减振块结构尺寸并赋予相应材料属性，优化运动组件质量，使固有频率达到设计范围，设计结果如表1所列。其中，吸振器a、b、c的设计固有频率值分别为81.45 Hz、79.98 Hz、80.14 Hz，制冷机设计总质量为3 169 g，可得三种吸振器的总运动质量与整机设计总质量的比值分别为0.04、0.09、0.13。

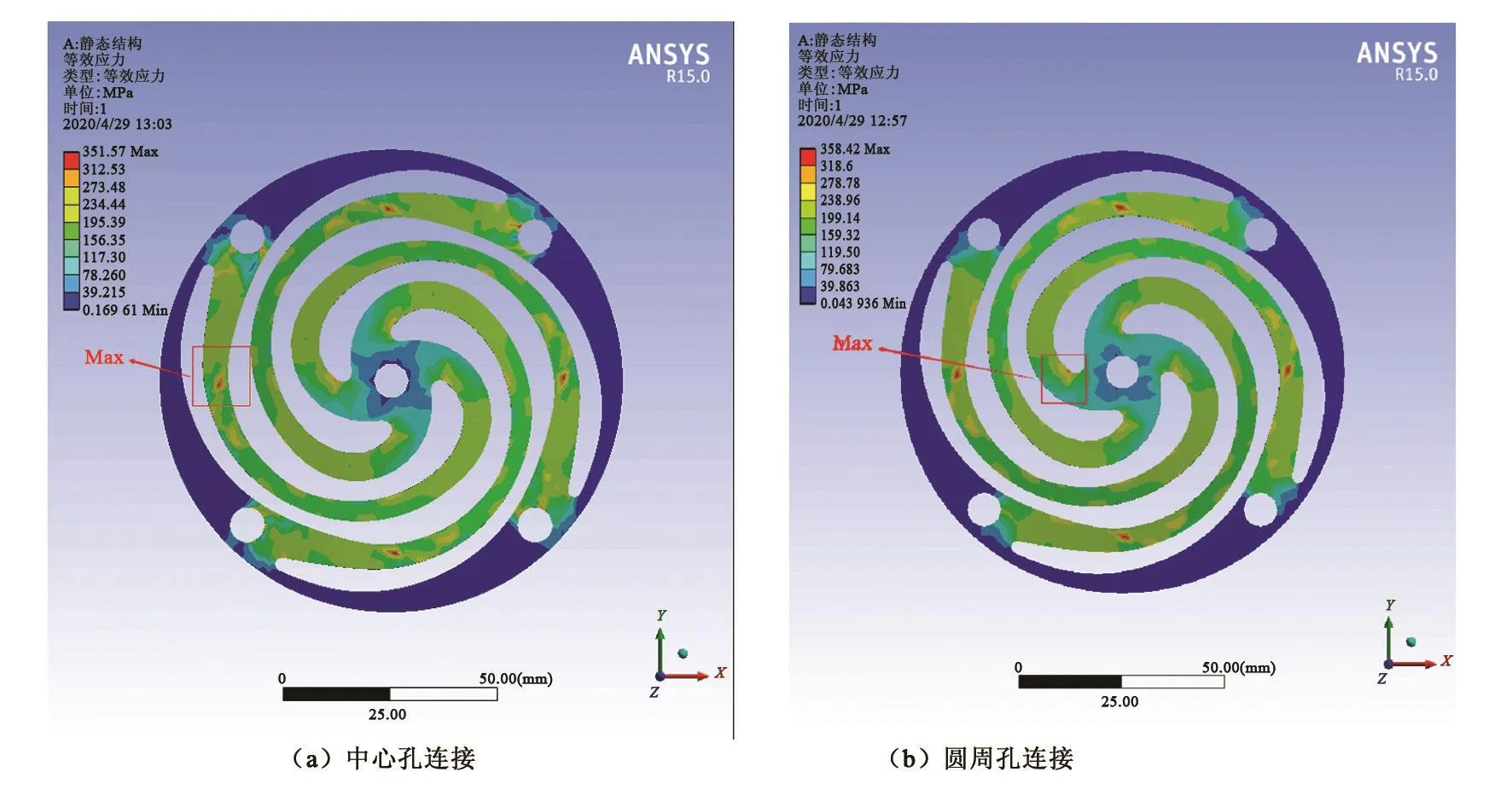
图8 变槽宽型减振弹簧在不同结构形式下处于3.5 mm单侧轴向位移时对应的应力分布云图Fig.8 Stress distribution of variable groove width type shock absorption spring under different structual arrangements at 3.5 mm unilateral axial displacement

表1 三种吸振器模拟优化结果Tab.1 Simulation and optimization results of three kinds of shock absorbers

2.4 一阶模态分析

利用Ansys Workbench中Modal模块对三种吸振器进行有限元分析，模拟各吸振器在一阶模态时的固有频率及模态振型。定义各零件之间的接触类型（contact region）为bonded，材料设置为structural steel。

图9为吸振器b在3 ms内的运动位移云图，当t=0 ms时，吸振器处于静止状态，t=0.6 ms时，吸振器b的外圆周开始运动，t=1.2～2.4 ms，吸振器b的外圆周振动开始加剧，直到t=3 ms时，振动达到最剧烈，而中心孔部分始终无明显位移。由此可见，采用中心孔连接结构的吸振器振动集中在外圆周部分。

图10所示为a、b、c三种吸振器的一阶模态结果，最大形变量分别为84.908 mm、59.493 mm、48.803 mm，随着总动子质量和总弹簧刚度的增大，吸振器外圆周总形变量幅值减小。根据一阶模态分析结果得知，a、b、c吸振器的固有频率模拟分别为75.734 Hz、79.561 Hz、80.572 Hz，与计算值误差最小的是中等质量块−两片减振弹簧型吸振器，其误差仅为0.5%。

此外，考虑到制冷机与吸振器加工误差的存在，实际情况下并不能完全消除整机振动力，仍将存在部分振动影响，为避免因吸振器振幅过大降低板弹簧寿命，一般情况下吸振器运动质量设计值与整机质量设计值之比应大于或者接近于0.1，结合模态分析结果与轻量化需求，拟优选吸振器b。

图9 吸振器b在3 ms内的运动位移云图Fig.9 Displacement cloud diagram of vibration absorber b within 3 ms

图10 吸振器a、b、c的一阶模态图Fig.10 First-order modes of vibration absorbers a，b，c

3 吸振器工作性能扫频实验

对设计加工的吸振器a、b、c分别进行减振性能测试与验证，确定三种吸振器的实际最优工作频率与减振效果，图11为三种吸振器的实物图。吸振器性能测试一般采用直接观测、高速摄影机测试、加速度传感器测试、应变片式位移传感器测试等方法。由于应变片式位移传感器结构简单，安装方便，测量范围较广，本文采用应变片式位移传感器测试方法。其中，应变片由敏感栅、引线、黏结剂、基片和覆盖层等部分组成，敏感栅是电阻应变片里的金属丝，电阻随着金属丝长度变化而变化，可将位移信号转化为电信号[11]，其信号峰值为最大位移形变量的微应变（με）。

根据一阶模态分析结果，将应变片式位移传感器安装于总变形量最大的减振弹簧外圆周部分，将制冷机控制在输入功为85 W、输入电压为14 V的工况下，分别对三种吸振器做扫频实验，确定其最优工作频率即共振点，验证其减振效果。

图11 三种吸振器实物图Fig.11 Three kinds of physical drawings of shock absorbers

通过读取信号峰值确定并分析各吸振器的最大变形量，图12为三种吸振器扫频实验结果。外部激振力从66 Hz增加到71 Hz时，吸振器a的外圆周总形变量先缓慢增大后急剧增大，在固有频率附近达到最大值；当激励频率从71 Hz增大到76 Hz时，总形变量急剧下降，有效减振频率区间为70～72 Hz。同理可知，吸振器b、c的有效减振区间分别为76～78 Hz、77～79 Hz。吸振器a在其共振点处的信号峰值最大，b次之，c最小，与模态分析结果相符。吸振器a、b、c的共振频率分别为71 Hz、77 Hz、78 Hz，频率误差分别为13%、3%、3%，而吸振器a误差较大是因为其实际运动质量远大于设计运动质量，导致共振点左移。

吸振器a、b、c的各项设计值、模拟值、实测计算值及实验值参数对比如表2所列。其中，三种吸振器的共振频率实验值均小于设计值、模拟值以及实际测量后的计算值，主要是因为减振弹簧的实际轴向刚度略小于设计值34 455 N∕m，经实验值反推计算，弹簧刚度应在31 000 N∕m左右。基于频率误差、质量比以及减振弹簧振幅等参数分析，优选吸振器b。b型吸振器的实验值为77 Hz，可调整质量块的质量来使得其固有频率满足设计目标。