以最佳温度均匀度为目标的常压热循环系统结构参数优化

2021-02-02张婉雨吴静怡李春煜王珊珊

真空与低温 2021年1期

张婉雨，吴静怡*，李春煜，王珊珊

（1.上海交通大学制冷与低温工程研究所，上海 200240；2.上海卫星装备研究所，上海 200240）

0 引言

近年来，随着航天航空技术的不断发展，航天探测逐渐向深空迈进，这需要航天器能够在越来越恶劣的空间环境中长期生存[1−2]。为了确保航天器可以在温度较低的环境中正常运行，须在研制阶段进行大量地面热试验，提前发现工艺缺陷[3]。热循环试验因具有结构简单、运行成本低、试验周期短的优点，已越来越多地被应用于航天器地面环境试验中[4]。在低温情况下对试件模型进行缺陷诊断时，重要的一环是对其进行降温以达到试验所需温度。在整个降温过程中，不仅要求试件模型在规定时间内达到目标温度，并且要将降温过程中的温度均匀度控制在一定范围内，避免试件模型由于温度不均而产生热变形，造成损伤。

为了完成对试件模型的降温，试验系统要借助低温流体与模型间的对流换热，达到降低温度的目的。由于试验箱体尺寸大，且低温流体与模型间温差较大，故试验箱体内传热模式为以混合对流为主的导热、对流及辐射的耦合传热。针对竖直方管内的混合对流，许多学者进行了相关研究。Barletta[5−6]对充分发展段的竖直矩形通道混合对流问题进行了理论求解，并获得Nu数、Gr数和Re数间的关系。Yang等[7−8]对于竖直方管的流动及混合对流传热特性进行了研究；黄一也等[9]针对湍流状态下的混合对流进行了仿真模拟，提出了壁面Nu随Re与Gr的变化规律，并得出相应关联式。对于导热、对流、辐射耦合传热等方面的问题，近几十年来很多学者对不同研究对象中的耦合传热进行了理论及实验研究，如Balaji等[10]对二维槽道内的耦合传热问题进行了仿真模拟，并得到了相应条件下壁面Nu关联式；Martyushev等[11]分析了含有内热源的二维腔体内的耦合问题，得出了Nu与Ra、流固导热系数比以及壁面厚度间的影响规律及相应关联式。由于条件限制，上述关于耦合传热的研究大多集中于二维对象，且多为稳态传热下的规律。在常压热循环试验系统中，由于航天器的不对称性，耦合传热与流动难以进行二维简化，多为三维非稳态。目前的研究机制无法对三维模型进行描述，不适用于大尺寸模型的降温过程。

本文通过数值模拟方法，对放置试件模型的航天器热循环试验箱内流−固−热耦合降温过程进行研究，分析在不同的模型摆放方式及流道布置下，试验箱内流体的流动与传热特性，得到不同结构参数，试验箱内模型的平均温度和温度分布均匀性的变化规律，为以后热循环试验系统结构参数选取及优化提供指导意见。

1 物理模型与数学模型

所采用试件的物理模型如图1所示。主要对降温过程进行仿真分析，在降温过程中，低温流体以恒定的温度、恒定的流量流入长宽高为10 mm×6 mm×8 mm的试验箱体内。低温流体与试验箱内试件模型进行换热后，带走试件模型自身热量，达到降温的目的；当试件模型平均温度达到255 K，即高于入口平均温度2 K时，认为降温过程完成。在整个换热过程中，假设壁面处于绝热状态，且模型在试验箱体内的位置固定，采用无滑移假设。试验箱体内流体为干燥空气，流速较低，视为不可压流体。流体密度采用Boussinesq近似，仅考虑密度变化对体积力的影响。流体的其他物性在仿真计算中视为常数。仿真中使用的流体及固体物性参数如表1所列。

图1 仿真计算中试验箱体物理模型示意图Fig.1 Schematic diagram of test chamber used in simulation calculation

表1 流体及固体物性参数Tab.1 Fluid and solid parameters

试件模型为薄壁结构的圆柱体，壁厚为10 mm，材质为Al。利用ANSYS平台下FLUENT 16.0进行仿真计算，湍流模型选择transition SST−k−ω模型。采用非均匀网格进行计算，为了更精确地对流场、温度场进行模拟，对试件模型附近边界层流动进行了局部网格加密，以满足边界层网格要求。

除此之外，为了研究试件形状对换热的影响，引入表征形状的高径比：

式中：hcy与dcy分别为圆柱试件模型的高与底面直径。

为了对不同结构参数下的热循环系统的降温效果进行对比，对温度进行无量纲化处理。无量纲温度表示为：

式中：T为箱体空间温度；Te为环境温度及初始时箱体空间温度；Tin为入口流体温度。

引入平均无量纲温度量化降温速率，引入无量纲温度极差与无量纲温度标准差量化温度均匀度。其中平均无量纲温度表示为：

式中：V为箱体体积。

无量纲温度极差表示为：

无量纲温度标准差表示为：

2 仿真结果分析

采用上述模型对热循环系统降温过程进行仿真计算。为保证仿真结果的准确性，首先对网格进行了无关性验证。国军标规定了试验箱为空箱时的温度均匀性，在空箱实验中，制冷过程采用上进下出的方式容易达到规定的指标。因此在进行结构参数优化研究之前，对放有试件模型的试验箱体在上进下出方式下的降温过程进行研究。此过程的具体试验工况为：流体在入口处的流速为0.1 m∕s（体积流量为2.16×104m3∕h），入口处流体温度为253 K，试件模型位于整个试验箱体的中间，底面距离箱底3 m。计算所得相关参数如图2所示。可以看出，随着网格数量的增加，试验箱体内全局无量纲平均温度及试件模型无量纲温度均匀度均单调递减，并逐渐趋于某一数值。为了在保证足够精确度的情况下提高运算速度，采用338万个网格数进行一系列的仿真模拟。此外，依据国军标GJB 150A对于温度测点的布置要求并考虑试验空间的对称性，利用黄一也等[9]试验结果，在相同工况下（图3）对仿真所用数学模型进行计算。仿真与试验所得结果如图4所示。从图中可以看出，壁面附近偏差小于1%，仿真与试验最大偏差小于2.5%，这说明仿真计算所选用模型能够准确反映试验箱体在实际运行中的温度分布。

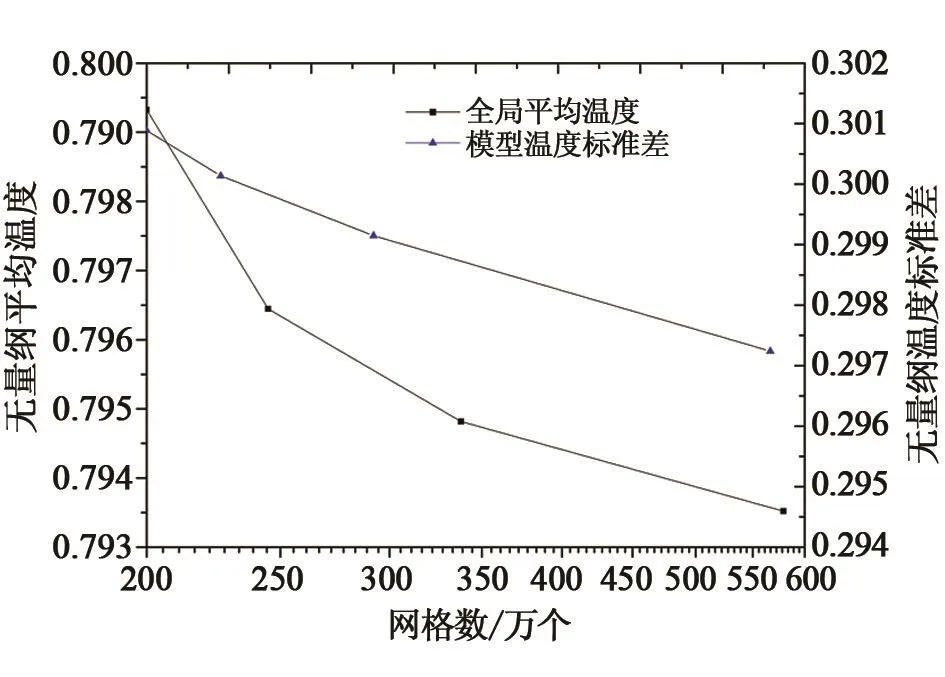
图2 网格无关性验证曲线Fig.2 Results of the grid independence verification.

图3 试验系统温度传感器布置示意图Fig.3 Schematic diagram of temperature sensor arrangement in the test system

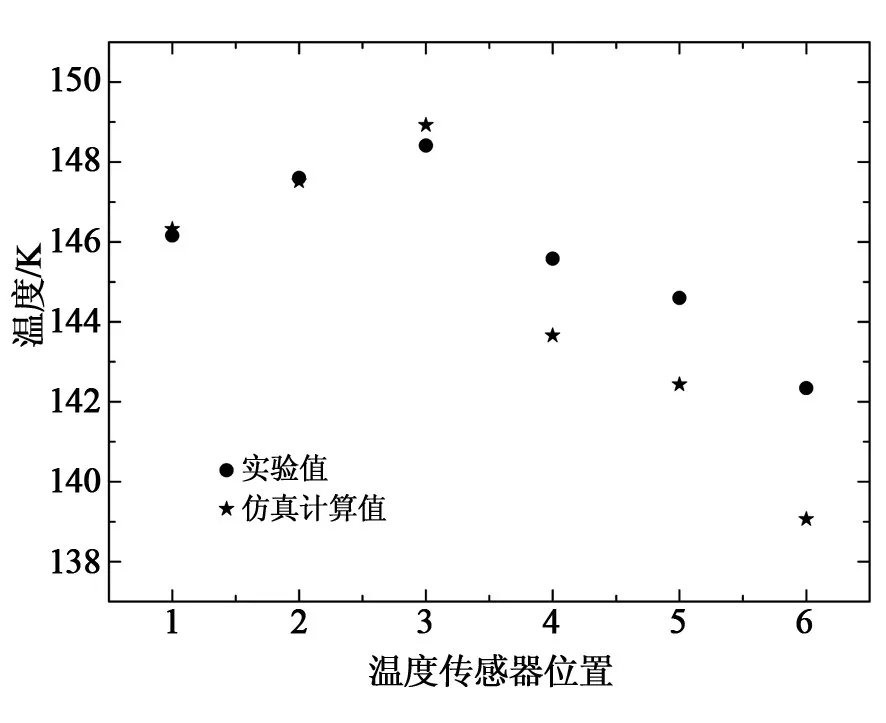
图4 稳态温度模拟与试验结果对比曲线Fig.4 Comparison of steady state temperature by simulation and experiment

图5（a）、（b）分别为有试件模型时，降温2 h之后过中轴线Y−Z截面上试验箱体内的温度分布以及竖直方向的速度分布。从图5（a）中可以看出，在降温2 h之后，箱体外流域温度基本已经与入口温度相同，但在试件模型下部与出口间出现一个锥形高温区域，温度与环境温度相同。从试件模型及模型内流域温度可以看出，试件模型侧面降温速率最大，上部降温速率快于底部。结合竖直方向上流体流动速度分布可以看出，试件模型侧面流体流速较大，通过混合对流与试件模型进行换热。

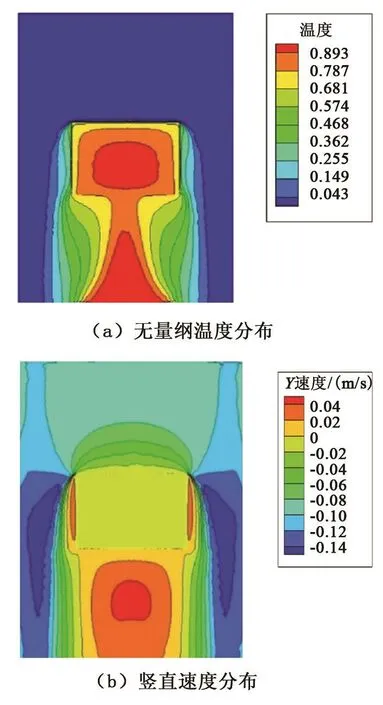
图5 试件模型在降温2 h后过中轴线Y-Z截面上无量纲温度分布与竖直方向上流体流动速度分布Fig.5 Dimensionless temperature distribution and vertical velocity distribution on theY-Zmiddleplane after cooling for 2 h

从图5（b）中看出，相较于空箱下低温流体较为稳定的从进口向出口流动，当有试件模型存在时，上端面出现滞止区，低温流体在此堆积聚集，导致对流效果大大减弱。而在底面局部区域内流体流动速度方向翻转，出现回流现象，这使得出口处于环境温度的流体流入试验箱内，占据了底部区域，高温流体的侵入导致试件模型与流体间温度差减小，对降温过程产生抑制作用。因此，试件模型各处降温速率呈现上述现象。基于以上对试验箱内流动结构及降温性能的分析，以上述工况为基础，对热循环系统中不同结构参数（试件模型离箱底高度、形状及流体送入方式）进行仿真计算，研究不同结构参数对试件模型降温过程的影响，进而达到优化参数目的。

2.1 试件模型离箱底高度对试验箱内降温速率及温度分布的影响

从图5可以看出，由于试件模型对气流的阻挡作用，试验箱体底部出现高温回流区域从而减缓了降温进程，而试件模型与试验箱底部的距离影响着回流区的位置及大小。因此为了研究试件模型离箱底高度对试验箱内温度场的影响，在维持上述工况的送风温度、送风速度及水平位置一致，以0.5 m为间隔，改变模型的竖直位置，即模型底面距试验箱底的高度D，获得的试件模型无量纲平均温度随时间的变化曲线如图6所示。从图中可以看出，随着降温过程的进行，试件模型无量纲平均温度逐渐降低。当D≤4.0 m时，降温末期试件模型无量纲温度基本处于稳定状态，在24 h内无法完成降温过程。当D=4.5 m时，降温时间缩短至12 h。固定降温时间纵向比较可以看出，随着离地高度的增加，模型降温速率逐渐加快，完成降温所需的时间也逐渐减少。

图6 离箱底高度对试件模型无量纲平均温度的影响曲线Fig.6 Effect of the distance between the model and the test chamber bottom on dimensionless average temperature of the model

图7（a）、（b）分别为降温2 h时过中轴线Y−Z截面的温度与竖直方向流体流动速度分布情况。从图7（a）中可以看出，随着试件模型离箱底高度的增大，其底部流体温度逐渐降低，高温区域截面形状由方形逐渐变为锥形直至消失。从图7（b）可以看出，试件模型底部回流区域随试件模型离箱底高度的增大逐渐上移，这使得参与回流的流体由出口处常温流体变为实验箱体内低温流体，这在一定程度上加快了试件模型底部的换热进程，提高了整体降温速率。当D≤4.0 m时，试件模型底部存在高温区域，随着降温过程的进行，高温区域与试件模型及模型内流域间形成了较为稳定的温度梯度，此时对流与导热对试件模型温度的影响愈加微弱，降温过程基本停滞，因此出现图6中降温末期温度基本不变的情况。

图7 降温2 h后试件模型不同离箱底高度时过中轴线Y-Z截面的无量纲温度分布与竖直方向上流体流动速度分布Fig.7 Dimensionless temperature distribution and vertical velocity distribution on the Y-Z middleplaneat different distances after cooling for 2 h

图8（a）、（b）分别为试件模型离箱底高度对无量纲温度极差及无量纲温度标准差影响随降温时间的变化曲线。从两图的对比可以看出，无量纲温度极差与无量纲温度标准差的变化趋势基本一致。

图8 试件模型离箱底高度对无量纲温度极差和无量纲温度标准差的影响Fig.8 Effect of the distances between the model and the test chamber bottom on dimensionless temperature difference and dimensionless temperature standard deviation of the model

当D＜4.0 m时，无量纲温度极差与无量纲温度标准差均随着时间的推进逐渐增大，最终趋于一稳定值。当D>4.0 m时，无量纲温度极差与无量纲温度标准差呈现先增大后减小的趋势，这是由于在降温初期试件模型外壁与低温流体通过对流迅速换热使得试件模型表面温度降低。同时试件模型的壁厚使得冷量无法快速到达试件模型内壁，内壁面温度降低速率低于外壁面，导致试件模型不同时刻无量纲温度极差逐渐增大，无量纲温度标准差随之增大；随着降温过程的进行，试件模型外壁面温度基本降至入口温度，冷量逐渐传递到试件模型内壁面，使得无量纲温度极差与无量纲温度标准差逐渐减小，温度均匀性得到改善。而当D=4.0 m时，图8中曲线呈现出上述两种情况的结合，出现先增大后减小而后增大至一稳定值的情况。降温初期，试件模型底部锥形高温区域未完全形成，对试件模型降温的影响弱于低温流体与试件模型的对流换热，使得初期温度均匀性变化趋势与D=5.0 m时相似；随着降温过程的进行，底部高温区域对降温影响越来越大，成为影响降温速率的最主要因素，温度均匀性曲线则向另一种情况靠拢。

综合以上分析可以看出，随着试件模型离箱底高度的增加，参与回流的流体中低温流体比重逐渐增大，回流区域的平均温度降低，降温速率逐渐增大，温度均匀度也有所改善。从整个研究过程可以发现，改变试件模型的离箱底高度只是改变回流区域位置，并没有改变其大小。

2.2 试件模型形状对试验箱内降温速率及温度分布的影响

从上文仿真计算结果可以看出，试件模型的存在使得流场中出现了滞止区与高温回流区域等流动结构，增大试件模型离箱底的高度只是改变了回流区域的位置，无法影响其大小，而试件模型的形状对流场分布尤其是回流区域的分布会产生一定的影响，因此在基本工况基础上，为了研究不同试件模型高径比对试验箱内温度场及流场分布的影响，在保持入口流体温度与速度不变的情况下，将试件模型固定在试验箱体中同一高度，通过改变试件模型的高径比来研究不同试件模型形状对降温过程的影响。通过计算高径比AR=0.5、1、1.5、2四种情况，得到如图9所示的不同时刻试件模型无量纲平均温度及最大无量纲温度标准差变化规律。

图9 不同降温时间下试件模型高径比AR对无量纲平均温度和无量纲温度标准差的影响曲线Fig.9 Effect of the different aspect ratio on dimensionless temperature difference and dimensionless temperature standard deviation of the model

从图9（a）可以看出，在降温初期，随着试件模型高径比的增大，试件模型的无量纲平均温度呈现逐渐减小的趋势。随着降温过程的继续进行，不同高径比间无量纲平均温度差距逐渐缩小，AR=2时的降温速率始终最快。至降温末期，尤其在AR≥1时同一降温时间试件模型的无量纲平均温度几乎相同。在降温初期当AR=2.0时，试件模型对入口低温流体的阻碍作用明显小于其他高径比，入口低温流体能最大程度地通过对流与试件模型进行换热，加快了降温初期的降温速率。随着降温过程的进行，大高径比带来了回流区域位置的下移，这对降温产生了不利的影响，AR=2.0时降温速率逐渐减缓，与其他高径比间无量纲平均温度的差异也进一步减小。从图9（b）可以看出，无量纲温度标准差的变化趋势与无量纲平均温度有所不同。对于同一降温时间，随着试件模型高径比的增大，无量纲温度标准差呈现先减小后增大的趋势，其中AR=1时试件模型的无量纲温度标准差最小。对于不同降温时间，AR=0.5的试件模型无量纲温度标准差均大于其他高径比。这是由于当AR=1时，试件模型有着最大的比表面积，与低温流体的接触面积最大，冷量能更均匀地从各个方面向试件模型传递，这在一定程度上改善了试件模型降温过程中的均匀性。当AR=0.5时，试件模型有着最大的底面面积，这压缩了低温流体在水平方向上的流通面积。因此，一方面试件模型阻碍了大量低温流体通过，使其在试件模型上面形成滞止区，减缓了试件模型底面的降温速率；另一方面，流通面积的压缩加快了试件模型侧面附近的低温流体竖直方向的流动速率以及侧表面的换热速率。两方面的影响使试件模型径向降温速率大于轴向降温速率，这种降温速率的不同使降温过程中试件模型的温度均匀性变差，使得AR=0.5时拥有着最大的无量纲温度标准差。

图10（a）、（b）分别为不同高径比试件模型在降温2 h后过中轴线Y−Z截面上的温度及竖直流体流动速度分布。从图10（a）中可以看出，不同高径比下试件模型及其内流域的无量纲平均温度分布差异不大。随着试件模型高径比的增大，模型底部流体区域的无量纲平均温度逐渐减小。从图10（b）中可以看出，随着试件模型高径比的增大，回流区域的位置逐渐下移，面积逐渐减小。当AR=0.5时，回流区域拥有最快的回流速度。这是因为AR=0.5时回流区域位置较高，因此在回流区域中的流体多为入口流入的低温流体。低温流体的参与加快了试件模型底部流体区域的降温，使得AR=0.5时试件模型底部流体区域的温度最低。随着试件模型高径比的增加，试件模型的高度越来越高，其底部回流区域距离出口越来越近，这种距离的缩短使得参与回流的流体中出口处流体比例增大，因此对试件模型底部流体区域的降温带来了一定的不利影响，导致了底部流体无量纲平均温度的升高。

图10 不同高径比试件模型降温2 h后过中轴线Y-Z截面的无量纲温度分布与竖直方向上流体流动速度分布Fig.10 Dimensionlesstemperature distribution and vertical velocity distribution on the Y-Z middleplane with different aspect ratio after cooling for 2 h

综合以上分析可以看出，随着试件模型高径比的增大，一方面试件模型对于流动的阻碍作用逐渐减小；另一方面试件模型底部回流区域温度逐渐增大。在二者的综合作用下，降温过程速率逐渐增大，但当AR≥1后，降温速率基本稳定。不同于降温速率的变化，温度均匀度先有大幅改善而后缓慢变差。在高径比增大的过程中，回流区域面积有所减小，但仍然存在。

2.3 流体出入方式对试验箱内试件模型降温速率及温度分布的影响

通过上述对试件模型离箱底高度与高径比的研究发现，无论试件模型形状、位置如何变化，当采用上进下出的方式时，低温流体必然受到试件模型上底面的阻挡，不可避免地导致了滞止区与回流区域的出现。为避免高温回流区的产生，采用不同的流体出入方式对试件模型降温过程进行仿真计算。在维持上述工况的流体送入温度与送入速度的情况下，将试件模型固定在试验箱体中心处，改变试验箱体的流体送入方式，将流体出入口由竖直方向转变为水平方向，即将流体出入由上下布置改为侧面布置，由此计算不同方式下的降温特性，得到图11所示降温曲线。可以看出，当流体侧面出入时试件模型可以在24 h之内完成降温过程。当流体侧面送入时降温过程进一步缩减到了7 h，模型的降温速率大幅度加快。相对于将流体出口布置在侧面，将流体入口布置在侧面时提高降温速率的效果更加明显。当流体入口布置在侧面时，流体出口的位置对降温速率几乎没有影响，两种情况下几乎同时完成降温过程。

图12（a）、（b）分别为不同流体的出入方式下降温2 h后过中轴线Y−Z截面上的无量纲温度及竖直流体流动速度分布。从图12（a）中可以看出，当采用流体侧面出入时，试件模型与试验箱底部间不再存在高温区域，使得试件模型底部与低温流体直接接触，加快了降温进程，使试件模型内部无量纲温度明显低于流体竖直送入方式下无量纲温度。

图11 流体送入方式对试件模型无量纲平均温度的影响曲线Fig.11 Effect of the different airflow patterns on dimensionless average temperature of the model

图12 不同的流体出入方式下降温2 h后过中轴线Y-Z截面无量纲温度与竖直方向流体流动速度分布Fig.12 Dimensionless temperature distribution and vertical velocity distribution on the Y-Z middleplane with different airflow patterns after cooling for 2 h

从图12（b）中可以看出，流体侧面出入口的加入增加了试验箱内流场的复杂程度。当采用流体上进侧出时，在模型底部形成面积巨大且速度较快的回流区域，但此时由于流体送入方式的改变，试验箱体底部为封闭表面，高温流体无法进入试验箱内，参与回流流体为箱体内低温流体，流体回流时与底面进行换热反而提高了降温速率。相对于上部送入，流体侧面送入时的流场分布更为复杂。由于流体入口布置在侧面上部，流体入口处速度为水平方向，因此图中未能显示流体流入速度，但在流体入口下方壁面处形成小区域涡流。从12（b）最后两张图中看出，采用流体侧面送入方式时，几乎在试件模型外表面都产生了涡流，涡流内流体为试验箱内低温流体，相对于流体上进侧出时在底部形成的回流，流体侧面进入时在外表面四周都能形成涡流，这大幅加快了低温流体与试件模型外表面的对流换热，加速了降温进程，使降温时间从13 h减少到7 h，节约了46%的时间。由于流体侧面进入时试件模型周边都参与对流换热，因此流体侧面进入的温度均匀性也好于上部进入。对比后两张图还能看出，流体侧进侧出方式下，模型周边的回流区域要大于侧进下出方式，因此其降温速率略快于流体侧进下出方式，温度均匀性也有较大幅度的提升。

从对上述不同流体送入方式下的仿真计算结果分析可以看出，流体送入方式的改变带来了回流区域位置、数量及大小的改变。在上进下出方式下，回流区域对降温过程有阻碍作用，而当采用流体侧面出入时，由于流体出入口对流体流动方向的改变，回流区域内流体温度接近于其入口温度，且在诸多区域尤其是试件模型外表面附近产生较大速度的涡流，加快了降温过程的进行。因此，从流体送入方式角度考虑，侧进侧出方式具有最好的降温性能，侧进下出次之，再次为上进侧出，上进下出的降温性能最差。