双折射干涉法测量透射相位

2021-02-02张冉冉谭永炎

青岛科技大学学报（自然科学版） 2021年1期

李杨,张冉冉,谭永炎,2,王霞*

(1.青岛科技大学a.数理学院;b.山东省新型材料与技术工程实验室,山东青岛266061;2.香港科技大学物理系,香港999077)

当一束单色光在各向同性介质(例如空气和玻璃)的界面折射时,折射光线只有一束,而且遵循折射定律。但是,当光束入射到各向异性介质时,在介质内会产生两束折射光,这种现象叫做双折射(Birefringence)[1-2]。双折射是由材料的各向异性特性引起的,关于光学频率上的双折射,最有名的例子就是方解石晶体的双像实验,是由丹麦科学家BARTHOLIN 于1669 年首次提出的[1]。1941 年,JONES[3-4]提出:琼斯矩阵是描述偏振器件光学特性的便捷数学工具,可以用2×2矩阵描述偏振元件的特性。1968年,KORMER 指出通过测量测量材料的透射和反射特征可以用来表征晶体的双折射。几十年来,研究者依然多是采用这种方法来测量双折射晶体的双折射特性。1999 年,ABDULHALIM[5]准确的给出了透射和反射传输中的2×2 矩阵。因此,样品的双折射性质可以通过琼斯矩阵进行推导。基于琼斯矩阵原理,ZHANG 等[6]根据双折射晶体的双折射特性,在圆偏振光测量体系中,用无透镜偏振光显微镜对双折射滑膜液晶体进行广域成像,实验成功演示了其在诊断痛风中的应用。最近,ZHOU 等[7]在双折射干涉仪中研究了光子的干涉特性,并且用于表征双折射晶体的温度色散特性。双折射晶体中有一个(或两个)特殊的方向,当光在晶体中沿此方向传播时,不发生双折射,晶体内这个特殊的方向称为光轴。当光在晶体中垂直于光轴传播时,会产生振动方向互相垂直的两折射光。TILLEY 等[8-10]的研究表明,如果用检偏器来检测,这两个不同方向的折射光均为线偏振光。如果投影到同一平面上,则两偏振光频率相同,光矢量(即电场强度矢量E)的振动方向相同,并且在相遇处两光束的相位差恒定,满足干涉条件。2019 年,NORBERT 等[11]指出通过分析在偏振光屏后观察到的干涉图样,即可分析双折射材料中双折射色散和相位双折射色散。本研究通过自主搭建线偏振光测量系统,实验测量了双折射干涉现象,并通过拟合透射光谱的峰/谷求得双折射晶体引入的透射相位。建立琼斯矩阵,理论分析了双折射干涉原理及其透射相位。

1 双折射晶体

最典型表征的双折射材料是晶体,因为晶体具有特殊的晶体构型,相应的折射率可以被很好的定义。蓝宝石(sapphire)是一种氧化铝(α-Al2O3)的单晶[12]。蓝宝石单晶的光学穿透带很宽,从近紫外光(200 nm)到中红外线(5μm)都具有很好的透光性[13],也因此成为本研究的首选研究对象。蓝宝石双折射晶体中包含C,A,M,R4个晶面,如图1所示[14],晶面指数分别为(0001),(110),(100),(101),由于晶体性质随晶面的不同而不同,应用时必须认真考虑晶体的切割方向,本实验选择晶面与光轴平行的A-平面蓝宝石作为研究对象,购买于合肥安中晶体材料有限公司,详细见参考文献[14]。

在A-平面蓝宝石晶体中[15-16],两束折射光线中有一束折射光线始终遵循折射定律,即不论入射光束的方位如何,这束折射光线总是在入射面(入射光线和界面法线决定的平面)内传播,并且折射角的正弦与入射角的正弦之比等于常数,把这束折射称为寻常光折射率,用符号o表示,折射率记为no。而另一束折射光则不然,这束折射光往往不在入射面内,不遵循折射定律,因此,称为非寻常光,用符号e表示,折射率记为ne[17]。在A-平面蓝宝石晶体中折射率大小满足方程(20 ℃,λ＝0.2μm 至λ＝5.5 μm 波段)[18]。

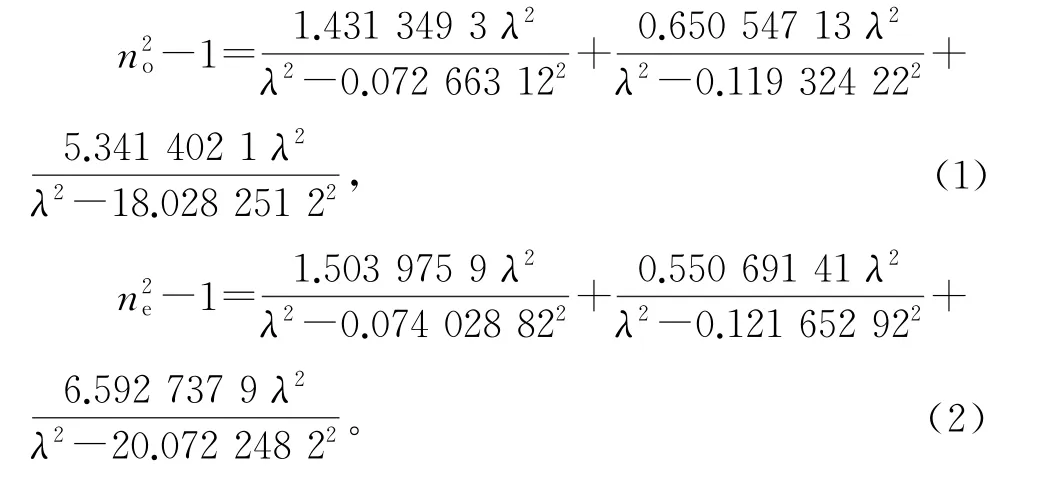
图1 蓝宝石晶体中的不同晶面[14]Fig.1 Different crystal ographic planes of sapphire crystal[14]

2 实验测量

图2为自主搭建的光学测量装置示意图。显微镜选自OLYMPUS 公司奥林巴斯BX6,光谱仪选自美国的OCEAN OPTICS 公司的海洋光学USB4000光纤光谱仪,光谱仪的探测信号通过USB接口传送到计算机。入射光源为显微镜中的卤素灯,可以看作是自然光入射,自然光经过起偏器(PI)后转变为线偏振光,经蓝宝石晶体后光的偏振态发生变化,最后经过检偏器,只有特定方向的偏振光可以经光纤光谱仪传送至电脑被记录下来。左下方插图为测量原理图,α和β表示偏振片的偏振方向,其设定均以x轴方向为参考;定义逆时针方向为正,顺时针方向为负,θ是蓝宝石的光轴与x轴方向的夹角。该测量系统操作简单,灵敏度高,可广泛应用于局部微区测量。

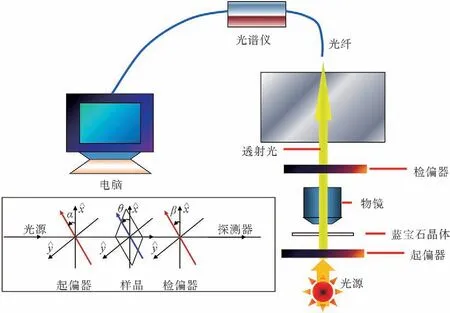
图2 透射光谱测量原理图Fig.2 Schematic setup for transmission measurement

图3为线偏振光(x/y)入射测量蓝宝石晶体透射相位的原理图,箭头0表示入射光束,箭头2表示出射光束,晶体内部由光束1表示,虚线分别表示寻常光1o和非寻常光1e,是振动方向互相垂直的两种偏振态。光轴箭头表示蓝宝石晶体的光轴方向,L表示蓝宝石晶体的厚度。

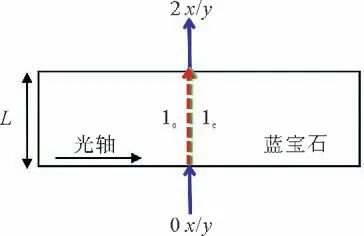
图3 o光和e光的实例分析Fig.3 Illustration of different o-and e-rays

图4为偏振光入射蓝宝石晶体的透射光谱。由实验测量原理图(图2所示),当α＝0～90°,β＝0～90°时,可以容易测得蓝宝石晶体4个方向的透射光谱,即T xx,T yy,T xy,以及T yx,如图4(a)所示,右下方插图为两个周期的放大图。但受显微镜数值孔径(NA)的影响,如果在测量原理中直接加入数值孔径参数,干涉强度分布复杂[19],将难以根据测得的数据直接拟合出相位,另外系统的实际有效数值孔径也难以确定。但若不考虑数值孔径效应,则只能得到相对相位[20],针对这一问题,参考文献[21],综合考虑系统数值孔径和色散等因素,引入波数校正因子

其中λNA表示显微镜的测量波长,λ0表示校准后的测量波长。拟合结果如图4(b)所示,插图为拟合误差。如图4(c)为通过确定校正因子后f,右下方插图为两个周期的放大图,对实验结果得到的峰值波数进行校正后的透射光谱,与校准前相比较有较小移动,如图4(d)所示,以T xx透射光谱为例,实线表示显微镜直接测得干涉光谱,虚线表示校正后的干涉光谱。

3 理论计算

实验中,蓝宝石双折射晶体(厚度为d)垂直于z轴放置,设线偏振光垂直入射(Φ＝0),其振动方向与光轴的夹角为θ,则二维空间的旋转矩阵

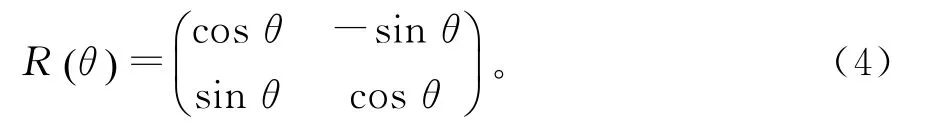
入射光束进入波片后,平行光轴的光波成为e光,垂直光轴的光波成为o光。由于o光和e光在波片内的传播速度不同,穿过波片后,产生确定相位差,记为

图4 蓝宝石透射光谱及分析数据Fig.4 Transmission spectrum of sapphire and analysis data

则蓝宝石双折射晶体的琼斯矩阵可写为

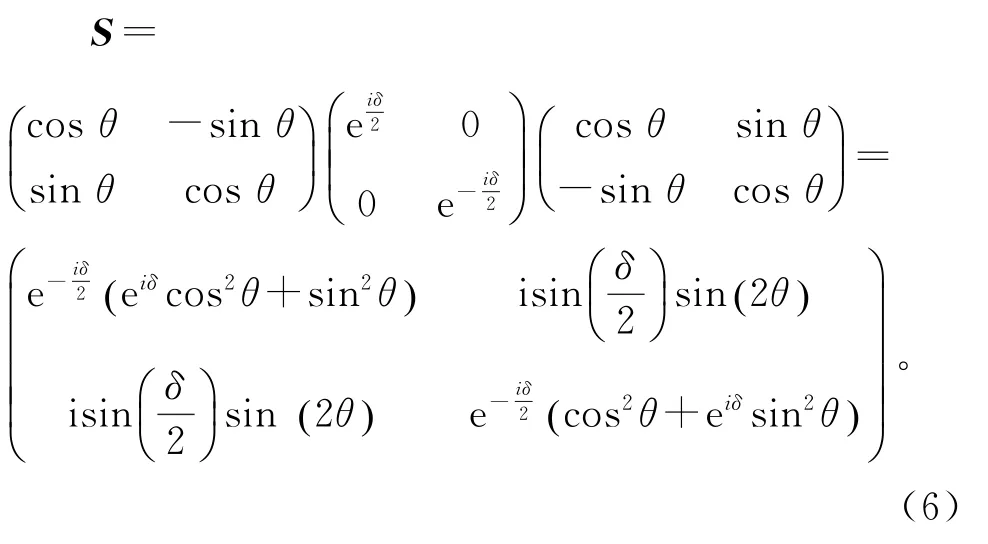
矩阵S即为双折射晶体在线性空间中的琼斯矩阵。实验中,设定θ＝45°,则双折射晶体的琼斯矩阵可以表示为

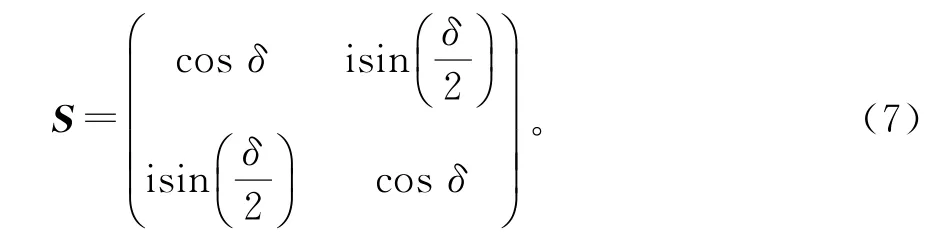
假设有一束单色平面波沿z轴传播,其电场强度的琼斯矢量为

其中E ij为电场强度的复数表达,下角标i表示出射光,j表示入射光。E x0,E y0为两个复数分量,分别表示入射光束沿x,y方向的电场矢量。结合方程(7)可得出射光波电场强度的琼斯矢量:

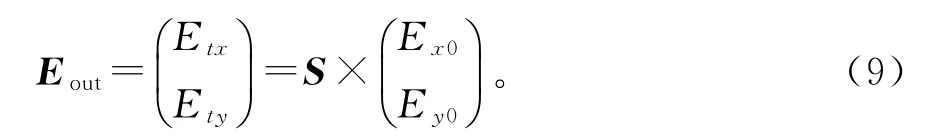
其中,E tx,E ty为两个复数分量,分别表示出射光束沿x,y方向的电场矢量。当光矢量沿x轴入射时,E x0＝1,E y0＝0。则有

对应的电场强度为

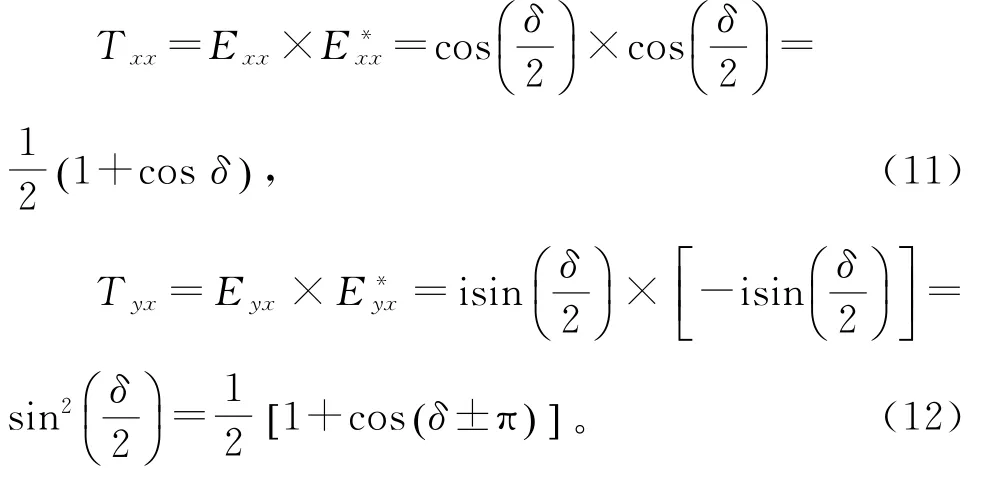
同理,当光矢量沿y轴入射时,E x0＝0,E y0＝1。则有

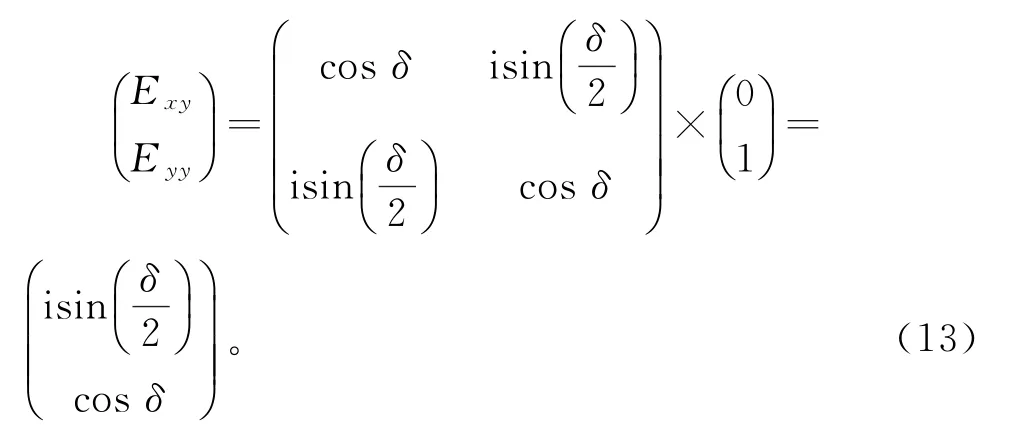
对应的电场强度为

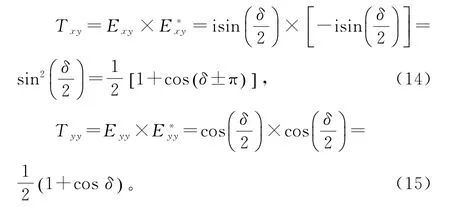
式(5)代入公式(11)、(12)、(14)、(15)可得双折射晶体的4个方向的透射光谱,即T xx,T yy,T xy,以及T yx,如图5(a)所示。图5(b)为实验测量结果与理论计算结果的对比图,以T xx方向的透射光谱为例,实验结果与理论计算结果高度一致。

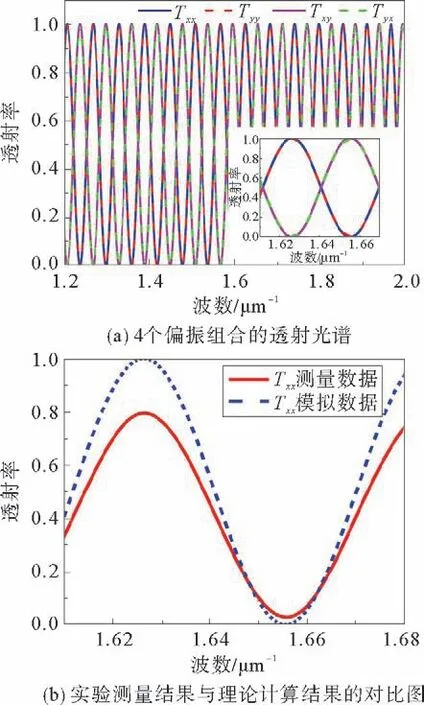
图5 实验结果与理论计算对比图Fig.5 Comparison figures between experiment and simulation

图6为T xx对应的干涉级数m与相应的波数,由双光束干涉模型可知,双折射晶体中,o光和e光干涉相长时满足

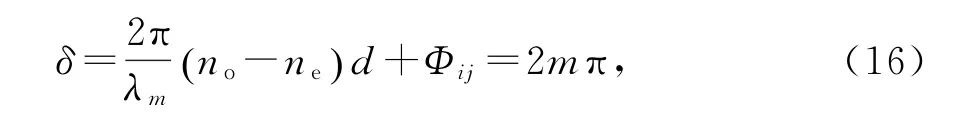
其中,λm为双折射晶体中第m级干涉级数对应的波长,d为o光和e光在晶体中的光程。Φij为双折射晶体的相位,对应于方程(11)、(12)、(14)、(15),Φij＝0或±π(等式右边加π即为o光和e光干涉相消)。等式(16)等价于

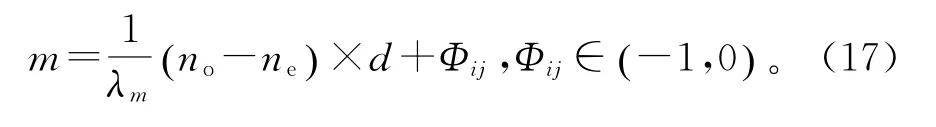
由公式(17)可知,m与成线性关系,因此,通过Origin拟合,即可求得蓝宝石晶体的透射相位。图6右下方的插图为拟合误差,表明拟合效果较好。

图7为蓝宝石晶体的透射相位。

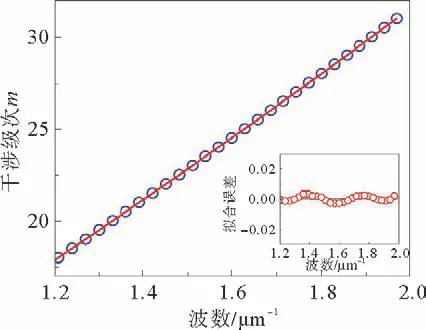
图6 T xx对应的线性拟合结果及拟合误差Fig.6 Linear fitting results of T xx and the residuals of the fitting

图7 实验测量与理论计算数据的比较Fig.7 Comparison of experimental measurement and theorical calculation data

图7(a)为实验测量结果的拟合数据,图7(b)图标为理论计算结果的拟合数据,实线及虚线为理论分析结果,即－1或－0.5(除以2π作归一化处理)。Φ＝－1表示同方向的透射相位,双折射晶体没有引入透射相位值;Φ＝－0.5 表示交叉方向的透射相位,因入射光束偏振方向与出射光束的偏振方向垂直,故引入π的相位差。实验测量结果与理论计算结果高度一致。