基于混合激活函数的改进卷积神经网络算法

刘国柱,赵鹏程,于 超,王晓甜

(青岛科技大学 信息科学技术学院,山东 青岛266061)

卷积神经网络是一种典型的多层前馈人工神经网络。激活函数则是人工神经网络模型中不可缺少的重要组成部分。通常在大多数人工神经网络中所使用的激活函数多为Sigmoid、Ramp(ReLU)、Tanh等单调、非周期性的非线性函数。并且在多层卷积神经网络中,通常都会使用同一种激活函数,而几乎不会同时使用多种激活函数。大多数人并不认可Sinusoid函数作为神经网络中激活函数的能力,因为它并不单调。而早 在1987 年,LAPEDES 与FARBER 首 先 成 功地建立了使用Sinusoid函数作为激活函数的具有一个隐藏层的神经网络[1]。他们将此解释为广义的傅里叶分解。最近的一个研究工作中,GASHLER 和ASH MORE 在深度神经网络中使用了Sinusoid,Linear和ReLU 函数作为激活函数用于预测时间序列数据[2]。ALEXANDER、MAXIMILIAN 和ALEXANDER 在简单进化网络(evolving parsimonious networks)中使用了混合激活函数[3]。而在卷积神经网络中使用Sinusoid函数作为激活函数进行图像分类任务以及在卷积神经网络中使用混合激活函数的有关工作尚缺乏。

本研究将Sinusoid(Sin)函数作为激活函数引入到多层卷积神经网络中,建立了一个使用混合激活函数的多层卷积神经网络模型,并在图像分类任务中对其收敛速度和识别效果进行了研究。另外,也将该模型同其他研究者所使用的一些图像分类算法在分类效果上进行了对比。

1 模型建立

提出一个使用混合激活函数的卷积神经网络模型。作为对照,在保持神经网络的基础结构不变的情况下,分别将每个神经网络中各单元所使用的激活函数替换为其他4种激活函数中的同一种函数,建立其他4个神经网络模型。

1.1 激活函数

对于使用任意有界、连续的非常数函数作为激活函数的标准多层前馈神经网络而言,HORNIK 的研究表明通用逼近理论[4]仍然适用。只要在输出有界的情况下,这类网络能够以任意精度逼近任何实值连续函数[5-6]。

因此激活函数的具体选取,理论上不会影响神经网络的表达能力。

函数Sinusoid:f(x)＝sin(x)为在实数域上连续有界的非常数函数。在多层卷积神网络中使用Sinusoid激活函数是可行的。

基于相关工作和理论基础[1-6],在构建的5 个卷积神经网络模型中使用了4种激活函数,如图1所示,分别为Sinusoid:f(x)＝Sin(x),Ramp:。

图1 神经网络所使用的4种激活函数:Sinusoid,Ramp,Sigmoid,TanhFig.1 Four activation functions used in neural networks:Sinusoid,Ramp,Sigmoid,Tanh

1.2 LeNet-5基本结构

由LECUN 等[7]提出的Le Net-5是一种已经被广泛使用的经典多层卷积神经网络模型。该网络原始结构如图2所示,不包括输入层其总共有7层,其输入数据为大小32×32×3的图像。其第1层为卷积层,卷积核大小为5×5;第2层为池化层,采样区域大小为2×2;第3层为卷积层,卷积核大小为5×5;第4层为池化层,采样区域的大小为2×2;其他层为全连接层。该网络在第1层与第2层之间、第3层与第4层之间和第5层与第6层之间全部使用Sigmoid激活函数。

1.3 模型修改

S-S-R LeNet-5:以原始LeNet-5 为基本结构,如图2所示,将其中第4、第9节点所使用激活替换为Sinusoid函数,将第15节点替换为Ramp函数。

Ramp LeNet-5:以LeNet-5 为基本结构,将第4、第9和第15节点全部替换为Ramp函数。

Sinusoid LeNet-5:以Le Net-5 为基本结构,将第4、第9和第15节点全部替换为Sinusoid函数。

Tanh Le Net-5:以LeNet-5 为基本结构,将第4、第9和第15节点全部替换为Tanh函数。它们的网络层次结构依次如图3所示。

图2 LeNet-5网络结构Fig.2 LeNet-5 network structure

图3 S-S-R LeNet-5,Ramp LeNet-5,Sinusoid LeNet-5,Tanh LeNet-5网络结构Fig.3 S-S-R LeNet-5,Ramp LeNet-5,Sinusoid LeNet-5,Tanh LeNet-5 network structure

2 实验与结果分析

2.1 数据集

本研究中所使用的数据集为CIFAR-10[8]数据集和MNIST 数据集。

其中,CIFAR-10数据集在图像分类任务中被广泛使用。它包括了10类共60 000张大小为32*32的彩色图片,每个类有6 000张图片。其中训练集包括50 000张图片,测试集有10 000张图片。该数据集中所包含的图片分为Airplane、Automobile、Bird、Cat、Deer、Dog、Frog、Horse、Ship、Truck 共十类。

MNIST 数据集是一个公开的手写数字数据集,该数据集由一个具有60 000个样本的训练集和一个具有10 000个样本的测试集组成。样本的标签值为0到9的10个数字,共10类。该数据集中每一个样本均为大小为28*28的灰阶图片。

2.2 实验环境

实验设备所使用的中央处理器为Intel(R)Core(TM)i7-7700 HQ＠2.80 GHz;内存大小为8 GB;图形处理器为NVIDIA GeForce GTX 1050Ti;实验设备使用的操作系统为Windows 10专业版操作系统。

2.3 模型训练

以S-S-R LeNet-5混合激活函数卷积神经网络为实验模型,用其他4个模型作对照。对于上述的每一个模型,均使用ADAM[9]优化算法来训练,5个神经网络模型全部采用随机初始化方法进行权重初始化。

在验证图像分类任务中混合激活函数卷积神经网络S-S-R Le Net-5模型的分类精度和收敛速度优势的实验中,将使用CIFAR-10数据集来训练5个模型,训练模型时,将使用CIFAR-10数据集中训练数据集的所有图片样本,批处理大小均设为64,总训练次数为6次。底层使用MXnet深度学习框架进行训练和评估。

在验证图像分类任务中混合激活函数卷积神经网络S-S-R LeNet-5模型的分类精度同其他研究者的分类算法相比具有竞争力的实验中,将使用MNIST 数据集中训练集的所有60 000个样本来训练S-S-R LeNet-5模型。本实验使用的优化算法同上一个实验保持一致,总训练次数修改为35次。由于MNIST 数据集中的训练样本数量比CIFAR-10数据集中的训练样本数量多10倍,为了提高模型的训练速度,本实验将批处理大小修改为5 000,以加速模型的训练过程。

2.4 结果与分析

为了比较使用混合激活函数的卷积神经网络S-S-R LeNet-5模型和使用单一激活函数的卷积神经网络模型在图像分类任务中识别准确率以及收敛速度的表现,实验设置了Sigmoid LeNet-5、Tanh LeNet-5、Ramp LeNet-5、Sinusoid Le Net-5共4种使用单一激活函数的卷积神经网络模型作为对照模型。表1展示了上述5种神经网络模型在CIFAR-10数据集中测试集上的识别准确率。

表1 各模型在CIFAR-10测试集上的分类精度Table 1 Classification accuracy of each model on the CIFAR-10 test set

表1中的数据可以表明,同Ramp LeNet-5模型和Tanh LeNet-5模型相比较,S-S-R LeNet-5模型的识别准确率分别提高了1.52%和1.78%,而与Sigmoid LeNet-5模型相比,其分类准确率要高14.44%。同其他4种模型相比,S-S-R LeNet-5模型的识别准确率指标均有显著提高,且S-S-R LeNet-5模型具有最高的图像识别准确率,达到了68.04%。

上述实验结果和分析表明了使用混合激活函数的卷积神经网络模型在图像分类任务中的识别准确率具有明显的提升。同时该实验从另一个方面表明,激活函数的类型是神经网络在图像分类任务中识别准确率指标的重要影响因素,在保持神经网络基本结构不变的条件下,仅通过改变激活函数的组合,使用混合激活函数即取得了更高的识别准确率。

另外为了比较上述5种模型的收敛速度表现,验证使用混合激活函数的卷积神经网络S-S-R LeNet-5模型具有更快的收敛速度,对5种模型在CIFAR-10数据集上的训练过程进行了统计和分析。

对于深度神经网络模型而言,模型在训练阶段的学习曲线(包括训练识别错误率学习曲线、训练损失学习曲线两种)表现了在训练过程中相应模型的收敛速度。本实验中5种模型的训练识别错误率学习曲线和训练损失学习曲线结果分别如图4和图5所示。此外,统计了5种神经网络模型的总训练时间、最终训练损失和最终训练准率,结果如表2所示。

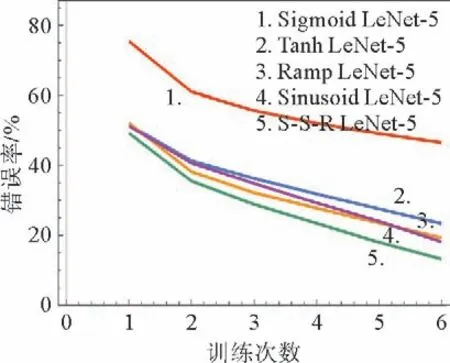
图4 5种网络分类错误率随着训练次数的改变情况Fig.4 Five networks classification error rates change with the number of training times

图5 5种网络训练损失随着训练次数的改变情况Fig.5 Five networks training cost change with the number of training times

表2中的数据表明:在相等的27 s总训练时间里,5种模型中使用混合激活函数的卷积神经网络S-S-R LeNet-5模型所取得的最终训练损失最低,达到了0.372 7;取得的最终训练准确率最高,达到了92.54%。另外结合图4与图5所示的两种学习曲线进行分析可知,使用混合激活函数的卷积神经网络S-S-R LeNet-5模型在5种模型的训练过程中具有最快的收敛速度。相比于其他4种使用单一激活函数的卷积神经网络模型,其训练过程中的收敛速度具有较大提升。

表2 各模型的总训练时间、最终训练损失和最终训练准确率Table 2 Classification accuracy of each model on the CIFAR-10 test set

值得注意的是,从上述两个实验的结果中可以发现,使用Sinusoid LeNet-5模型在图像分类任务中的识别准确率和训练收敛速度方面,同其他使用经典激活函数的卷积神经网络模型相比,取得了较为优秀的表现。实验数据验证了Sinusoid函数作为神经网络激活函数使用的可行性。

最后,为了验证S-S-R LeNet-5 模型在其他图像分类数据集上同样有有效,且在识别准确度指标上同其他研究者的分类算法相比具有竞争力,在MNIST 数据集上重新初始化并训练了S-S-R LeNet-5模型。在MNIST 数据集上进行图像分类的算法有许多种,选取了反条纹支持向量机(IFSVM)[10]、多层感知机(MLP)[11]、一种著名的深度卷积神经网络(Alex Net)[12]、模糊受限玻尔兹曼机(FRBM)[13]4种算法在MNIST 测试数据集上同SS-R LeNet-5模型就分类准确率指标进行对比,其中IFSVM 算法的分类结果来自参考文献[13],其他3种对比算法的分类结果来自参考文献[14]。上述各算法在MNIST 测试数据集上的分类准确率如表3所示。

表3 各模型在MNIST测试集上的分类精度Table 3 Classification accuracy of each model on the MNIST test set

通过分析表3中的有关数据,使用混合激活函数的卷积神经网络S-S-R LeNet-5模型在MNIST测试数据集上达到了99.20%的分类准确率,高于其他4种对比算法。该实验验证了S-S-R LeNet-5模型同样适用于其他图像分类数据集,且相比于其他研究者的算法,本模型在图像分类准确率指标方面具有竞争力。

3 结 语

使用混合激活函数的卷积神经网络模型S-S-R LeNet-5模型在图像分类任务中的识别准确率达到了68.08%,明显高于其他4种使用单一激活函数的卷积神经网络模型;使用混合激活函数的卷积神经网络模型S-S-R LeNet-5 具有更快的收敛速度,在训练集上取得了更高的识别准确率;图像分类实验初步验证了在多层卷积神经网络中使用Sinusoid函数作为激活函数的可行性,实验数据表明Sinusoid LeNet-5模型相较于使用传统激活函数的Sigmoid LeNet-5模型,在图像分类任务方面具有更高的准确率;同其他研究者的工作进行对比,虽然使用混合激活函数的卷积神经网络模型初步展现出有竞争力的精度优势,但在其他任务中该类模型的性能表现有待进一步研究,未来的工作方向可探索此类模型在回归任务上的表现。