绕圆柱非定常尾涡对液滴碰撞聚结影响的数值模拟

李 涛,金睿珠,谭更彬,刘宇飞,曹 兴,王志泉

(1.青岛科技大学 机电工程学院,山东 青岛266061;2.山东省思威安全生产技术中心,山东 济南250014)

在油包水型乳化液的破乳过程中,主要通过施加外部干扰因素,使液滴的运动状态以及界面膜发生相应的变化,以此来促进液滴之间的碰撞以及迅速聚结,目前电脱水法是应用最广泛的一种脱水方式[1-2]。ATTEN[3]和THORODDSEN 等[4]提出在油脱水过程中,加入气体吹扫装置来产生剪切层的方式产生剪切力且增加乳化液的流动性。有研究发现,湍流和剪切力可以促进水滴相互靠近同时也能抑制链的形成[5-7]。BAILES等[8]运用喷射气泡的方法来强化脉冲电场中液滴的相互作用。FRIEDEMANN 等[9]将剪切力和电场力共同作用于乳化液,发现分离效率有显著提高。SQUIRES等[10]证明液滴会积聚在涡流中高湍流度区域,使液滴间碰撞概率增加。MELHEIM 和FENANDEZ[11-13]分别研究了不同含水率、不同电导率乳化液在剪切流和电场共同作用下的分离效果,得出剪切流有利于提高液滴电聚结效率的理论,同时强调过大的剪切流会造成已经形成的大液滴再次发生破裂的情况,并得出湍流强度是实现液滴碰撞的重要参数,较弱的电场仅仅辅助了聚结过程的结论。刘忠等[14-15]、赵盛清等[16]对超细颗粒物的聚结以及在双圆柱绕流中颗粒物的团聚进行模拟,得到绕流对颗粒团聚的影响。张书斌[17-18]发现圆柱和涡片组合而成的新型湍流聚结室对颗粒物湍流聚结效果有明显的增强效果,在此基础上进一步探究出圆柱绕流中产生的涡流可以促进流场中小颗粒的聚结。李岩[19]发现流场速度、颗粒体积分数会影响颗粒间的聚结效果。刘含笑等[20]利用模拟分析对比不同的圆柱排列情况对颗粒聚结的影响,并得出最佳位置。

目前,国内主要对液滴聚结中电场的类型及电场强度进行探究,剪切流对液滴聚结效率的影响的理论研究没有深入探索。圆柱绕流是指当流体绕流圆柱时,会出现边界层分离、旋涡脱落等一系列的复杂且存在一定规律的物理现象,本研究中引入圆柱绕流,使流场中湍流度增大的同时产生剪切力[21-23],以此来提高液滴聚结效率。利用有限元分析软件对乳状液在圆柱绕流作用下多物理场的运动过程进行模拟,探究圆柱绕流对液滴聚结效率的影响,主要研究不同入口速度分布、速度大小、液滴相对位置下,液滴的变形及聚结情况。

1 数学模型

1.1 几何模型及边界条件

将模型简化为二维层流两相流的模型,如图1所示。模型简化为在矩形区域中连续相为油,分散相是水。左边界为入口,右边界为出口。在入口处设置半径为R＝6 mm 的固定圆柱,根据文献[24],取圆柱与大液滴之间的中心距L1＝5R;两水滴的半径分别为R1＝2 mm,R2＝1.5 mm。为保证模拟结果的稳定性,模型的入口处、上下边界与圆柱的中心距离设置为10D[25](D为圆柱直径),同时为保证液滴变形过程的充分性,设置出口边界与柱体的中心距离为40D。

图1 二维模型示意图Fig.1 Schematic diagram of two-dimensional model

1.2 液滴对中心夹角定义

液滴对的中心夹角是以大液滴的圆心为顶角,以穿过大液滴圆心的水平线为基准线,以两液滴圆心的连线为另一条线,两条线所形成的夹角为液滴对的中心夹角,图1为液滴对中心夹角为α的模型。无论液滴对中心夹角怎样变化,其液滴对圆心之间的距离L2始终为10 mm。

1.3 流场参数

模拟过程中,水相和油相的物性参数如表1所示。根据文献[26],定义迁移参数表达式如式(1)所示,油水界面张力系数为0.031 N·m－1,设置环境温度为25 ℃。

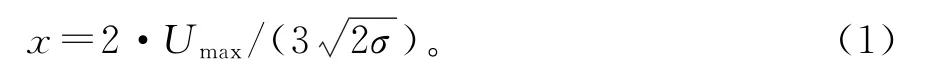
表1 水滴和油相的物性参数Table 1 Physical properties of water droplets and oil phases

1.4 流场控制方程

层流两相流相场接口,根据N-S方程设置流体运动方程:

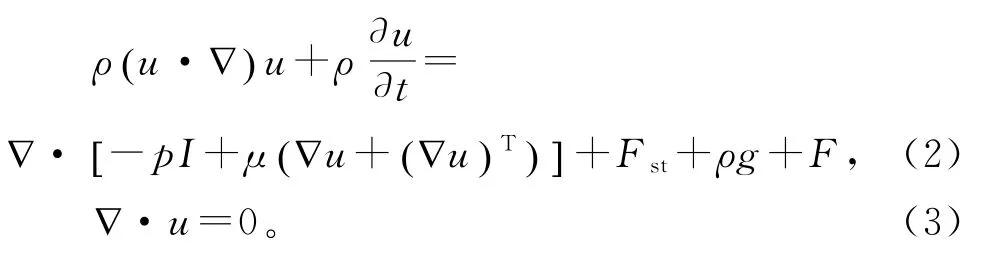
为了跟踪层流两相流的流体界面,相场接口使用相场方法(Cahn-Hilliard):

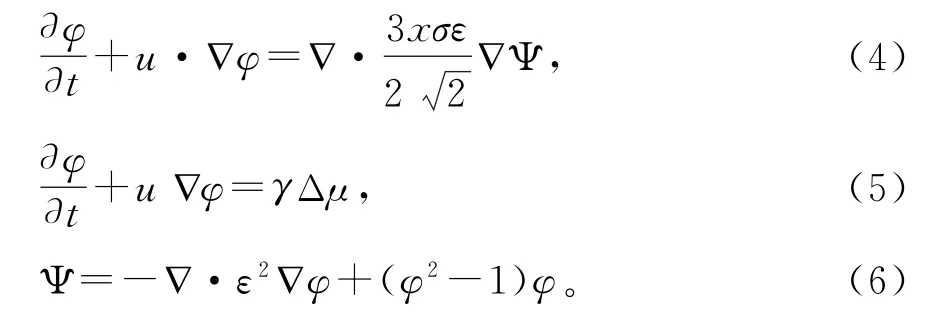
相场法是通过相场变量φ来得到界面层的信息,而不是直接追踪两种流体界面的变化。相场法将表面张力等效为场变量的梯度和化学势的乘积,并将其作为一个体积力加入到N-S方程中。通过偏微分Cahn-Hilliard方程来控制相场变量的演化。而利用Cahn-Hilliard方程,相场界面被分解成2个2阶的偏微分方程,这样就保证了在整个领域保持质量守恒。即在整个数值计算过程中不仅可以计算流体界面的对流,同时可以保证系统的总能量合理减小,尤其适合两种互不相溶流体的系统。

1.5 速度场控制

根据牛顿内摩擦定律,由于流体的黏性作用,在层流中摩擦阻力及沿程水头损失均与流速成比例关系。当流速充分发展后的分布呈抛物线型,为更好地将模拟结果贴近于实际应用,引入抛物线流速方程,设置抛物线型入口流速。图2为平均速度为2 m·s－1的入口速度分布示意图。入口速度分布为抛物线型流场称为工况1,即流体充分发展后再进行圆柱绕流,设置其速度表达式为v＝6y(1－y)(y为模型入口纵向坐标,v为入口y坐标处的速度);入口速度分布为均匀流场称为工况2。

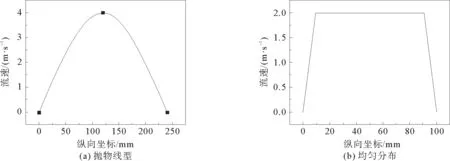
图2 入口速度分布Fig.2 Inlet velocity distribution

图3为两种入口形式下绕圆柱尾流区域形成的流场速度分布图。从图3看出,不同入口形式对尾流区漩涡脱离的频率和周期有着重要影响,当雷诺数Re不大于40 时,圆柱尾流为附体的两个对称涡,为定常解。当Re大于40后流动为非定常及非对称的,圆柱尾流呈现周期性涡旋交替脱落而形成卡门涡街。如图3所示,在工况1流场中,圆柱后方形成交替分布的涡,同时在涡集中分布区域的流速明显大于流场设定的均匀流速,且在涡分布的周围,流速能达到3.0 m·s－1,在工况2中未形成交替分布的涡,只是在圆柱后方有涡的脱落,在涡的附近流场流速能达到2.5 m·s－1,而其他区域的流速仅仅在2.0 m·s－1左右徘徊。

2 结果与讨论

2.1 入口速度分布对液滴变形影响

图4是在没有圆柱的纯流场中,入口速度为抛物线流型,平均流速是2.0 m·s－1的液滴对的变形过程。由图4看出,液滴对形变幅度小并且大约在0.15 s发生碰撞,图5中在相同速度、流型的绕流场作用下液滴对产生形变且碰撞的时间在0.01 s。在绕流场作用下,液滴的聚结效率明显提高。

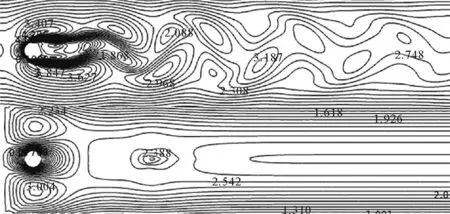
图3 流场速度分布图Fig.3 Velocity distribution of flow field

图4 纯流场中抛物线流型液滴变形过程及压力分布Fig.4 Deformation process and pressure distribution of parabolic droplet in pure flow field

图5 是在中心夹角0°,平均流速是2.0 m·s－1,入口速度分布分别是抛物线型和均匀型的流场中液滴对在0.01、0.05、0.09、0.15、0.20 s时刻的变形聚结特征以及流场中的压力、流速分布图。在开始的0.01 s时刻,工况1中的两液滴的左侧发生轻微的拉长变形且发生碰撞聚结;工况2中的大液滴呈月牙状,小液滴拉长呈椭圆状,但液滴对之间未发生碰撞聚结。经过0.04 s运动,工况1中液滴对已经聚结完成,且聚结形成的大液滴轮廓较圆滑;而工况2中的液滴对发生碰撞聚结,但大液滴未融合完全,大液滴左侧有一处凹陷,右侧的拉伸现象明显,形成类心形的大液滴。在0.09 s时刻,工况1中的液滴对碰撞聚结后形成的大液滴已经完成融合且轮廓曲线圆滑,大液滴的轮廓形状稳定;工况2中的液滴对碰撞聚结后形成的大液滴进一步融合,右侧拉伸幅度减小,左侧凹陷幅度减小,轮廓更加圆滑。在0.15 s后,工况1中的大液滴形变成心形且在随后时间变化中形变稳定;工况2中的大液滴不断发生微弱形变,右侧不断缩短,左侧凹陷程度小幅度增加,液滴融合度较差。在0～0.20 s过程中,从液滴对的聚结角度看,工况1中液滴对的聚结时间比工况2的聚结时间提前,即工况1的聚结效率比工况2的聚结效率高。工况1在0.01 s时,圆柱后侧产生少量涡的脱落,在0.05 s时,圆柱后侧涡量增多且涡变大,在流场充分发展0.09 s时间后,在圆柱两侧形成交替脱落的涡且涡的数量不断增多,涡的尺寸不断增大,流场中流速明显提高,使圆柱后侧流场的扰动性不断增大;工况2中只在圆柱后侧形成少量的涡且没有形成交替脱落的涡,圆柱后流速变化幅度较小,对圆柱后侧流场的扰动性较小。因此,入口速度分布对分散相液滴的变形及聚结时间产生了显著的影响,工况1中的大液滴比工况2中的大液滴轮廓更圆滑且稳定度更高,液滴聚结的效率也更高。在剪切力、黏性应力以及界面张力的作用下,液滴逐渐形成一个具有一定变形率的大液滴,在工况1场中,液滴对聚结后,逐渐稳定成心形大液滴,在抛物线型流场中,液滴对发生碰撞的时间比工况2短,且液滴聚结后逐渐稳定成圆滑的心形大液滴。因此,工况1比工况2更有利于液滴的聚结。

图6为流场中最大涡量的变化曲线,涡量是流体有旋性的特征量,其值越大流场的扰动性越强。由图6看出,在液滴变形的时间段内,工况1中流场的最大涡量约为工况2的3.5倍,可知工况1中流场的旋涡强度远大于工况2中的旋涡强度。

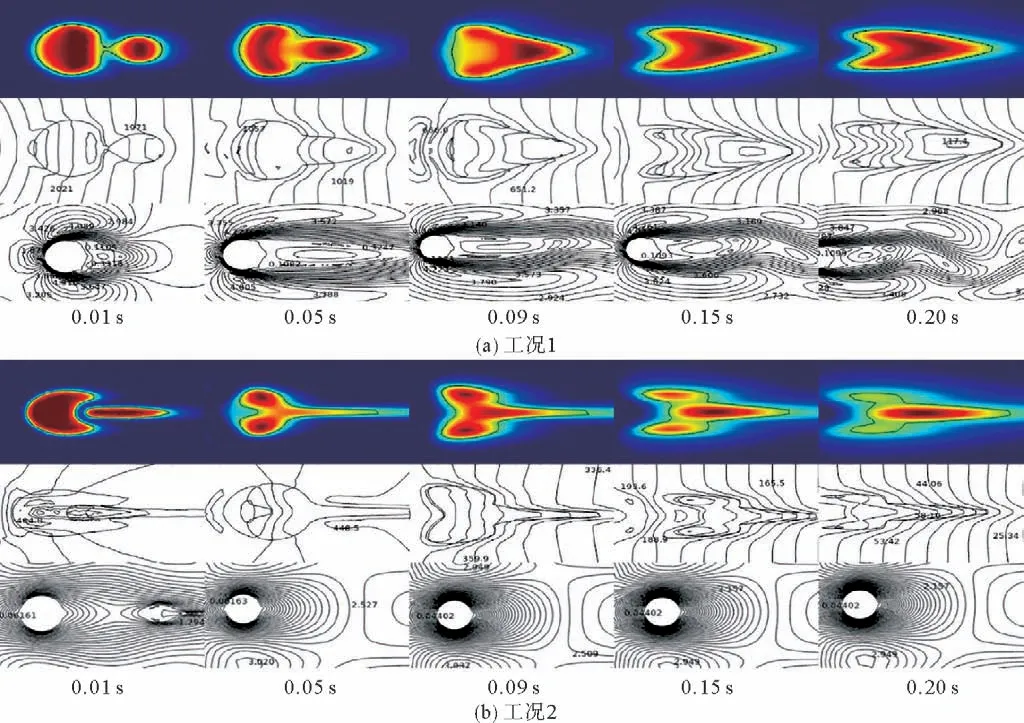
图5 圆柱绕流中不同流型下液滴变形过程及压力分布Fig.5 Droplet deformation process and pressure distribution under different flow patterns in cylindrical flow

图6 流场中最大涡量变化Fig.6 Maximum vorticity variation in the flow field

图7为在速度为2.0 m·s－1的圆柱绕流过程中,工况1和工况2流场中的最大流速随时间的变化曲线,在圆柱绕流中,最大流速一般出现在柱体的涡脱落边界。由图7中可以看出,工况1的最大流速始终大于工况2的最大流速。

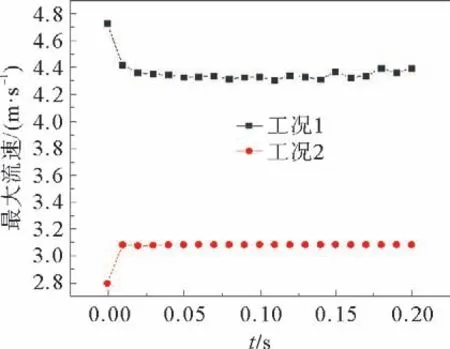
图7 流场中最大流速变化Fig.7 Maximum velocity change in a flow field

在液滴变形过程中,液滴都是在靠近圆柱的一侧先发生变形。随后在不断运动的过程中,液滴会向着轴向两侧拉长的趋势变形成椭圆形,但是在工况1场中,聚结后的大液滴会从类三角形液滴变形为心形液滴,而工况2中的大液滴缓慢变形且形状不规则。这是由于在圆柱绕流中,流体流经圆柱体后会形成压力不相等的区域,根据相对于圆柱体的位置将其分为前端压力区、两侧压力区和背压区。如图5所示的压力等值线图,液滴靠近圆柱的一侧压力最大,随着与圆柱距离增大,压力越来越小,液滴的两段形成压力差。在工况1中液滴两端的压力差大致在40～50 Pa之间,工况2中压力差大致在30～40 Pa之间。液滴在流场中受到压力差的作用,液滴先发生左侧拉长变形,液滴对之间左侧距离逐渐减小。当液滴对聚结后,液滴在流动过程中受到错落分布的旋涡的影响,大液滴在黏性应力及剪切力等外力作用下,发生变形。

因此,结合图4、5可得,圆柱绕流可以提高液滴对相互碰撞的效率。在圆柱绕流中,流体流过圆柱时会产生边界层分离,旋涡脱落,脱落的旋涡会随着流体的流动在流场中错落分布,这些涡会增强流场中的扰动性同时对流场中的液滴产生剪切力作用。结合图5、6、7分析可得,工况1中最大流速、最大涡量都大于工况2,因此工况1中的扰动作用大于工况2,涡的强度和流场中的湍流强度越大。因此,油相中的液滴随着流场中的旋涡流动而受到旋涡的剪切力作用,变形程度增大,进而增加液滴对的碰撞效率。工况1产生的涡量比工况2多,工况1中流场的扰动性比工况2大,液滴对受到旋涡剪切作用也大,从而工况1液滴对的碰撞聚结效果比工况2好。所以工况1的聚结效率比工况2的聚结效率高。

2.2 流速对液滴变形影响

对工况2中心夹角为0°的液滴对在不同的流速下的运动特征进行模拟研究,考察速度大小对液滴聚结效率的影响,结果见图8。

图8 0°夹角液滴对在工况2中碰撞时间随进口速度的变化Fig.8 Impact time of droplet pairs with an Angle of 0°varies with inlet velocity in working condition 2

从图8中可以观察到,速度越大,聚结时间越短。在相同时间点时,不同流速的液滴对聚结情况不同,在t＝0.05 s时,速度为0.5和1.0 m·s－1的液滴对之间距离减小但未发生聚结,但速度大于2.0 m·s－1的液滴对分别发生不同程度的聚结。由此可见,流速增大使液滴对的聚结时间缩短,但在不同的流速范围内,影响的程度不同,如速度由0.5 m·s－1增大至1.0 m·s－1时,液滴对的聚结时间由0.12 s缩短到0.05 s,聚结效率提高约60%,但在流速从1.0 m·s－1增大至3.0 m·s－1的过程中,聚结时间仅缩短0.03 s,聚结效率一共提高约50%,且在流速提高至2.5 m·s－1以后,聚结时间没有发生较大差异。这是由于流体绕流圆柱,流速越大,所产生涡的脱落频率越高,对液滴的作用性也越强。但是尾迹中涡的数量会随离圆柱距离的增大而减弱,当流速越来越大时,液滴的运动速度也会随流体的速度增大,使液滴位置距圆柱越来越远,所受到涡的作用力不会产生明显差异,因此随着流速增大,液滴的聚结效率会降低,甚至液滴的聚结时间不会产生较大差异。因此,流速对液滴对的聚结过程有促进作用但不是均匀的。

图9显示不同流速下,液滴变形聚结的过程。

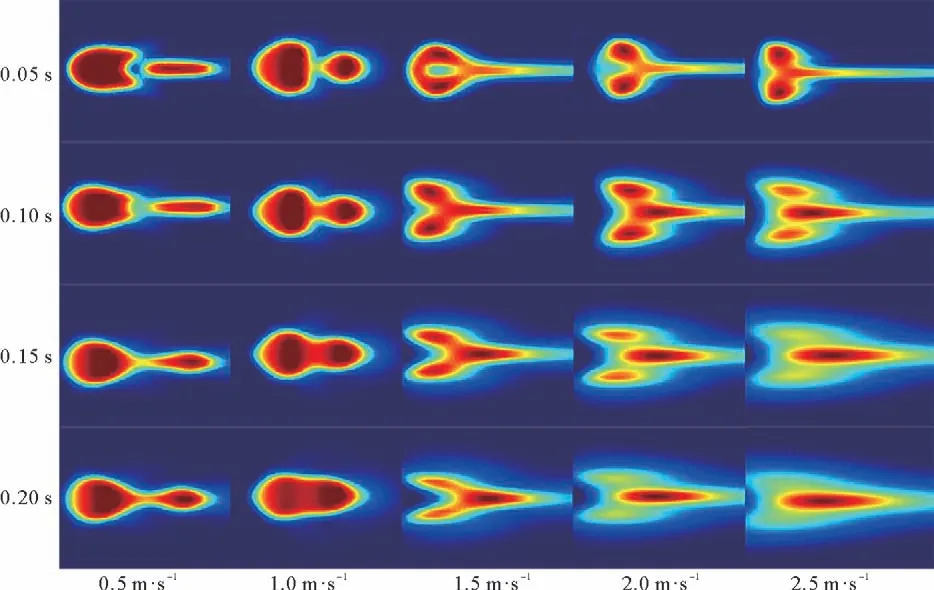
图9 不同流速下液滴对的变形聚结过程Fig.9 Deformable coalescence of droplet pairs at different flow rates

由图9看出,液滴的变形趋势是横向轴逐渐拉长,但在不同的流速中,液滴拉长的程度不同,且聚结后,液滴稳定成大液滴的形状也各有差异。当t＝0.05 s时,速度为0.5 m·s－1的液滴对中,中、小液滴变形为细长条形,大液滴由于受到压力差的作用发生向左凹陷状变形。随着速度的增大,当速度增大到1.5 m·s－1时,液滴受到尾迹旋涡以及流场作用力,大液滴左侧受到冲击,左端发生向右侧凹的变形,随着速度的增大,尾迹的旋涡对液滴的作用减弱,大液滴逐渐稳定为心形。液滴的变形趋势不同,同时变形的速度也有差异,由图9可以看出:随着速度的增大,液滴的变形速度也越来越快,大液滴形状稳定所需时间也越来越短。当速度为0.5 m·s－1时,液滴经过0.2 s的运动,只发生初步聚结作用,大液滴的变形趋势还未显示,当液滴增大到1.0 m·s－1时,液滴经过0.1 m·s－1的运动已经变形为轮廓较光滑的椭圆形,在0.20 s时刻,大液滴向着椭圆形稳定。而速度为1.5 m·s－1时,液滴在0.10 s时刻已经完成聚结且大液滴形状已经稳定。由于尾迹旋涡分布差异的影响,流场中速度增大到2.0和2.5 m·s－1时,聚结形成的大液滴变形需要在0.15 s时刻稳定下来,虽然作用减弱,但其聚结变形效果比速度为1.0 m·s－1时好。

由以上分析可以得出:流场速度对液滴的变形、碰撞、聚结以及大液滴形状稳定都有影响。在尾迹涡流的影响下,液滴的变形、碰撞、聚结以及形状稳定都随着速度的增大其促进效果越来越强。

2.3 液滴相对位置对液滴变形的影响

在油水乳状液中,水相以水滴的形式随机分散在连续的油相中,由于液滴形状的对称性,在圆心距不变的情况下,从0°～90°范围内选取4个不同的角度作为液滴对的中心夹角来探究液滴的相对位置对液滴发生碰撞聚结过程的影响。本研究中选取的4个角分别为0°、30°、45°、90°。

图10是液滴对在平均速度为0.5 m·s－1,入口速度分布为抛物线型的圆柱绕流中,不同相对位置的液滴对发生的形变。图11是不同中心夹角α下,液滴对在不同速度的碰撞时间。结合图11、图10可以看出:在圆柱绕流中,分散相液滴随中心夹角α增大,绕流场对液滴对的作用力逐渐减小。在t＝0.1 s时,随着α的增大,液滴的聚结效率不断降低,液滴对发生碰撞聚结所需时间不断增加。这是因为在相同的流场中,随着液滴对夹角的不断增大,液滴对所受到剪切力的作用逐渐减小,液滴的变形程度逐渐减小,液滴对的聚结效率也逐渐减小,在相同的时间点,液滴越不容易接触。显然,夹角α越小的液滴对越容易发生碰撞聚结。当t＝0.15 s时,α＝0°的液滴对已经完成聚结,α＝30°的液滴对已经接触刚发生碰撞,而α＝45°、α＝90°的液滴对没有发生碰撞聚结。图10中t＝0.20 s时,只有α＝90°的液滴对出现变形未发生碰撞聚结效应。在液滴对发生聚结后,大液滴在剪切力及黏性应力的作用下,液滴逐渐聚结为椭圆形大液滴,如图10中t＝0.45 s所示,α＝0°夹角时,液滴稳定为轮廓圆滑的圆形,但随着夹角的不断增大,大液滴稳定时的轮廓与圆形差异越来越大,当增大到45°时,液滴最终稳定成顶角具有弧度的长方形。可见,绕流产生的错落分布的旋涡可以缩短液滴对之间的距离。但是当液滴对中心夹角α增大到一定值时,剪切力及黏性应力对液滴对的作用大大削减,使液滴对无法完成碰撞聚结。

图10 不同相对位置下液滴变形特征Fig.10 Droplet deformation characteristics at different relative positions

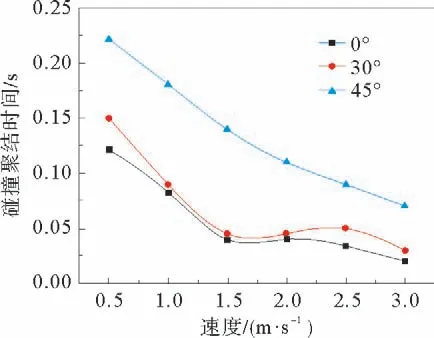
图11 不同夹角下液滴对的碰撞聚结时间Fig.11 Collision coalescence time of droplet pairs at different angles

3 结 论

1)圆柱绕流的尾流产生的剪切力对乳化液液滴之间的变形与聚结有促进作用,在相同流速、流型下,在绕流作用的流场中液滴对发生聚结所需时间缩短为无绕流作用的流场的时间的1/15。

2)入口速度分布类型和流速都会影响液滴的变形以及液滴对的聚结效率。抛物线型比匀速型更加促进液滴对的聚结效率,在均匀流速相等工况中,抛物线流型流场中液滴对发生聚结所需时间是均匀型流场的1/5。在液滴对相对位置及流型相同的条件下,流速越高液滴对发生聚结的效率越高,均匀流速每增大0.5 m·s－1,液滴对发生聚结所需时间缩短1/5左右;液滴的拉伸效果也越强,在均匀流速从0.5 m·s－1增大到2.5 m·s－1过程中,液滴由圆形横向拉伸为类椭圆形,且类椭圆形的长短轴之比由4.77增大到8.00。

3)液滴对的相对位置对液滴对的聚结也产生影响。当液滴对相对夹角在0°～45°范围内,液滴对的聚结效率随夹角的不断增大而降低,液滴间的夹角每增大15°,液滴发生聚结所需时间延长0.1 s,当液滴间夹角为90°时,液滴不会在短时间内发生碰撞聚结,且形成的大液滴的形状也越来越不规则,稳定时的形状从椭圆形过渡到心形且液滴稳定所需时间越来越长。

符 号 说 明

Umax——流场中最大迁移调整参速度,m·s－1;

σ——界面张力系数,N·m－1(本研究用油水界面张力系数,取定值0.031 N·m－1);

u——速度,m·s－1;

ρ——密度,kg·m－3;

μ——动力黏度,Pa·s;

p——压力,Pa;

g——重力加速度,m·s－2;

I——单位张量;

Ψ——相场辅助变量;

Fst——表面张力,N·m－1;

F——任何附加体积力;

ε——流体界面厚度的数值参数,m;

Ф——相场变量,当值为1时表示油相,值为－1时表示水相。