压制观瞄系统多光谱光轴平行性调校技术研究
2014-03-27孙毓凯刘召庆王小怡
孙毓凯,刘召庆,王 晶,王小怡
(1. 总参陆航部装备发展办公室,北京 100012; 2. 西安应用光学研究所, 陕西 西安 710065)
引言
多光轴光学系统平行性的测试方法有很多种,常见的有:室内测试法、野外测试法、单一系统测试法和组合系统测试法。室内测试法常采用大口径复消色平行光管对光学系统的平行性进行调校和检测,该方法测试原理简单,但大口径平行光管的生产较困难,成本较高。野外测试法(如侦察车的多光轴侦察系统)基本思路是将测角转化为测距,再根据各组合的特点和原理对光轴进行测试,该方法适合(类似装甲侦察车系统)整体测试。单一系统的多光轴测试主要是对激光测距机的三光轴平行性的测试,激光测距机中常通过拨转光学系统的偏心环来实现平行性的校正。组合系统测试是针对单一系统的多光轴测试而言的,一般的测试仪器都是将各光学系统进行机械组合,然后再测试各光轴的平行性[1-3]。针对压制观瞄系统的结构和性质,本文采用双光楔旋转的方法对系统光轴平行性进行调校。
1 系统调校原理
本文涉及的压制观瞄系统具有可见光光轴、激光光轴以及回转机械轴,如图1所示,由于系统基于回转光具座,通过光具座的旋转实现准确对准目标,在保证回转光具座机械轴铅垂的前提下,以铅垂的机械轴为调校的基准,即保证可见光轴、激光光轴与回转光具座的机械轴同心。由于系统结构的特殊性,在生产过程中首先采用摄像机模拟非可见且对人眼有危害的激光器,其次保证回转光具座的铅垂轴与基准摄像机的中心轴同心,即在结构上保证系统机械轴与激光光轴的平行性,所以,系统三轴平行性的调校问题变成了激光光轴与可见光光轴平行性调校的问题[4-5]。
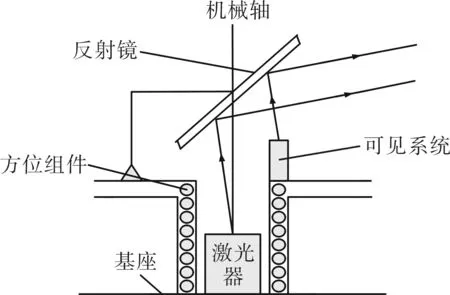
图1 多光谱空间旋转光轴结构示意图Fig.1 Structure diagram of multi-spectral spatial rotary optical axis
双光楔调校方法可以保证可见光轴和激光光轴按图2所示的方向进行校准,光轴垂直入射到双光楔的前一表面后经过一系列的折转,从其后表面出射产生偏向角,从而实现在光路中折转光线的目的,对于偏转角为δ的双光楔,其在光路中的光轴折转如图2所示[6]。

图2 双光楔在光路中的示意图Fig.2 Schematic diagram of dual-optical wedge in light path
图2中的光学系统是压制观瞄系统中电视观瞄具的物镜系统。从光学系统可以看到图3所示的图像,在图3中,K1、K2分别表示第1块和第2块光楔的最厚点,光轴通过第1块双光楔所成像的集合形成Φ1=2δ的一个圆,再经过第2块光楔成像,则是直径为2δ的一个圆周[7]。

图3 从望远镜中看到的图像Fig.3 Image from telescope
如图3所示,假设像点的最后位置是B,它的坐标为(α,β),则K1、K2点与水平轴的夹角是φ1、φ2。像点和原点K1、K2的关系可表示为
(1)
设M=φ1-φ2,可以得到:
(2)
由以上公式可知:当已知被调整的光轴偏角α、β时,通过计算原点K1、K2的位置,再通过电机转动光楔φ1、φ2,主光路将转到α、β位置,利用(1)式和(2)式从理论上计算得到角度φ1、φ2,再旋转光楔,使光轴被调到中心[8]。
2 采用双光楔进行光轴调校的数学模型
根据(1)式、(2)式可知,只要知道光轴偏离中心点的位置(α,β)(在这里以激光光轴的位置为中心建立坐标系,可见光光轴偏离中心的位置即为光轴偏离中心点的位置),就能计算出双光楔转过的角度φ1、φ2,当φ1、φ2得知,通过旋转双光楔相应的角度,就能将光轴的位置向中心点的位置靠近。于是,只要求出φ1、φ2关于(α,β)的函数,通过函数
的计算,就能求出光楔转过的角度φ1、φ2,从而转动双光楔实现对光轴的调整。光轴与中心点的位置关系为
(3)
通过推算可以得出:
当β/α<0时,
(4)
(5)
当β/α>0时,
(6)
(7)
以上所得到的公式是双光楔转动的角度值(φ1,φ2)关于光轴的位置(α,β)的函数,采用Matlab对以上公式进行模拟得到双光楔转动的角度(φ1,φ2)随着光轴位置(α,β)的变化趋势,模拟如图4所示。

图4 双光楔转动角度数学模拟图Fig.4 Analog simulation diagrams for rotation angle of double-wedge
通过以上4幅模拟图可以看出双光楔旋转的角度(φ1,φ2)随着光轴的位置(α,β)的变化趋势。光轴在α2+β2<4δ2区间范围内,当β/α<0时,变化趋势为上两幅图,可以得出随着光轴位置的变化,φ1角在(3.141 4, 6.283 2)mrad范围内变化,φ2角在(7.603 8×10-6, 3.141 8)mrad范围内变化。当β/α>0时,变化趋势为下两幅图,可以得出随着光轴位置的变化,φ1角在(-2.129 1×10-4,3.141 6)mrad范围内变化,φ2角在(-3.141 6, -2.129 1×10-4)mrad范围内变化[9]。
3 实验及数据分析
3.1 双光楔光轴调校实验
双光楔光轴调校的实验装置由大口径平行光管、采用摄像机代替激光器、压制观瞄系统(待调校产品)和双光楔构成。
实验过程如图5(a)所示,可见光系统放在系统上,调整光学实验台瞄准参考光源十字,如果可见光轴与激光光轴平行,参考光源十字成像于摄像机系统,两十字线位置如图5(b),否则,两光轴不平行。

图5 双光楔调校光轴示意图Fig.5 Schematic diagram for collimating optical axis with dual-optical wedge
假设角度偏差量为α、β,图中位移量a、b为角度偏差量α、β在焦面上的位置偏差,则双光楔旋转使偏差量α、β小于0.1 mrad[10]。
3.2 光轴调校方法分析与总结
通过理论计算与实验结果比较验证光轴调校方法的可行性。
1) 理论计算。当光轴被调整到所需位置时,计算双光楔旋转角度。在实验中α=-0.2 mrad,β=-0.2 mrad,δ=0°,
则可计算得到:
2.363 4 mrad
2.346 6 mrad
即第1块光楔和第2块光楔分别旋转2.363 4 mrad和2.346 6 mrad ,使光轴从位置(-0.2 mm,-0.2 mm)转移到中心位置。
2) 实验数据。在实验中,双光楔旋转使光轴从(-0.2 mm,-0.2 mm)转移到(0.025 mm,0 mm),当光轴折转到所需位置时,第1块光楔和第2块光楔分别旋转2.303 mrad和2.285 mrad。
通过理论计算和实验数据,采用双光楔进行光轴调校时,理论所需调校的角度(2.366 4 mrad,2.346 6 mrad)与双光楔实际旋转角度(2.303 mrad,2.285 mrad)的误差量很小,仅为(0.063 mrad,0.061 6 mrad)。
4 结论
根据调校系统的结构特性,采用双光楔旋转的方法对其进行调校,运用双光楔扫描法实现对光轴的偏差调校,通过数学模型的建立和实验的验证,发现双光楔扫描法可以准确、方便地实现对光轴偏差的调整,满足调校激光光轴、可见光光轴、机械轴三轴平行性0.1 mrad的技术指标。
[1] Fu Yuegang,Wang Zhijian,Li Bo. Collimation and test of the multi-spectral optical system parallel[J].Journal of Changchun Institute of Optical and Mine Mechanics,2001,24(4):11-14.
付跃刚,王志坚,李博.多光谱光学系统平行性的调校和检验方法探讨[J].长春光学精密机械学院学报,2001,24(4):11-14.
[2] Zhan Qihai,Chang Benkang,Fu Rongguo. Test equipment of the parallelism of the multispectral optical system[J].Journal of Applied Optics,2005,26(5):25-27.
詹启海,常本康,富容国.多光谱光学系统光轴平行性组合测试装置[J].应用光学,2005,26(5):25-27.
[3] Zhang Jingxian, Li Yudan, Jin Weiqi. Low-light and infrared imaging system[M].Beijing:Beijing Institute of Technology Press,1995.
张敬贤,李玉丹,金伟其.微光与红外成像系统[M].北京理工大学出版社,1995.
[4] Chen wenjian,Zheng Baozhong,Yang jianli. Auto collimation of multispectral multi-optical axis[J].Journal of Applied Optics, 2004,25(1):60-64.
陈文建,郑宝忠,杨建莉.多光谱多光轴自动校准技术[J].应用光学,2004,25(1):60-64.
[5] Fu Rongguo,Chang Benkang,Qian Yunsheng,et al. Optical axis collimation of the laser designation.[J].Optical Technique,2007,33(2):41-43.
富容国,常本康, 钱芸生, 等.激光指示器光轴调校技术[J].光学技术,2007,33(2):41-43.
[6] Kou Xiaoming,Liu Shangqian,Hong Ming,et al. Test of the FLIR performance[J]. Journal of Harbin Institute of Technology,2010(9):52-53.
寇小明,刘上乾,哄鸣,等. 红外热像仪综合性能的客观评价及实现技术[J].哈尔滨工业大学学报,2010(9):52-53.
[7] Han Jun,Wang Jing,Chen Wenjian,et al. The study of the adjustment of the rotate multi-spectral multi-optical axis.[J]. Laser & Infrared,2009,39(4):415-416.
韩军,王晶,陈文建,等. 空间旋转多光谱多光轴校准技术研究[J].激光与红外,2009,39(4):415-416.
[8] Xiang Shiming,Gao Jiaobo,Jiao Mingyin,et al. Modern optic electro image technique[M].Beijing:Beijing Institute of Technology Press,2010,128-193.
向世明,高教波,焦明印,等. 现代光电子成像技术概论[M].北京:北京理工大学出版社,2010.
[9] Ji Ming. Simulation and error analysis of the reflect mirror stabilization system.[J]. Journal of Applied Optics,2000,21(5):19-22.
纪明. 反射镜稳定系统的仿真与误差分析[J]. 应用光学,2000,21(5):19-22.
[10] Zhou Liwei,Liu Yuyan. Target detection and identify[M].Beijing:Beijing Institute of Technology Press,2002.
周立伟,刘玉岩.目标探测与识别[M ].北京:北京理工大学出版社,2002.
