铁路盘型制动噪声机理及其控制方法

乔青峰，杨伟东，朱 琪，陈光雄

（1.中车青岛四方机车车辆股份有限公司技术中心，山东青岛266111；2.西南交通大学机械工程学院，四川成都610031）

随着列车运行速度提高，车辆制动功率也随之增大，现代运行速度V≥120km/h的铁道车辆普遍装备了盘型制动系统.铁路盘型制动系统工作时容易产生制动摩擦噪声，而且有时制动摩擦噪声的声压级达到100～120dB（A），给乘客和铁路沿线居民的日常生活带来了很大的烦扰.解决铁路车辆盘型制动噪声问题，需要认识该种噪声的产生机理:Lorang等[1]研究了法国高速列车的盘型制动噪声问题，发展了一个铁路盘型噪声预测模型，据报道，预测结果与现场实测结果比较一致；Sinou等[2]研究了法国高速列车盘型制动噪声发生机理，研究了影响盘型制动噪声的主要因素.更多的学者研究了汽车盘型制动噪声产生机理[3-5]，认为黏-滑运动（即摩擦力-相对滑动速度负斜率）导致制动摩擦噪声：Spurr[6]认为Sprag-slip引起制动摩擦噪声；North[7]认为摩擦系统的模态耦合引起制动摩擦噪声；Rhee[8]认为摩擦表面之间的微凸体在滑动过程中的锤击作用产生制动摩擦噪声；Mottershead等[9]认为转动盘的双模态分离引起制动摩擦噪声；Chen等[10]认为摩擦力的时滞特性引起制动摩擦噪声.现在，国内外普遍接受模态耦合机理作为制动摩擦噪声机理，近年来国际学术界大量使用的摩擦噪声有限元预测分析就是基于模态耦合机理发展而来[11-16].

本文首先从典型的车辆盘型制动器摩擦噪声的现场测量入手，测量该种制动摩擦噪声的振动和声学信号，获得铁路盘型制动噪声的发生规律；然后建立原型尺寸的铁路盘型制动系统摩擦噪声预测模型，在闸片与制动盘之间的摩擦特性曲线使用实测数据；通过实测制动摩擦噪声与预测制动摩擦噪声的比较，验证了所建立模型的正确性.使用该模型研究各种参数对盘型制动摩擦噪声的影响，提出抑制和消除制动摩擦噪声的方法.

1 制动摩擦噪声现场测试

1.1 测点布置

根据摩擦噪声是制动摩擦系统模态耦合振动发射的特点，在现场测试时只测量闸片托的振动以及盘型制动单元附近的声学信号，闸片托的振动分别测量了法向和切向（摩擦力方向）的振动分量，见图1（a），噪声传声器固定在转向架的构架上，见图1（b）.

1.2 测量仪器

加速度传感器、传声器与B&K噪声信号测试采集系统相连，进行同步数据采集，采样频率为12.8kHz.

1.3 试验工况

分别从列车运行速度30、60、80、100、120、140km/h开始制动直到列车停止为止，在制动过程中分别测量了盘型制动摩擦噪声以及对应的振动.

图1 制动噪声测点布置Fig.1 Measurement positions of brake squeal

2 盘型制动摩擦噪声预测模型

2.1 摩擦系统运动方程

目前国际上预测制动摩擦噪声的常用方法主要是制动系统运动稳定性的复特征值分析法，考虑制动系统闸片和制动盘之间的摩擦耦合作用以后，摩擦系统有可能出现不稳定振动，即不稳定振动的振幅随时间的增加而逐步增大，达到一定数值后就会发射摩擦噪声.在摩擦耦合作用下摩擦系统的运动方程为

判断式（2）是否存在摩擦自激振动的方法通常是对该方程进行复特征值分析，得到摩擦系统的不稳定自激振动频率和振型.式（2）的通解为

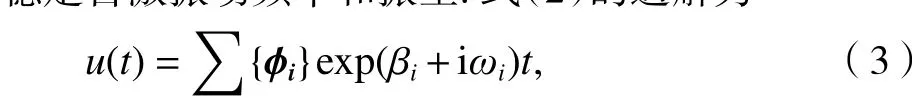
2.2 盘型制动系统摩擦噪声有限元模型

预测制动摩擦噪声的模型通常有集总质量模型和有限元模型，前者只能进行定性分析，不易得到定量的摩擦噪声频率和振型，后者可以比较定量地预测到摩擦噪声的频率和振型.图2是全尺寸盘型制动系统有限元预测模型，用于本论文的盘型制动摩擦噪声定量预测和参数灵敏度研究.在该模型中，所有销连接用无摩擦的接触来模拟，闸片托与闸片摩擦材料之间的连接用tie来模拟.该模型约有108000个节点和 80000个 C3D8I单元.制动盘的弹性模量E1=190.0GPa，密度 ρ1=7300kg/m3，泊松比 ν1=0.27；闸片的弹性模量 E2=1.5GPa，密度 ρ2=2500kg/m3，泊松比 ν3=0.30；闸片托的弹性模量 E3=206.0GPa，密度 ρ3=7800kg/m3，泊松比 ν3=0.30；其它钢材的弹性模量 E4=210.0GPa，密度 ρ4=7800kg/m3，泊松比ν4=0.30.

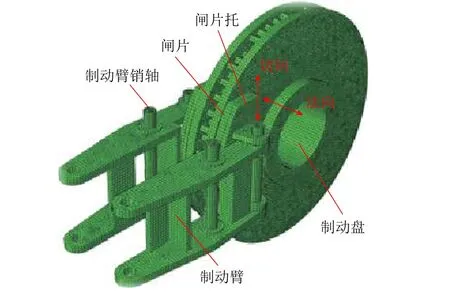
图2 铁路盘型制动噪声预测模型Fig.2 Prediction model of railway disc brake squeal

3 结果及分析

3.1 盘型制动噪声的测量及分析

3.1.1 盘型制动噪声信号分析

图3为盘型制动噪声的测量信号，振动和噪声信号的变化趋势相似，比较图3（a）和图3（b）可以看到，闸片托的法向振动大于闸片托的切向振动，闸片托法向振动最大值是闸片托切向振动最大值的2倍左右，闸片托的法向振动大于切向振动的原因可能是其法向刚度小于切向刚度.

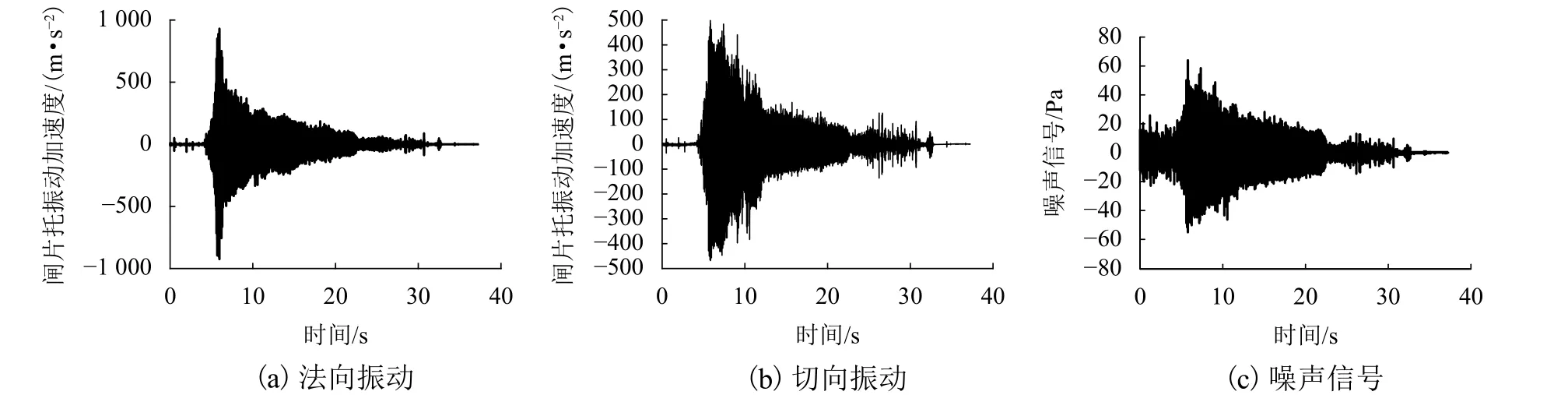
图3 制动尖叫振动和噪声信号Fig.3 Brake squealing vibration and noise signals

图4 为闸片托振动的功率谱.

由图4可知：闸片托法向振动和切向振动的主频与噪声的主频相同，分别为 256.78、3904.07、4320.38Hz；闸片托的法向振动和切向振动的主频相同，说明尖叫噪声发生时闸片托法向振动模态和切向振动模态是耦合的，摩擦系统的模态耦合是引起摩擦噪声的重要原因；噪声信号的主频与闸片托振动的主频相同，说明噪声信号主要是闸片托的振动发射.

图5为闸片托法向振动的时频分析.

由图 5可知：频率为 256.78Hz的振动从时刻 t=6.52s开始且持续到t=22.48s；频率为 3904.07Hz的振动信号从时刻t=6.15s 开始且持续到t=11.84s；频率为 4320.38Hz 从时刻t=5.29s开始且持续到t=7.74s；不同频率的尖叫振动开始和结束时间都有所不同，这可能与制动摩擦界面的摩擦特性的时变特性有关.

图4 尖叫振动和噪声的功率谱分析Fig.4 PSD analysis of squealing vibration and noise

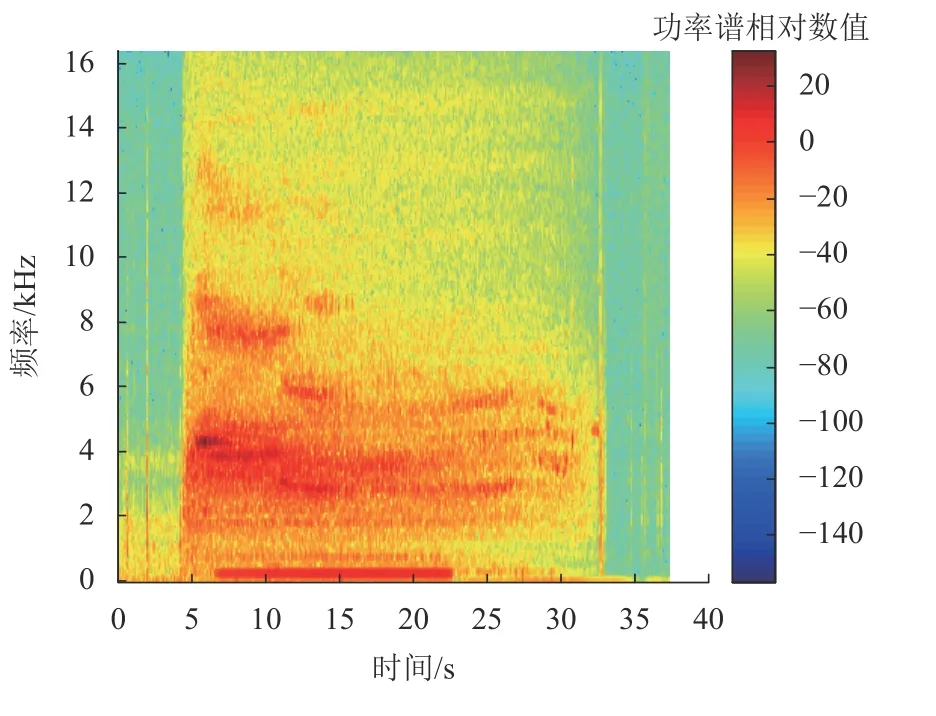
图5 闸片托法向振动的时频分析Fig.5 Time-frequency analysis of the normal vibration of pad bracket

3.1.2 铁路盘型制动噪声的发生规律

铁路车辆有紧急制动、快速复合制动、快速纯空气制动、常用复合制动、常用纯空气制动等5种制动工况.每种制动工况的差别主要是制动缸的空气压力不同，紧急制动的制动缸压力p=460.00kPa（推力F=14917N）、最大常用复合制动的制动缸压力p=311.72kPa（F=10109N）、最大常用纯空气制动的制动缸压力p=398.67kPa（F=12929N）、快速复合制动的制动缸压力p=380.42kPa（F=12337N）、快速纯空气制动的制动缸压力p=464.31kPa（F=15057N）.试验发现，铁路盘型制动噪声的产生有较强的规律性，制动噪声主要发生在最大常用复合制动和快速复合制动这两种工况，如表1所示.由表1可以看出，车辆盘型制动噪声与制动缸的压力有明显的相关性，制动缸压力小的制动容易出现摩擦噪声.

3.2 铁路盘型制动噪声的理论研究

3.2.1 盘型制动噪声的理论预测结果

对图2的盘型制动系统进行有限元复特征值分析可以获得该制动系统的摩擦噪声的特征频率和发生趋势，图6是盘型制动系统摩擦噪声的频率和等效阻尼比分布，与图4实测的不稳定振动频率比较可得：实测振动尖叫振动频率256.78Hz与预测频率292.39Hz之间的相对误差为13.87%；实测振动尖叫振动频率 3904.07Hz 与预测频率 3873.92Hz之间的相对误差为0.70%；实测振动尖叫振动频率4320.38Hz 与预测频率f=4073.32Hz 之间的相对误差为5.72%；由此可见，摩擦噪声的预测结果与实测结果比较一致，低频256.78Hz的预测结果相对误差略大，这是因为预测频率数值较小.

表1 摩擦噪声发生的记录Tab.1 Records of brake squeal occurrence

由图6可知：预测频率f=292.39Hz时的不稳定振动频率对应的等效阻尼比绝对值最大，而且是低频振动，激励需要的能量小，因此该不稳定振动和噪声发生的概率最大，与试验实测的结果一致；模型预测频率f=3873.92Hz的等效阻尼比绝对值比较小但制动时也发生了该模态的振动和噪声，一般来说等效阻尼比绝对值越大就越容易产生摩擦噪声，但也有个别等效阻尼比绝对值较小的模态发生摩擦噪声，这个现象过去也有报道.

图7为3个不稳定振动的模态形状，发生摩擦噪声时，闸片托及闸片的法向振动和切向振动是耦合的，说明模态耦合对此种摩擦噪声的发生有重要的影响.

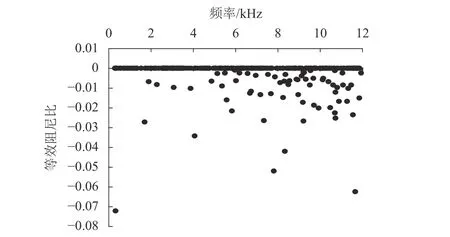
图6 盘型制动系统不稳定振动频率分布Fig.6 Distribution of unstable vibrations of disc brake system

图7 盘型制动器主要不稳定振动的模态形状Fig.7 Mode shapes of several unstable vibrations of disc brake

3.2.2 盘型制动噪声的影响参数研究

3.2.2.1 摩擦系数对制动噪声的影响

不考虑其他输入边界，一般条件下，盘型制动摩擦副摩擦系数随滑动速度的增加而减小，本文以实测的盘型制动器摩擦系数作为模型输入分析摩擦系数对制动器摩擦噪声的影响，图8为摩擦系数对盘型制动噪声的影响，由图8可以看到，盘型制动系统等效阻尼比的绝对值随着摩擦系数的增加而增加，随着摩擦系数的增大，盘型制动系统就越容易产生摩擦噪声.

3.2.2.2 闸片弹性模量对制动噪声的影响

根据《城市轨道交通车辆合成闸瓦技术规范》CZJS/T0012—2016的规定，合成闸片的弹性模量≤1.0GPa.图9为3种不同闸瓦弹性模量对应的制动器摩擦噪声等效阻尼比随制动缸推力的变化，由图9可以看出：闸片弹性模量对制动摩擦噪声有显著的影响，特别是当闸片弹性模量为1.5GPa且F=15.0kN的时候，盘型制动系统的摩擦噪声指标（等效阻尼比的绝对值）最大，达到3.243，此时制动系统很容易产生摩擦噪声；当闸片弹性模量和制动压力不匹配的时候，如 E2=1.5GPa和 F=15.0kN，制动系统的等效阻尼比的绝对值很大，很容易产生摩擦噪声.

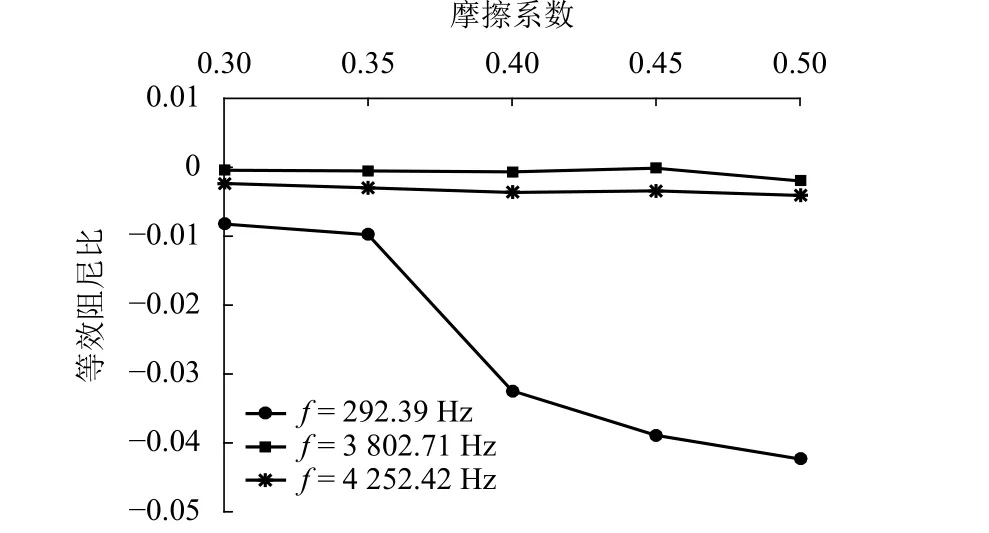
图8 等效阻尼比相对于摩擦系数的变化Fig.8 Variation of effective damping ratio with friciton coefficient

图9 的结果可以定性地解释表1所示的盘型制动系统摩擦噪声发生趋势，表1的数据表明，当F=10.1kN和12.3kN时，盘型制动系统很容易产生摩擦噪声.E2=1.5GPa 时，制动缸推力 F=10.1kN 和 12.3kN时与闸片弹性模量不匹配，制动时容易产生摩擦噪声.

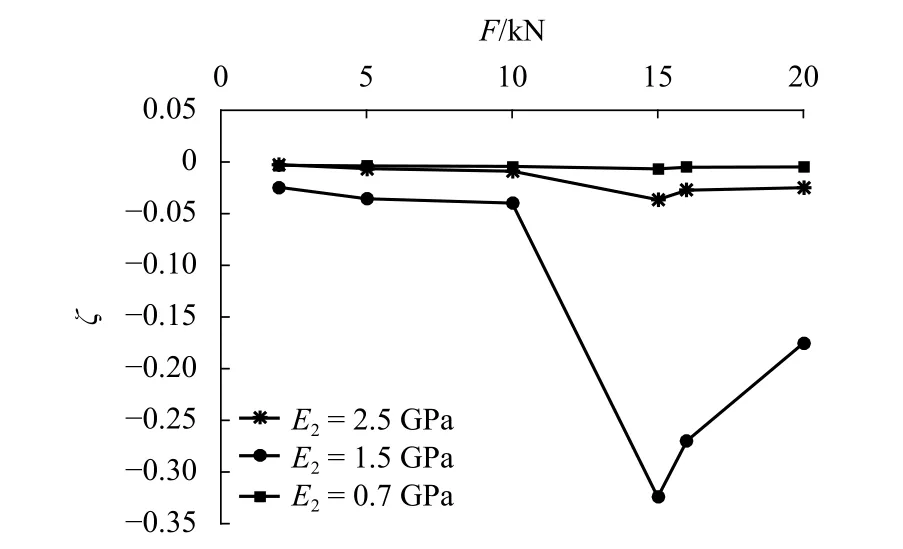
图9 闸片弹性模量对摩擦噪声的影响Fig.9 Effect of the pad modulus on friciton squeal

4 结 论

本文针对某型车辆盘型制动出现摩擦噪声的情况，现场测量了摩擦噪声的实际数据，建立了全尺寸的盘型制动系统自激振动模型，利用复特征值分析法研究了摩擦噪声的发生机理，得到以下结论：

1）实测盘型制动摩擦噪声的主频率为256.78、3904.07、4320.38Hz，盘型制动摩擦噪声的发生与制动缸的推力数值有很大关系，当制动缸的推力F=10.1kN，12.3kN时，盘型制动系统很容易产生摩擦噪声.

2）闸片的弹性模量对盘型制动噪声的发生趋势有很大的影响，当闸片的弹性模量和制动缸推力数值不匹配的时候，盘型制动系统很容易出现摩擦噪声.选取合适的闸片的弹性模量对抑制盘形制动摩擦噪声有利.

3）摩擦系数越大，盘型制动系统就越容易产生制动摩擦噪声.