热压自然通风室内污染物浓度演变特性

庄加玮 ，刁永发 ，张俪安 ，沈恒根

（东华大学环境科学与工程学院，上海 201620）

与机械通风相比，自然通风在降低能耗、提高室内空气质量等方面优势明显，因而自然通风的研究越来越引起人们的重视[1]. 热压自然通风与风压自然通风不同，其往往需经历一段时间的发展才可到达稳定. 对间歇使用建筑而言，热压自然通风向稳态发展的过程相对建筑整个使用阶段的时长并不简短，甚至会占建筑使用的全过程[2]. 因此，依据通风过程气流流动特征，结合室内污染物的初始水平和输送模型，分析热压自然通风室内气态污染物的演变规律具有重要的实际应用价值.

Linden等[3]研究了上下两个通风口的大空间热压自然通风，得到了局部点热源和单一线热源驱动下室内稳态热分层高度以及通风量的理论表达式.Hunt等[4]建立了一种瞬态模型，预测热压自然通风房间热分层到达稳态后污染物浓度随时间的演变，研究表明污染物的衰减率与建筑的几何参数、室内热源的强度、形状以及数量有关. Kaye等[5]假设上层的羽流始终保持均匀混合，建立了一种基于“emptying-water-filling box”的瞬态模型，用以模拟室内外初始温度相同的热压自然通风过程. Yang等[6]对其进行了修正，提出预测瞬时热压自然通风的三层模型，修正后的模型对热分层演化过程的预测精度明显提高. Zhuang等[7]通过引入浮力组合系数，建立了两类非均匀三层模型，与实验数据对比发现非均匀三层模型更具一般性，文献[5-6]的模型仅是其两个特例. 以往研究主要关注稳态或瞬态热压自然通风的热分层和通风率，而对室内污染物演变的报道提及较少，尤其是稳态前的瞬态通风过程. 杨秀峰等[8]虽建立了瞬态污染物冲刷模型，却误将垂直速度为0的分层界面等同于新鲜冷空气层界面，因而，其研究结果也值得商榷.

为此，本文在课题组建立的瞬时热压自然通风非均匀三层模型基础上，依据通风过程室内下层污染物混合特性的不同假设，给出两种浮力驱动自然通风室内气态污染物输送模型，分析两种预测模型下室内污染物层高与浓度的变化规律，并讨论不同无量纲通风面积、浮力组合系数对室内瞬态污染物浓度的影响，从而为瞬时热压自然通风室内污染物浓度预测与控制提供理论支撑.

1 热压自然通风热分层发展模型

热压自然通风初始阶段羽流卷吸进入浮力层的体积通量要大于经上开口流出的体积通量，这使得浮力层厚度变厚，热分层界面向热源方向移动[5]. 经过一段时间发展后，接近稳态流动，其体积通量达到平衡，热分层界面水平保持恒定. 热分层界面处的高度变化率由热羽流从热分层界面卷吸进上层体积流量与浮力诱导从热分层上层带出体积流量的差异决定.

经伯努利方程推导得出通风过程任意时刻通过出风口流出室内的体积流量为[3]

依据热羽流模型[9]，任意时刻点热源驱动自然通风在h处的体积流量为

式中：α 为羽流卷吸系数[10]，α = 0.083； c为常数；B为热源浮力通量.

热羽流到达天花板后会向四周散开并同中间层部分热空气混合形成近天花板层（near-ceiling layer）.因此，近天花板层的热浮力可看成由天花板处羽流热浮力和中间层热空气浮力G的线性组合，也被称为非均匀三层模型[6]. 因通风过程天花板处羽流与中间层羽流的混合度是未知的，可能与通风流动率大小有关[11]，所以浮力组合系数λ取值为0～1用以描述不同层度羽流混合情形. 非均匀三层模型的热分层瞬时演化过程见图1. 图中：箭头表示气体流动方向；T为中间层空气温度；Ta为下层空气温度；Tc为天花板层空气温度；qin为进风口体积流量；为近天花板非均匀层高度[12].

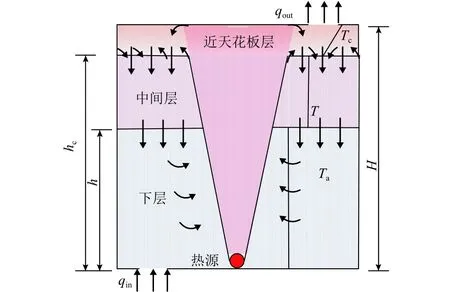
图1 热压自然通风瞬时流动示意Fig. 1 Schematic of transient flow in buoyancy-driven natural ventilation

本文采用精确度更高的热分层预测模型[7]，认为离开房间的羽流热浮力等于，因此，通风过程的瞬时体积流量为

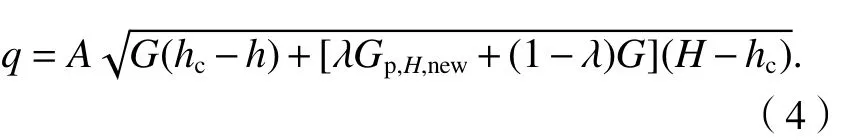
可得室内各热分层体积守恒方程为

式中：S为房间地板面积.

热浮力守恒方程如式（6）所示.

为统一计算，将式（5）、（6）进行无量纲化，分别定义无量纲时间、无量纲高度（为下层无量纲热分层高度，为下层稳态时刻无量纲热分层高度，为近天花板层无量纲热分层高度）、羽流的无量纲热浮力（为中间层无量纲热浮力，为天花板处无量纲热浮力，为近天花板层无量纲热浮力，为出口处无量纲热浮力），如式（8）～（14）所示.

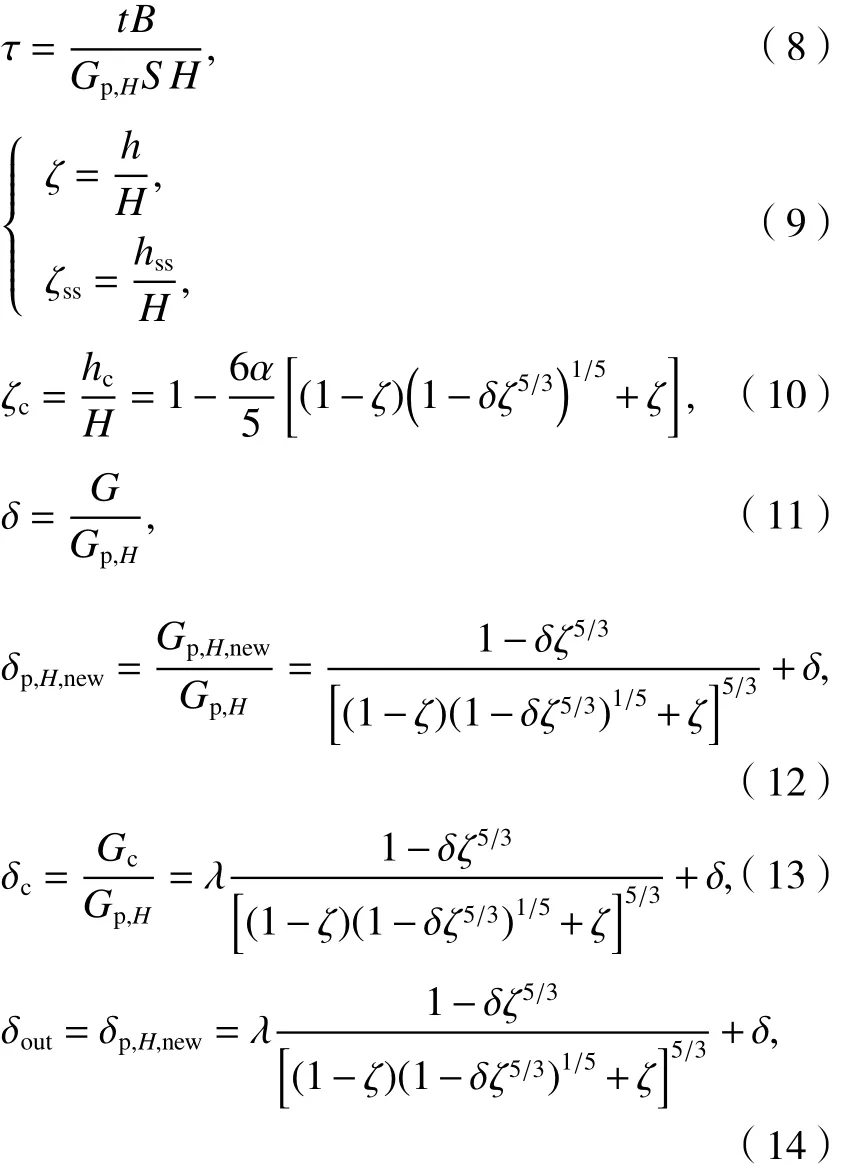
式中：hss为稳态时刻的热分层高度；Gp,H为羽流穿越单一热分层到达天花板处的热浮力[7].

可得无量纲化后的体积守恒方程为

式中：a为无量纲有效通风面积，如式（16）所示.

热浮力守恒方程为

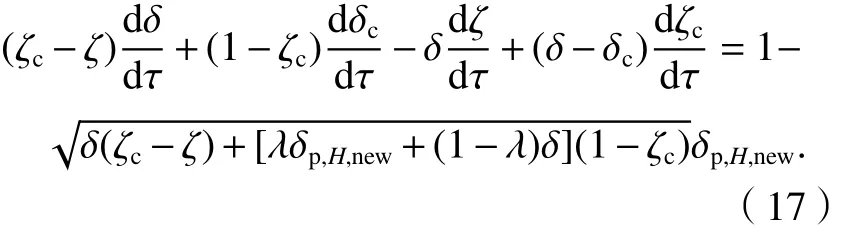
2 热压自然通风气态污染物演变模型

一般情况下房间面积S要远大于任意高度羽流占用的面积b，此时羽流对周围空气的卷吸作用可看作是水平的[9]. 据体积守恒，羽流外任意高度z处空气沿着垂直方向的平均速度为[13]

以往研究多集中在稳定通风条件下的污染物浓度，而不是羽流发展过程中的污染物冲刷过程[4,12]. 本文基于如下两种假设建立起两类预测室内污染物冲刷的瞬时模型[13]：其一，进入室内的新鲜空气与原始的下层空气完全分离；其二，新鲜空气与室内下层空气均匀混合. 此外，假设通风过程中室内上部区域（包括非均匀层和中间层）污染物始终均匀混合. 由于羽流从热源处上升至天花板所用时间短暂，可忽略[14]，故将羽流到达顶部的时刻作为污染物演化的初始时刻.

2.1 纯置换模型（模型Ⅰ）

当流入室内的新鲜冷空气与房间下层原有空气完全分离，图2给出了浮力驱动自然通风污染物演化过程典型分界面气流垂直速度随时间变化的动态过程. 图中：和为通风发展过程两个时间节点；为垂直方向速度为0的界面高度；为新鲜空气层高度；为下层热空气最低高度；为羽流在高度ha处的体积流量.

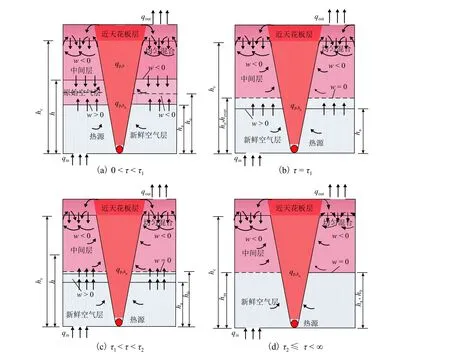
图2 模型Ⅰ下通风过程典型界面垂直速度Fig. 2 Vertical velocities of typical section during ventilation progress for model Ⅰ

纯置换模型（模型Ⅰ）各浮力层（包括上层、原始冷空气层和新鲜空气层）的污染物质量浓度控制方程表示为式（19）～（21）.

上层区域：

将式（24）代入式（19）～（21），得到无量纲表达形式为

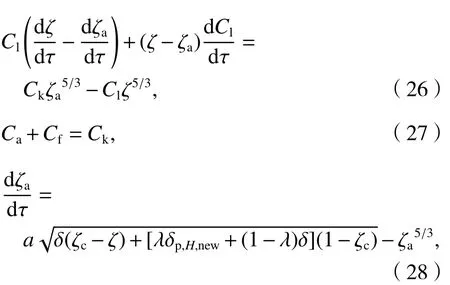
式中：Ca、Cf、Cs和 ζa分别为室外空气、室面污染源、点污染源的无量纲污染物浓度和新鲜空气层的无量纲高度.

气流垂直方向平均速度为0的界面无量纲高度为

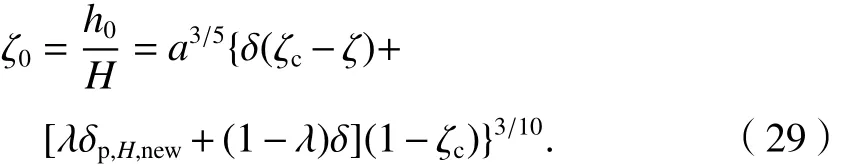
2.2 均匀混合模型（模型Ⅱ）

实际通风过程中，流入室内的新鲜冷空气与房间下层原有空气往往是要进行混合的，这里假设其均匀混合，典型分界面气流垂直速度随时间变化的动态过程如图3所示. 可以看出，模型Ⅱ初期只有2个污染区域，即上部区域（近天花板层与中间空气层）以及下部区域（原有冷空气与新鲜空气混合层），其通风过程污染物浓度分别定义为及.

2.3 模型验证

本文采用4阶龙格-库塔（Runge-Kutta）方法，利用MATLAB 对式（15）、（17）、（25）～（28）、（31）进行求解.

污染物演化模型是在热分层模型的基础上建立起来的. 在前期的工作中已将数值求解结果与前人的理论预测值[5]、CFD （computational fluid mechanics）模拟结果[15-16]、实验数据[5]进行了对比，证明了本文热分层模型的准确性[7]. 故可说明本文所建立的污染物演化模型是可靠的.

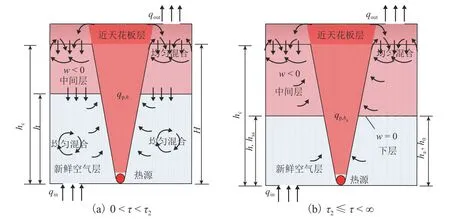
图3 模型Ⅱ下通风过程典型界面垂直速度Fig. 3 Vertical velocities of typical section during ventilation progress for model Ⅱ

3 室内污染物浓度演化分析

由式（25）～（28）、（31）可知，室内不同高度污染物浓度的预测是建立在已有热分层模型的基础上.因此，两种污染物预测模型在任何形况下都有相同的ζ.

图4给出了热压自然通风过程中，污染物层高的瞬时变化.

图4 污染物层高的瞬时变化Fig. 4 Transient change of pollutant height

如图 4（a）所示，当 a = 0.2，λ = 0.5 时，通风开始后，ζ迅速从房间顶部向下移动，而ζ0和ζa都从地板面向上移动. ζ0一直大于ζa，直至通风到达稳定τ2=8时，两者重合. 另一方面，因ζ0具有更大的变化率，其与ζ在更早的时刻τ1已经重合，此时两者的高度都等于热分层最低高度ζover. 由于热惯性力的作用[17]，ζ0要稍大于ζ，后缓慢减低并在稳定时刻τ2两者完全重合，此时3个热分界面的高度都为ζss，这表明最终室内污染物分层仅存在上层和新鲜空气层.ζ0和ζa不具备相同的变化趋势，污染物演化过程中是两个不同的分界面，这与文献[13]中的假想一致.通风开始后，室内原始冷空气层厚度ζ-ζa变得越来越薄，ζ0将室内原始冷空气层分割成两个小的污染层，其厚度分别为 ζ-ζ0和 ζ0-ζa. 由 ζ-ζ0和 ζ0-ζa的变化曲线可以看出，ζ-ζ0随着时间不断变小，而 ζ0-ζa则先迅速增大，后开始逐渐变小. 在到达τ1=3时，ζ-ζ0消失，此时 ζ-ζa和 ζ0-ζa两条污染物浓度变化曲线重合，这意味着 ζ0-ζa= ζover-ζa.

图4（b）给出了不同 a 下 λ对 ζ0-ζa变化趋势的影响. 可清楚地看出，无论a的取值，ζ0-ζa都有相同的变化趋势，即先迅速增大后缓慢减小，且a值越大，ζ0-ζa的峰值越大，到达稳态消失的时间反而越短. 此外，由图4（b）还可以发现，在初期阶段λ越大，ζ0-ζa越大，而后则反之，并且这种影响随着a值的增大越发明显.

为了说明两种预测模型下，室内不同热分层内污染物的演化过程. Cs= 0.1，Cf= 0.1，Ca= 0.1，a = 0.2，λ = 0.5时通风过程室内污染物浓度的变化如图5所示.

图5 a = 0.2，λ = 0.5时污染物浓度的瞬时变化Fig. 5 Transient change of pollutant concentration for a = 0.2 and λ = 0.5

由图5（a）可以看出，模型Ⅰ的室内污染物可分为3层. 其中，Cu和Cl有相近的变化规律，即污染物都随时间的推移不断被新鲜空气冲刷带出，浓度一直降低至恒定值. 而Ck始终保持恒定不变，大小等于点污染源和面污染源两种污染源强度之和，即Ca+Cf. 室内原有污染层要早于室内上层达到污染物浓度稳定值，其最终大小与新鲜空气层相同. 在τ1= 3时，ζ-ζ0消失，此时的 Cl就是污染层 ζ0-ζa的浓度.当室内热分层到达稳定时刻τ2= 8时，上层污染物浓度要稍高于稳态值Ca+Cf+Cs，并随时间推移到达稳定.

值得注意的是，Cu在初始阶段的短暂时刻会急剧增大，后在此基础上缓慢衰减. 这是因为，对于室内热空气上层而言，通风过程中该层受到来自室内原始污染层和点污染源释放的污染物污染，且在初始时刻进入该层的羽流量要远远大于离开的羽流量，但初始时刻Cu和Cl保持一致，从而使得该层的污染物总量迅速增加，另一方面，在初始时刻室内污染物上层厚度1-ζ无限接近于0，因此造成了该层污染物浓度地显著增大；在此之后，因流出羽流所携带污染物的总量要大于流进的量，上层的污染物浓度又随之下降.

图5（b）给出了 a = 0.2，λ = 0.5 条件下两种模型预测结果的对比，相较于模型Ⅰ，模型Ⅱ在通风过程中污染物仅分为上下两层. 可以发现，两种预测模型的上两层污染物都有相似的变化趋势，且上层的污染物浓度最大，不同的是，模型Ⅰ在初始时刻的变化比较平缓，后会急剧下降；而模型Ⅱ则会一直缓慢衰减. 另外，到达稳定状态后，Cl和、Cu和的大小分别相同，这也说明下层污染物混合特性会影响室内污染物分层以及浓度演变特性，但不会改变稳定时刻室污染物浓度分布.

对于两种污染物预测模型，图6给出了Cs= 0.1，Cf= 0.1，Ca= 0.1时，a和λ对污染层浓度瞬时变化的影响. 结果表明，a对不同污染层有相同的影响，即a值越大，污染物浓度衰减越快，到达稳定时刻的时间越短；反之越慢，到达稳定用时越长. 特定的a值，任意时刻由于λ引起的污染物浓度差异是微乎其微的，即使这种差异会随着a的减小而有所增大，但总体上可以得出λ对不同污染层浓度变化的影响几乎可以忽略.

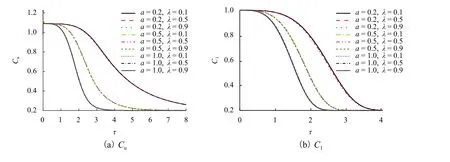
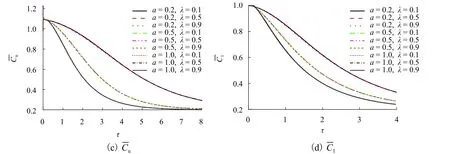
图6 a 和 λ 对污染物浓度瞬时变化的影响Fig. 6 Effects of a and λ on transient variation of pollutant concentration

4 结 论

为实现对热压自然通风瞬时过程室内气态污染物的快速预测，在热分层瞬时变化非均匀三层模型基础上，结合室内不同的下层污染物混合特性，构建了两种热压自然通风室内污染物输送模型，分析了通风过程室内污染物层高与浓度演变特性，并考察了有效通风面积和λ对污染物浓度变化的影响. 得到如下主要结论：

1） 通风过程 ζ0和 ζa是两个不同的分界面. ζ0将原始污染层分割成两个区域，其厚度分别为ζ-ζ0和ζ0-ζa，ζ-ζ0会随着时间不断变小，而 ζ0-ζa则先迅速增大，后开始逐渐变小. ζ随时间逐渐变薄，而ζa则逐渐增大，到达稳定后 ζ、ζ0、ζa3 个界面重合，均等于ζss.

2） a 越大，ζ0-ζa可到达的峰值越大，衰减过程所需的无量纲时间反而越短； λ 值越大，任意时刻对应的 ζ0-ζa越大，且这种差异随着 a的增大越发明显.

3） 对纯置换模型，Ck恒等于 Ca+ Cf，Cl随时间不断衰减，稳定时浓度为Ca+ Cf，而Cu在初始阶段急剧升高，后在此基础上缓慢降低，其稳定值等于Ca+ Cf+ Cs；对于均匀混合模型，、

变化会更平缓一些，稳定值分别为Ca+ Cf、Ca+ Cf+ Cs. 说明下层污染物混合特性会影响室内污染物分层以及浓度变化特性，但不改变稳定时刻室内污染物浓度分布.

4） 通风过程任意时刻上层污染物浓度都要大于下层，a值越大，各污染层无量纲污染物浓度下降越快，排污效率越高；而λ对污染层浓度变化的影响则很小.