混凝土空心墩塑性铰区抗剪计算模型比较分析

2021-02-01邵长江漆启明胡晨旭

西南交通大学学报 2021年1期

邵长江，漆启明，韦旺，胡晨旭

（1. 西南交通大学土木工程学院，四川成都 610031；2. 西南交通大学陆地交通地质灾害防治技术国家工程实验室，四川成都 610031）

高墩大跨桥梁是西部山区的优选桥型，为了减小恒载、降低墩身基础经济投入和优化动力性能，高墩往往采用空心截面[1]. 然而，西部山区往往强震频发，为确保该区域高墩桥梁的抗震安全性，一般需要遵循能力保护原则（“强剪弱弯”）进行抗震设计，确保空心墩具有足够的抗剪能力，并在强震下发生期望的延性破坏. 由于混凝土构件抗剪机理的复杂性，目前混凝土墩抗剪性能的研究还比较薄弱；同时现行抗震规范仅适用于中低墩规则梁桥，尚未明确给出切实可行的空心高墩抗震设计方法[2]. 加之2008年汶川震害中，百花大桥、回澜桥等均因部分实心桥墩潜在塑性铰区配箍率较低发生了剪切或弯剪破坏[3-4]，而相对于上述发生震害的实心墩，空心墩由于约束混凝土效应的削弱，在很大程度上影响到桥墩的抗剪性能[5]，因此针对强震区空心墩塑性铰区抗剪性能的研究很有必要.

钢筋混凝土墩柱的抗剪能力受多种因素影响，现有计算公式大多为半理论半经验的形式. 一般认为混凝土构件的抗剪能力主要由箍筋和混凝土两部分组成[6]，人们关于箍筋的抗剪贡献认识比较统一，对混凝土抗剪能力影响因素（除混凝土强度外）的描述不胜枚举[7]. Priestley等[8-9]认为在一定范围内延性对抗剪能力有较大影响，在此基础上Kowalsky等[10-12]还引入了剪跨比及纵向配筋率的影响，文献[8-12]中的公式的共同特点是将轴力对抗剪的贡献单独作为叠加项进行考虑. 但更多的模型将轴力贡献计入于混凝土抗剪部分：Aschheim等[13]在轴力的基础上考虑了延性的影响；Caltrans[14]和《城市桥梁抗震设计规范》（以下简称《城规》）[15]同时考虑了延性、箍筋和轴力对混凝土分项的影响；ACI-318[16]在公式中仅考虑了轴力变化，直接给出较为保守的强度退化系数（定值）；顾毅云[17]考虑因素与Aschheim相同，但公式中用轴压比η代替轴力P；Sezen等[18]则给出包含延性、剪跨比和轴力因素的混凝土分项公式，Shin等[19]在Sezen的基础上考虑了纵筋率的影响；NZS 3101[20]认为除轴力外，纵向受拉钢筋的配筋率也对混凝土抗剪贡献有影响. 除此之外，有少数模型并没有考虑轴力变化对混凝土分项的影响：JRA—2002[21]认为混凝土部分抗剪能力与荷载类型、几何尺寸和纵向受拉钢筋有关；《公路桥梁抗震设计细则》（以下简称《细则》）[22]中的抗剪能力只与自身混凝土强度有关.

上述抗剪计算模型形式多样、考虑因素不一，且涵盖抗剪承载力评估公式[8-11,13,17-19]和规范中的抗剪设计公式[12,14-16,20-22]，这些公式能否直接用于混凝土空心墩的抗剪计算、计算效果如何，成为本文的研究焦点. 因此，作者通过引用文献中25个剪切或者弯剪破坏的空心墩拟静力试验结果[11,23-27]，分析空心墩塑性铰区抗剪能力的影响因素，并利用国内外现行规范及相关学者给出的公式进行抗剪评估，对比分析各公式关于空心墩抗剪计算的适用性，并给出塑性铰区抗剪分析的建议公式.

1 空心墩抗剪机理及研究

1.1 空心墩塑性铰区抗剪机理

钢筋混凝土墩柱在强震作用下塑性铰区需要同时承受轴力N 、剪力V和弯矩M的共同作用. 出现斜裂缝后，空心墩潜在塑性铰区斜截面的抗力[9]如图1（a）所示：1）截面受压区高度c内的轴力P抗剪贡献Vp和混凝土抗剪贡献 Vc；2）箍筋抗剪贡献Vs（Avfyv），Av为箍筋面积，fyv为箍筋屈服强度；3）纵筋承受拉力Ts的同时，会对混凝土产生销栓力Vj；4）斜裂缝间的摩擦力 Vf及骨料咬合力 Vk；5）地震力F. 随着塑性铰区塑性变形所生产弯剪裂缝宽度的增加，降低了骨料咬合传递的剪力，由此会导致桥墩抗剪能力的迅速下降[8,28]. 因此在混凝土抗剪能力计算时，通常仅考虑轴力、混凝土和箍筋的抗剪贡献. 试件POI-N6东面E内侧在不同Dr时的破坏特点如图1（b）所示[27]，Dr为墩顶位移与墩高之比.

图1 桥墩塑性铰区开裂后局部受力及破坏特点Fig. 1 Local mechanical and damage behaviors in plastic hinge after cracking of concrete pier

在延性抗震设计中，为了避免出现脆性破坏，相关学者基于实心墩在探究剪切破坏机理的基础上给出了抗剪能力计算公式，即基于古典桁架模型计算箍筋的抗剪贡献[6]，根据试验结果回归混凝土的抗剪能力[8-10,13,17-18]，进而给出半理论半经验的抗剪公式，现行规范中的抗剪模型[12,14-16,20-22]也属于此类，且多数源于实心墩的试验成果.

1.2 空心墩抗剪性能研究

同实心墩相比，空心墩的约束混凝土效应大大减小[1]，在抗剪机理上存在较大差异[5]，故部分学者针对空心墩进行了抗剪性能研究[11,23-27]. 表1列出了弯剪或剪切破坏空心墩的试件（编号为S1～S25）参数[11]，表中：L为计算墩高；h为截面高度；为空心墩的壁厚；为混凝土轴心抗压强度；为纵筋屈服强度；为纵向配筋率；为加载方向箍筋的屈服强度；为加载方向配箍率；s为箍筋间距；μmax为最大承载力对应位移延性；μΔ为弯剪破坏试件承载力下降至最大承载力80%对应的位移延性；Vmax为最大侧向力；VM为截面弯曲破坏时对应剪力设计值. 各墩最终破坏模式遵从原文献，并利用Xtract计算了各墩截面弯曲破坏时对应剪力需求VM. 空心墩破坏现象同实心墩的差异显著（如图1（b）所示），除在侧面形成明显剪切裂缝外，由于扣除内部核心混凝土，空心墩内壁也会同样出现明显剪切裂缝和混凝土剥落，进而导致空心墩抗剪能力削弱，在强震下更易发生剪切破坏. 各试件剪力需求VM和最大侧向力Vmax接近，与弯剪破坏的试验现象一致[28]. 对于剪切破坏试件，通常取最大侧向力Vmax作为其抗剪强度试验值Vtest，而关于弯剪破坏桥墩的抗剪强度值则存在较大争议. 已有研究表明桥墩抗剪强度在一定范围内会随延性系数μ的增加而降低，如文献[8-11, 18-19]认为抗剪强度在μ= 2开始降低，当μ增大到一定程度时混凝土残余抗剪强度不变. 因此，本文取侧向力降低至0.8Vmax作为弯剪试件的破坏点[11,18]：若μ≤ 2，则取最大承载力Vmax作为空心墩抗剪试验值；若μ＞ 2，则取0.8Vmax作为抗剪试验值.

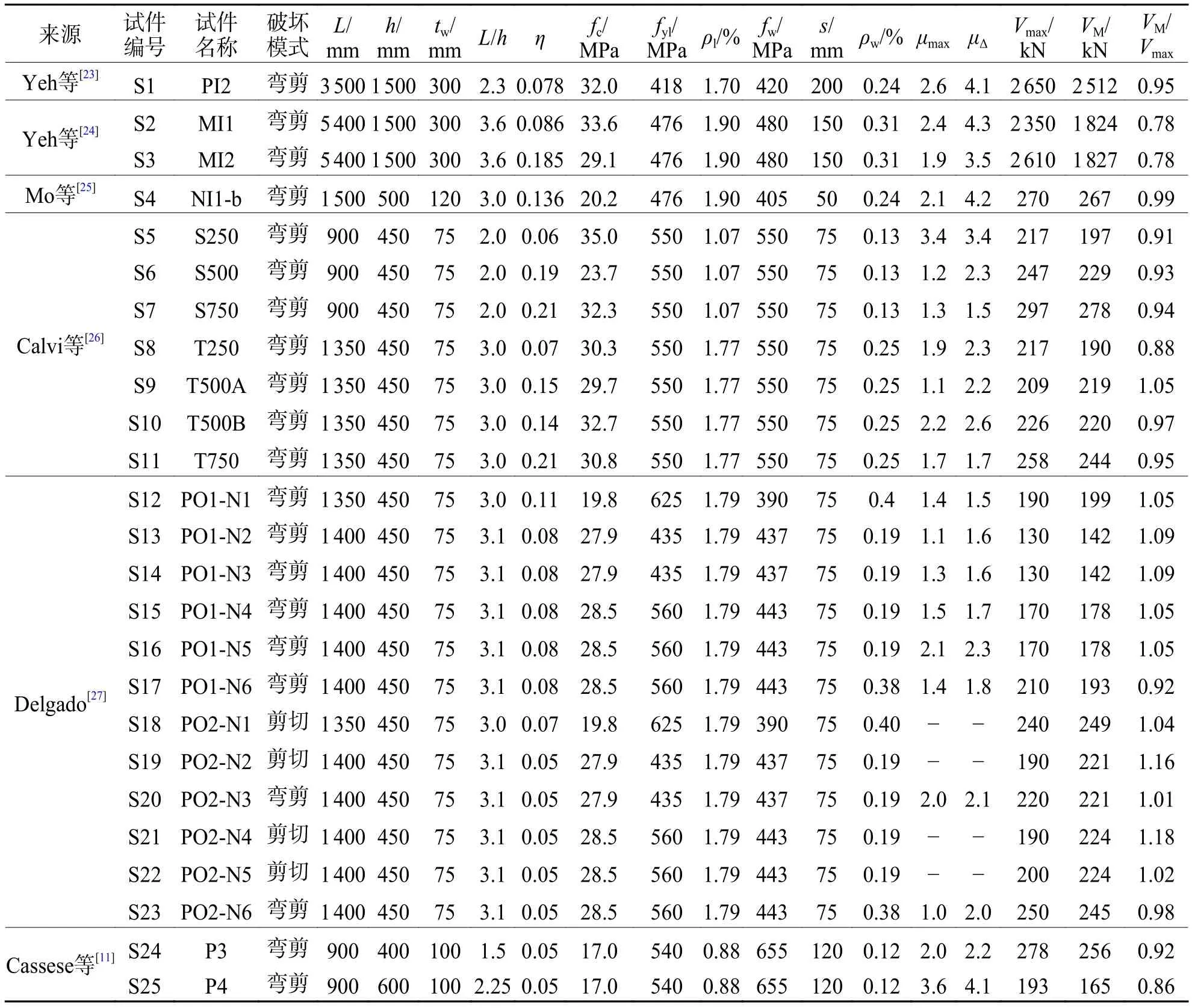
表1 空心墩的设计参数Tab. 1 Design parameters of hollow piers

2 抗剪能力计算公式

影响墩柱抗剪能力的因素众多，由此得到的抗剪公式复杂多样，为便于梳理分析，作者根据轴力的考虑方式将公式分类如下.

2.1 轴力贡献单独考虑

Priestley等[8]认为桥墩的抗剪承载力Vn包括Vc、箍筋贡献Vs和轴力贡献Vp3部分. Xiao等[9]的试验表明，混凝土抗剪能力随着延性系数μ的增加会大幅度的减小，修正了μ较大时Priestley公式的混凝土分项退化系数γ. Kowalsky等[10]在Priestley公式的基础上，考虑了剪跨比和纵向配筋率对混凝土抗剪的影响，同时修正了退化系数. Cassese等[11]根据弯剪破坏的空心墩拟静力试验结果，建议将Kowalsky公式中的混凝土有效剪切面积由0.8Ag（Ag为截面的毛截面积）替换为腹板的有效面积1.6twh.与Kowalsky类似，Eurocode8[12]的抗剪公式也考虑了延性、剪跨比和纵筋率对混凝土部分抗剪的影响，但其认为箍筋抗剪分项随着延性的增加也会出现降低，故采用了与混凝土一样的强度退化系数. 表2所示公式的共同特点是将轴力对墩柱抗剪的贡献（“拱效应”[8]）作为单独项Vp考虑，且其计算公式均相同；而箍筋抗剪Vs中的有效高度取值及裂缝与轴线的角度θ则略有差异. 表2中：抗剪贡献Vp均为（h-c）P/（2L）；α为剪跨比修正系数（修正系数在各公式中具体取值不一样）；β为纵向配筋率的修正系数；ccov为混凝土保护层厚度；计算时θ= 30°；bw为截面腹板厚度.

表2 轴力考虑为单独项Vp的抗剪模型Tab. 2 Shear strength models considering axial-load in Vp

2.2 轴力贡献计入混凝土分项

上述轴力考虑方式概念清晰，计算简洁. 但更多的成果（如表3所示）将轴力计入混凝土分项考虑[13-20]，认为轴力在一定范围内提高了受压区混凝土承担剪力和咬合力，进而增强墩柱抗剪能力[17]. 表3各模型中：M11的箍筋抗剪贡献为γAvfyvd/s，其余模型的箍筋抗剪贡献均为Avfyvd/s；pw为截面受拉纵筋的配筋率；为混凝土抗剪能力随延性系数μ和ρsfyv的修正系数，ρs为体积配箍率.

表3 轴力贡献计入混凝土分项Vc的抗剪模型Tab. 3 Shear strength models with the effect of load P in Vc

Aschheim等[13-17]考虑轴力变化的方式接近，均直接将轴力的贡献转化为公式中一个修正系数. 其中，Aschheim等[13]还考虑了延性对于混凝土抗剪的影响，随后该模型被FEMA273[29]采纳；Caltrans[14]和《城规》[15]还考虑了延性及箍筋对混凝土分项的影响，且两者公式形式相同，仅在修正系数的取值上略有差异；而ACI-318[16]公式中仅考虑了轴力因素，并且直接给出一较保守的强度退化系数（定值）以考虑延性增大对于混凝土抗剪能力的削弱；顾毅云[17]在公式回归时选用轴压比和延性系数作为主要影响因素，而轴压比本质上仍是轴力的体现.

Sezen等[18]则将轴力转化为单元应力，基于材料力学理论推导了混凝土剪切应力的表达式. Shin等[19]结合13个无箍筋的混凝土空心墩，在Sezen的基础上增加了纵向配筋率的影响，进一步修正了混凝土的抗剪贡献. NZS 3101[20]认为当轴压比低于0.1时，可忽略塑性铰区混凝土的抗剪，反之则考虑混凝土的抗剪作用，并且认为受拉钢筋配筋率对抗剪能力也有一定的影响.

2.3 不考虑轴力变化的影响

部分成果（如表4所示）未考虑轴力变化对混凝土抗剪分项的影响[21-22]. 表4中：vc为混凝土能够承担的平均剪切应力度；kc为关于载荷的正负交替反复作用的影响的修正系数；ke为d的修正系数；kpt为有关轴方向拉伸钢筋比的修正系数；为截面的有效宽度. 需要注意的是，JRA规范中箍筋抗剪能力贡献的有效高度与箍筋角度有关，本文试件箍筋与主轴角度均为90°，故直接为d.

表4 不考虑轴力变化影响的抗剪模型Tab. 4 Shear strength models without the effect of varying P

JRA[21]抗剪强度模型未采用能力设计方法，公式考虑了尺寸效应和纵向配筋率的影响，并引入反复荷载效应系数以考虑混凝土抗剪强度降低的影响. 而《细则》[22]中桥墩抗剪部分没有区分塑性铰与非塑性铰区，抗剪能力直接采用Caltrans塑性铰区抗剪强度的下限值，即只与混凝土强度有关.

以上模型中抗剪强度的指标含义有所不同，大部分可评估不同延性桥墩塑性铰区的抗剪能力；部分规范公式（ACI-318、NZS 3101、JRA和《细则》）未考虑延性影响，偏保守地用于墩柱抗剪设计，本文着重探讨既有评估公式的适用性.

3 比较分析

3.1 影响因素比较

上述公式考虑因素及所采用参数汇总于表5.表中： Caltrans和《城规》中延性范围随轴压变化，顾毅云公式未给出延性变化范围；若箍筋抗剪公式中未明确为30°，均取45° 进行计算.

表5 各抗剪模型影响参数Tab. 5 Influencing factors in each shear strength model

影响桥墩抗剪能力的因素包括混凝土强度、配箍率（和箍筋强度）、延性系数、轴力（轴压比）、剪跨比和纵向配筋率等[5]. 结合表1中空心墩试验数据，给出名义抗剪强度随影响因素的变化趋势[18]，如图2所示，图中，Vtest为抗剪强度试验值.

分析表5和图2可知，混凝土强度和箍筋贡献在各公式中均有体现，除JRA和《细则》外其余公式均考虑了轴力变化对抗剪强度计算的影响，大多数模型（除ZNS 3101、JRA和《细则》）还将位移延性系数引入公式中. 由此，可以认为混凝土强度、箍筋、轴力和位移延性是影响墩柱抗剪能力的核心因素，结合这些因素在各公式中体现形式和图2可得桥墩抗剪强度随混凝土强度、配箍率（或ρwfyv）和轴力（或轴压比）的增加而提高，一定范围内随位移延性的增加而降低. 部分公式（Kowalsky、Cassese、Eurocode 8、Sezen和Shin）考虑了剪跨比变化的影响，认为剪跨比仅在一定范围内对桥墩抗剪强度产生影响，而图2结果说明纵筋率影响不显著. 为便于进一步比较各模型，在此规定：1） μ为极限位移与首次屈服位移的比值；2） d为核心混凝土受压边缘至受拉侧钢筋重心的距离[15,18]；受压区 c/h取值为 0.25～0.35[10]，在此取0.3；其余各系数可参照设计参数确定.

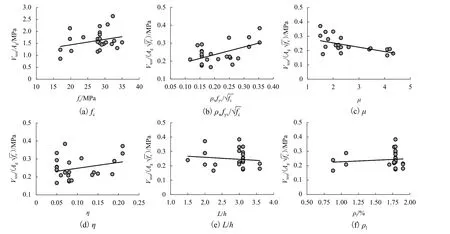
图2 名义抗剪能力随不同试验参数的变化Fig. 2 Variation of normalized shear strength with different test parameters

3.2 各公式比较

在桥墩基本参数确定后，位移延性成为影响其抗剪强度的重要因素. 为比较不同位移延性系数下各公式的计算结果，作者以表1中试件S25的参数为例，计算延性系数在0～10范围内的抗剪强度，结果如图3所示. 可见，文献中的抗剪计算公式和部分规范设计公式（Eurocode 8、Caltrans和《城规》）均考虑了强度随位移延性增加而降低的特性，剩余规范公式（ACI-318、NZS 3101、JRA和《细则》）则未考虑延性影响，计算结果相对保守，远低于试件S25的破坏强度. Priestley和Sezen模型较好预测了试件S25在破坏时的抗剪强度，但各公式计算结果仍需和更多空心墩试验数据比较，以探讨各评估公式的准确性和各规范设计公式的安全余量.

图3 各抗剪模型随位移延性系数的比较Fig. 3 Comparison of shear models in terms of ductility factor μ

3.3 计算值与试验值比较

利用表2～4中公式计算表1中各试件的抗剪强度，图4为各墩抗剪强度计算值Vcal与试验值Vtest的比值变化情况，表6为各模型比值的均值及变异系数，图5为各模型中不同部分抗剪贡献所占比例均值（图中：Vcal-1为箍筋抗剪贡献计算结果的均值；Vcal-2为箍筋和混凝土抗剪贡献计算相加后的均值）.可知：除NZS 3101、JRA和《细则》外，各模型Vcal/Vtest比值的变化趋势近乎一致，说明这些公式对抗剪机制的认识较为统一，只是变化幅度有所不同.

试件S3、S11、S15和S16的抗剪强度比值普遍偏大，桥墩试验的离散性可能是主因；多数公式中试件S1和S24（剪跨比分别为2.3和1.5）抗剪强度比值趋势偏小，可能原因是剪跨比较小时桥墩的抗剪能力小幅增强；试件S6和S9在不同公式下比值变化趋势不同，可能是因为各公式考虑的影响因素不同. 公式M1～M3中计算角度取30°，比值整体偏高；公式M6～M15的箍筋抗剪贡献比较接近，但混凝土的贡献差异较大，导致各模型计算值差异较大.

Priestley、Xiao、Kowalsky、Cassese、《城规》和顾毅云计算值与试验值的平均值分别为1.52、1.30、1.32、1.09、1.13和1.14，上述模型高估了空心墩的抗剪能力（超过5%），使得空心墩的抗震设计偏于不安全. NZS 3101、JRA和《细则》所得计算值与实测值的平均值分别为0.48、0.50、0.46，低估了桥墩塑性铰区的抗剪能力；Eurocode 8和ACI-318的比值平均值分别为0.75和0.80，计算结果略微保守. Aschheim、Caltrans、Sezen和Shin比值的平均值误差在5%以内，分别为0.99、0.98、1.01和0.97，所得计算结果与试验值较为接近.