圆拱结构平面外稳定分析方法

丁 敏 ，王佳佳 ,2，蒋秀根 ，曹琼琼 ,3，王宏志

（1. 中国农业大学水利与土木工程学院，北京 100083；2. 北京科技大学后勤管理处，北京 100083；3. 铁总服务有限公司房产建筑管理处，北京 100844）

通常将在面内荷载作用下产生相互耦合面内压弯变形的结构称为拱，将在面外荷载作用下产生相互耦合面外弯扭变形的结构称为曲梁，当轴线为圆弧线时，二者分别称为圆拱与圆曲梁. 圆拱结构由于支座水平推力大大降低了截面弯矩而具有较高的刚度和承载力，广泛应用于各类大跨度桥梁结构和温室结构[1-2]中，如琼州大桥以及我国现代农业中大面积使用的拱棚温室.

圆拱结构由于截面轴压力较高，且一般跨度较大，构件具有较大的长细比，当截面刚度不足时非常容易发生稳定失效. 圆拱结构的平面外失稳涉及面内外受力耦合以及面外弯扭变形耦合，同时还涉及复杂的几何非线性问题，具有大变形、大位移特征.圆拱结构的平面外稳定性能常常决定了圆拱结构的安全性能，因此，寻找圆拱结构平面外稳定分析方法，一直是学者关注的焦点.

圆拱结构平面外稳定分析的有效方法通常有3种：静力法、能量法和有限元法. 静力法是基于圆拱结构平面外变形的静力基本方程，结合边界条件，建立圆拱结构在临界状态下的齐次静力方程，从而求得临界荷载，准确区分微分方程特征，获得正确的挠度方程是其重要环节. 铁摩辛柯[3]给出了特定拱的平面外分岔失稳临界荷载；项海帆等[4]得到了自由扭转曲梁偏大的临界荷载值；郭彦林、窦超等[5-11]推导了考虑翘曲扭转的圆曲梁挠度方程的一般格式，但是由于未能准确区分常系数微分方程解的特征，给出了不正确的挠度方程，无法用于圆拱结构平面外稳定分析的解析求解；邓婷[12]建立了圆拱结构平面内静力分析的大位移模型，并给出了分岔失稳分析解析计算方案及各类拱的平面内分岔失稳临界荷载及失稳模态. 能量法[13-23]是选取合理的屈曲模态，建立圆拱结构平面外的能量方程，利用能量原理建立屈曲失稳特征方程. 该方法避免了建立并求解圆拱结构平面外弯扭位移方程，但在求解圆拱结构平面外分岔失稳时，需假设满足边界条件的圆拱结构位移函数，通常存在主观性，不能准确表达圆拱结构平面外弯扭位移的根本特征；求解精度取决于所取模态的合理性，结果一般为近似解，且只能得到偏大的临界荷载. 有限元法不受圆拱结构形式、荷载方式的限制，可以分析圆拱结构分岔失稳和极值点失稳的临界荷载及失稳模态，是学者们分析圆拱结构平面外稳定问题常用的方法[6,24-27]. 但该方法只能采用直梁拟合圆拱，即采用割线拟合弧线，且采用了与圆拱位移差异较大的多项式位移形函数，计算所得的临界荷载值误差较大.

考虑到圆拱结构平面外失稳变形与圆曲梁变形的相关性，本文将针对圆拱结构的平面外稳定问题，首先根据圆曲梁基本受力特点，采用静力法建立考虑大位移的自由扭转圆曲梁基本方程，得到圆曲梁几何非线性静力分析的统一解析模型，在此基础上将其应用于圆拱结构平面外分岔失稳及平面外极值点失稳分析，为圆拱结构的稳定问题提供一种新的分析方法.

1 圆曲梁大位移模型控制方程

1.1 模型参数与基本假定

为方便表达圆曲梁中各物理量，同时选取随动极坐标系和三轴坐标系如图1所示. 其中：随动极坐标系中，圆曲梁轴线半径为r，圆心角为φ，弧长l =rφ；三轴坐标系中按右手螺旋法则定义，O′为其坐标原点；mx、qy、qz和 mz分别为 x方向分布力矩、y方向分布力、z方向分布力和 z方向分布力矩；v、θx、θz、κz、κx分别为 y方向的位移、x方向的转角、弯曲转角、微段绕z轴的弯曲曲率、微段绕x轴的曲率；N0、Mz、Vy和Tx分别为轴力、相应坐标轴方向的截面弯矩、剪力和扭矩，均假设与坐标轴方向一致为正.

定义η = EIz/(GId)为弯扭刚度比，其中，GId为绕x轴的抗扭刚度，EIz为绕z轴的抗弯刚度；λ =N0r2/(EIz)为轴力系数. 假设所研究对象为处于弹性阶段受力的等曲率等截面平面曲梁，忽略截面剪切变形，考虑轴力在挠度上对截面产生的二阶弯矩，且采用线性弯曲曲率模型，基于圣维南自由扭转，不考虑扭转截面翘曲及轴力和弯矩产生的二阶扭矩.

图1 圆曲梁坐标系Fig. 1 Coordinate system of circular curved beam

1.2 静力平衡方程

根据圆曲梁受力变形特点，写出其考虑大位移的内力平衡方程、几何方程和物理方程[1].

1） 平衡方程

弯矩平衡方程：

1.3 静力控制方程

综合圆曲梁基本方程式（1）～（8），可以得到圆曲梁位移控制方程.

1） 挠度控制方程

2） 扭转角控制方程

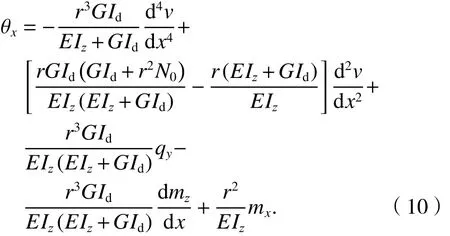
2 圆曲梁位移及内力

2.1 圆曲梁位移

1） 挠度和扭角的一般格式

由挠度控制方程（式（9）），求得圆曲梁挠度为

式中：vh和vp分别为挠度通解和特解.

综合式（10）、（11），可以得到圆曲梁扭角：

式中：θxh和θxp分别为扭角通解和特解.

2） 位移简化格式

定义圆曲梁挠度和扭角表达式分别为v = fvd+vp和 θx= fθd + θxp，其中：fv和 fθ分别为挠度和扭角的基函数向量；d为曲梁位移系数向量. 根据以上分析，圆曲梁压弯受力变形共有6个独立位移变量d1～d6，与圆曲梁自由度总数相同，且仅考虑圆曲梁自由扭转，定义

根据微分方程特征根的特性可以发现，不同轴力下圆曲梁位移呈现不同的方程格式，定义 -1/η ＜λ ＜ 0 时为低轴压力范围，λ ＜ -1/η 时为高轴压力范围. 根据圆拱平面外失稳特性，将不同工况下有轴压力圆曲梁的位移进行细化，对应基函数形式如表1所示.

表1 不同工况下圆曲梁位移简化表达式Tab. 1 Simplified expressions for displacement of circular curved beam under different load conditions

显然：

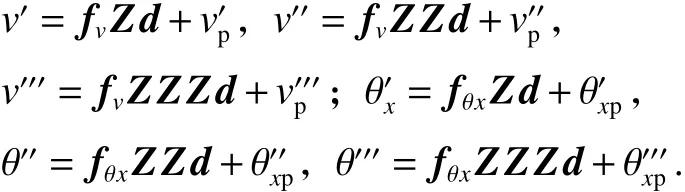
2.2 圆曲梁变形

根据圆曲梁几何方程式（4）～（6），结合圆曲梁位移、导数转换矩阵，求得圆曲梁的弯曲转角、弯曲曲率及扭率分别为

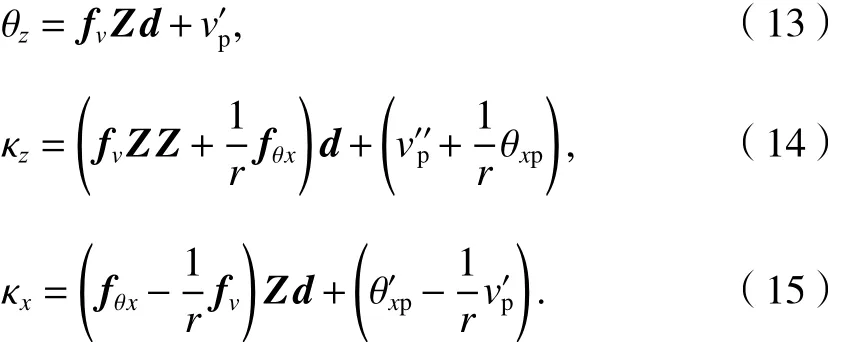
2.3 圆曲梁内力

根据圆曲梁物理方程式（7）～（8），结合圆曲梁变形，可求得圆曲梁的弯矩及扭矩分别为

结合式（1）、式（16）～（17）及圆曲梁挠度方程，可得圆曲梁剪力的矩阵表达式为

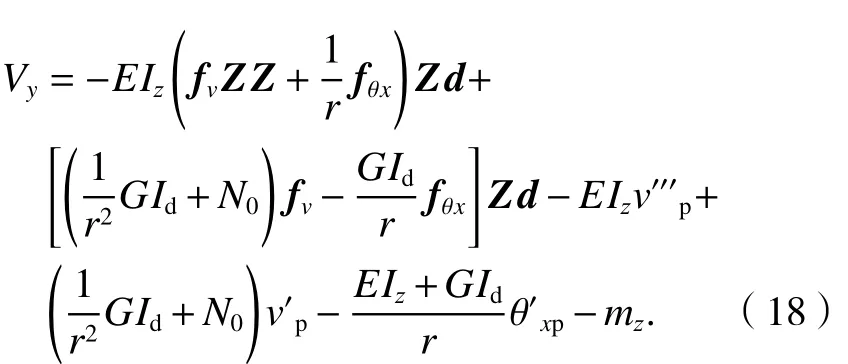
3 圆拱结构平面外分岔失稳分析

3.1 分析方法

结合圆拱结构平面外边界条件，根据圆拱结构平面外位移方程对圆拱结构平面外失稳进行分析.其中，圆拱结构平面外位移方程可根据圆曲梁位移方程确定；圆拱结构平面外边界条件可根据圆曲梁边界条件确定，详见表2，表中：B为双力矩.

具体分析步骤如下：

1） 边界位移方程

对圆拱结构进行分岔失稳分析时，圆拱上只有产生无矩拱条件的面内荷载，圆拱面外荷载必然为0. 利用圆拱平面外边界条件建立的方程为位移系数定解方程，该方程一定是齐次方程. 故定解方程组数和位移系数总数相同. 根据此方程可得到有位移时圆拱内力参数和对应的位移系数的相对关系（即位移模态）. 该齐次方程用向量形式表示为

式中：A(λ，θ)为位移系数定解方程对应的位移系数矩阵.

2） 分岔失稳特征方程

对于分岔失稳，式（19）有非零解的条件是位移系数矩阵行列式为0，即

3） 特征值与临界荷载

由式（20）可求出矩阵A(λ，θ)的特征值λcr，该特征值对应于分岔失稳时的临界轴力为

4） 特征向量与失稳模态

表2 圆曲梁支座边界条件Tab. 2 Support boundary conditions of circular curved beam

3.2 分岔失稳临界荷载与失稳模态

3.2.1 临界荷载结果与分析

根据以上分析方法，选取不同边界约束条件，计算η= 1.0、圆心角 10°～180° 时圆拱的临界荷载系数，并与文献模型相应结果进行比较，结果详见表3所示. 分析表明：

1） 对于两端铰支拱，由于边界条件相同，本文模型所给结果与文献[3,4,6]等模型的结果完全一致；而且采用本文模型可得到前人没有研究过、但工程中应用广泛的跨中单铰拱及两端插支拱的圆拱平面外分岔失稳的临界荷载.

2） 对于两端固支拱（扭固），本文模型和文献[4]结果完全一致，首先是由于两个模型采用了相同定解条件，同时说明圆拱平面外变形分析时采用大变形模型和大位移模型的临界荷载相同；由于采用了相同扭固定解条件和相同位移微分方程简化方法，文献[3-4]简化模型给出了相同的临界荷载；而引入小扭转位移的假定简化微分方程后，临界荷载简化模型计算结果比原模型计算结果大，反映了简化模型的计算结果偏于不安全. 随着弯扭刚度比的越大，简化模型的计算结果偏差越大，表明随着弯扭刚度比增大，拱的平面外扭转变形越大，小扭转位移假设产生的影响越大.

3） 两端固支拱中文献[6]模型与其他模型相比相差较大，且结果偏高，是由于该模型给出的位移方程存在很大的局限性，临界荷载并非源于理论计算，而是采用直梁单元离散圆拱的有限元法，得到了圆拱面外失稳的数值解而非解析解，且屈曲荷载高于理论值.

表3 各类圆拱临界荷载系数Tab. 3 Critical load coefficients of all circular arches

4） 对于两端固支拱，当不考虑约束扭转时，不同固支条件所得临界荷载不同：弯固条件临界荷载较高，全固条件临界荷载过小，扭固约束临界荷载为中间值. 弯固支座直接约束限制了圆曲梁的弯曲位移，弯固条件对拱脚的约束最强，曲梁二阶弯矩减小，临界荷载较高；全固支座导致拱脚扭角为0，放松了对拱面外的扭转约束，扭转及弯曲变形较大，二阶弯矩增大，临界荷载过小，更重要的是，全固支座不适用于自由扭转圆曲梁的分析；文献[3-4]等采用的扭固约束，通过对扭转变形的约束、放松了拱脚面外的弯曲转动约束，弯曲变形只受到了较小的间接约束，临界荷载处于中间值.

5） 不同定解条件计算的临界荷载差异随着弯扭刚度比及圆心角的变化而呈现单调性变化，即弯扭刚度比或圆心角越大，不同条件下的临界荷载差异越大，这是由于圆拱的平面外失稳呈现了圆曲梁的变形特征，而圆曲梁的弯曲和扭转变形是耦合的，圆曲梁扭转会影响弯曲变形，无论是采用哪一类位移的定解条件，均影响到另外一类变形，随着圆心角及弯扭刚度比的增大，圆拱侧扭变形越大，扭转产生的弯曲变形越大，临界荷载的差异随之增大. 综合分析认为，对于自由扭转圆拱，采用扭固定解条件分析圆拱平面外稳定最为合理.

6） 对于弯扭刚度比和圆心角相同的圆拱，当支座为弯固条件时，两端固支拱平面外失稳临界荷载取值时刻保持最大、插支拱次之（两端插支拱与两端固支拱最大相差 -28.72%）、单铰拱再次、两铰拱最小；当支座为扭固条件时，插支拱平面外失稳临界荷载最大、两端固支拱临界荷载次之（两端插支拱与两端固支拱最大相差为19.27%），圆心角较小时，两端铰支拱临界荷载系数小于单铰拱荷载系数，圆心角较大时，结果相反.

3.2.2 失稳模态结果与分析

根据式（13）～（15）及表1，结合各类圆拱平面外分岔失稳的特征及临界荷载系数，计算了η = 1.0时各类圆拱失稳模态，将其中圆心角为150° 时不同模型计算的不同支座条件圆拱失稳模态对比如图2所示.

分析结果表明：

1） 各类圆拱在面内均布径向荷载作用下的平面外分岔失稳模态均为单波对称.

2） 对于两端铰支拱，本文模型与文献[4]的扭角失稳模态及文献[6]的挠度失稳模态完全相同.

3） 对于两端固支拱，本文扭固支座条件下模型与文献[4]的扭角失稳模态完全相同，其原因是采用了相同的定解条件.

4） 对于两端固支拱，不同定解条件圆拱扭转角差异较大. 其中：弯固条件直接约束了曲梁弯曲位移，二阶弯矩减小，扭角最小；扭固条件直接约束了扭转变形，扭角受到一定约束，扭角次之；全固支座放松了对曲梁变形的扭转约束，扭角较大.

图2 圆拱失稳模态对比Fig. 2 Instability mode comparison of circular arch

5） 对于单铰拱，弯固条件支座附近挠度小于扭固条件，可见弯固条件对支座挠度约束较强.

4 圆拱平面外极值点失稳分析

4.1 分析方法

当圆拱结构同时存在面内和面外荷载时，圆拱可能出现平面外极值点失稳. 利用本文模型，给出了圆拱平面外极值点失稳的解析计算方案. 具体步骤如下：

1） 圆曲梁位移

根据截面位移计算公式及定解条件，可得到圆曲梁位移系数定解方程：

式中：A为根据圆曲梁支座x= 0和x=l处的边界条件，由给定位置的位移或变形方程的基函数确定的位移系数矩阵；δq为支座处对应的位移或变形的特解向量；δe为圆曲梁支座位移或变形向量.

由式（24）可得位移系数d为

将位移系数代入式（11）～（12），即可得到其位移方程.

2） 圆拱平面外荷载-挠度曲线

将面外荷载代入式（11）～（12）的特解项，把x取值代入挠度方程（见表1），即可求得圆拱在此面外荷载作用下x处的挠度值；改变面外荷载值，求出挠度，并画出曲线，即可得到面外荷载-挠度曲线. 为清晰表达各物理量之间的关系和坐标，将圆拱位移无量纲化如表4所示.

4.2 圆拱荷载-位移曲线结果与分析

选取直径为 10 m、圆心角φ= 150°、η= 1.0的圆拱，同时对其施加径向均布荷载qz和面外均布荷载qy，分别计算两端固支拱（扭固）、两端铰支圆拱、两端插支拱和单铰拱（扭固）的荷载-位移曲线. 图3给出了不同径向均布荷载作用下圆拱面外均布荷载与面外跨中挠度的关系曲线，其中λ取nλcr，n为临界轴力特征值系数，分别为 0、0.2、0.4、0.6、0.8；图 4 给出了恒定面外均布荷载作用下圆拱径向均布荷载与面外跨中挠度的关系曲线；为反映圆拱径向荷载对面外抗弯刚度的影响，图5给出了圆拱相对径向荷载对面外弯曲刚度的影响曲线.

表4 坐标变量无量纲化Tab. 4 Dimensionless of coordinate variables

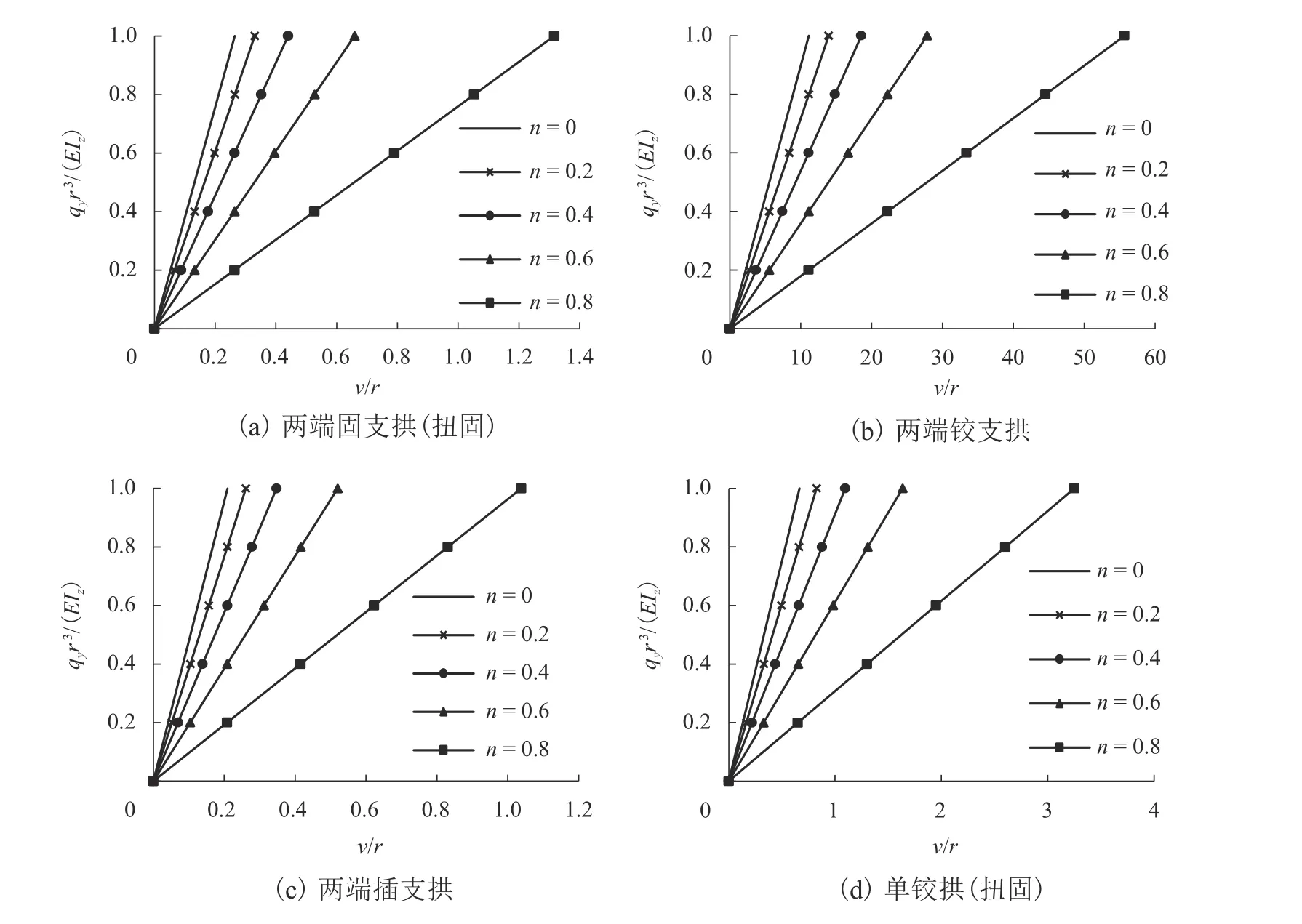
图3 圆拱面外荷载与面外跨中挠度关系Fig. 3 Relationship between out-of-plane load and mid-span deflection for circular arch

图4 圆拱径向荷载与面外跨中挠度关系Fig. 4 Relationship between radial load and out-of-plane deflection at mid-span for circular arch

图5 圆拱相对径向荷载与面外弯曲刚度影响曲线Fig. 5 Influence curve of relative radial load and out-ofplane bending stiffness for circular arch

由图3和图5可以看出：

1） 当径向荷载确定时，面外荷载与面外挠度的关系为线性关系，圆拱径向荷载的存在不改变圆拱面外荷载位移曲线的线性特征.

2） 面内径向荷载的存在，使得拱存在轴力，降低了面外的抗弯刚度，径向荷载对圆拱的弯曲挠度的影响不能忽略.

3） 面外荷载一定时，径向荷载越大，面外挠度越大，圆拱的面外抗弯刚度呈线性规律减小. 当径向荷载达到某一值时，面外刚度为0，发生面外失稳.

产生上述现象的原因是：对于小位移拱，尽管圆拱的面内荷载只产生轴力和面内压弯变形，面外荷载只产生面外弯曲挠度和扭曲变形，但面内荷载产生的轴力增加了面外弯曲的弯矩、从而导致弯曲刚度减小.

由图4可以看出：

1） 面外荷载一定时，圆拱平面外挠度随着径向荷载的增大而增加，且呈非线性关系增加.

2） 径向荷载最大值恰好与圆拱平面外分岔失稳临界荷载相同，这是典型的圆拱平面外失稳问题.

上述现象说明了本文提出的模型考虑了圆曲梁几何非线性，既可以用于圆曲梁的几何非线性位移分析、也可以用于圆拱的平面外稳定分析.

5 结 论

1） 考虑了大位移几何非线性的影响，给出了圆曲梁挠度和扭转角解析解一般格式及相应简化格式，同时得到了圆曲梁变形和内力表达式，且为通用模型；提出了位移基函数向量及导数转换矩阵表达格式，极大方便了圆曲梁位移、变形及内力运算.

2） 基于圆曲梁大位移静力模型及圆拱结构边界条件，对两端铰支拱、两端固支拱、两端插支拱、跨中单铰拱进行分析，建立了圆拱平面外分岔失稳分析的特征方程，得到了圆拱平面外分岔失稳的临界荷载及失稳模态；同时提出了圆拱平面外极值点失稳分析方法，并根据荷载-位移曲线对四种圆拱做了平面外极点失稳分析.

3） 本文建立的圆拱平面外稳定分析方法，可用于复杂拱平面外机动分析，即当稳定特征方程解全为0时，为机构；当稳定特征方程解为非全0解时，为结构.

4） 本模型可用于各种支座条件下圆拱结构在不同荷载作用下的平面外几何非线性静力受力分析及分岔和极值点稳定分析.