极端波浪作用下T梁与箱梁受力研究

杨志莹 ，黄 博 ，段伦良 ，张家玮 ，祝 兵

（西南交通大学土木工程学院，四川 成都 610031）

许多近海桥梁在极端条件下（飓风或海啸）受损是由于飓风或海啸引起的波浪冲击桥梁主梁，造成主梁移位、落梁等. 因此，极端条件下主梁受到的波浪荷载是威胁近海桥梁安全的主要因素之一，研究近海桥梁主梁在极端波浪作用下的受力状态及破坏机理对近海桥梁的设计、施工、维护具有重要意义.

一些学者通过试验研究了极端波浪作用在板式梁[1-2]，T 梁[3-6]以及箱梁[7-9]上的波浪力. French[1]试验研究了在极端波浪作用下，水平平板上的波压力分布情况，但是试验中采用的是有侧板的平板，阻碍了波浪与结构物作用时的越浪行为，也没有考虑极端条件下平板可能浸没于海平面下的情况. Kulin[2]试验研究了处于淹没状态的水平平板在极端波浪作用下平板宽度、水深及波浪振幅对波浪荷载的影响.McPherson[3]进行了一个1∶20的T梁桥在海啸作用下的模型试验，试验中保持模型高度不变，通过改变水深来模拟不同净空高度及淹没深度的工况.Hayatdavoodi[5]对比研究了平板与T梁在海啸作用下的受力，试验共设计133种工况，研究了水深、波高以及淹没深度和抬高高度变化对波浪力的影响.Nakao等[10]研究了1∶20的缩尺桥梁模型上的海啸波浪力，对比了不同的截面形式（矩形截面、梯形截面、倒梯形截面等）对波浪力的影响.

以上研究对跨海桥梁建设起到了极大的推进作用，但是目前相关研究多是针对板式梁桥和T形梁桥，对于我国桥梁建设中应用最广泛的箱形梁桥的研究极少[7-9]. Huang等[9]通过水槽试验研究了在规则波作用下，波高、水深以及淹没深度变化对箱梁波浪力的影响，但是文中未针对两种极端海况（海啸、飓风）下桥梁上部结构受力作研究.

本文主要针对极端条件（海啸及飓风）下近海桥梁主梁毁坏问题，对T形截面主梁及箱形截面主梁进行受力分析，并比较二者受力差异. 采用OpenFOAM建立二维数值模型，首先对数值水槽的造波效果及波浪力计算结果进行了验证. 在此基础上，以孤立波模拟海啸，以椭圆余弦波模拟飓风波浪，分析波高及主梁淹没系数对T梁、箱梁受力的影响，比较二者受力的差异.

1 数值模型

采用OpenFOAM建立二维数值模型. 通过造波模块Waves2Foam分别生成二阶孤立波、椭圆余弦波来模拟实际中的海啸波浪和飓风波浪. 考虑到海啸波和飓风波浪作用下建立的数值水槽尺寸，水槽布置及网格尺寸方面存在差异，为方便下文描述，将海啸波作用下的数值模型称为Ⅰ类模型，将飓风波浪作用下的数值模型称为Ⅱ类模型.

采用的T形主梁尺寸与Hayatdavoodi等[5]实验研究中的T梁模型相同，缩尺比为1∶35，其原型结构为近海桥梁中常见的2车道T形主梁，梁宽10.675 m，梁高1.778 m，箱梁模型根据T梁模型设计，保证两种主梁具有相同的梁宽及梁高，细部尺寸见图1. 计算采用水深d= 0.086 m，考虑3种淹没系数Cs= -0.1，0，0.3. 淹没系数Cs≥ 0代表结构处于完全淹没状态，此时Cs=Z*/d，Z*为静水面到主梁顶板上缘的距离；Cs＜ 0代表结构处于半淹没状态，此时Cs= -Z/d，Z为主梁顶板下缘到静水面的距离，淹没系数示意见图2. 计算工况列于表1.

图1 T梁与箱梁截面（单位：cm）Fig. 1 Configuration of the T girder and box girder (unit： cm)

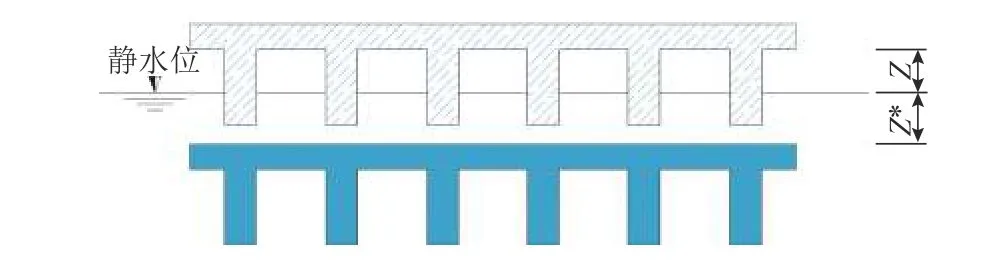
图2 淹没系数示意Fig. 2 Sketch of the submergence coefficient

1.1 控制方程

采用RANS方程及SSTk-ω湍流模型描述流体运动，采用VOF （volume of fluid）法追踪自由液面.假设流体为不可压缩黏性流体，其质量方程和动量方程分别如式（1）、（2）.

SST k-ω湍流扩散方程为()

1.2 边界条件及网格收敛性验证

数值水槽布置如图 3所示，图中，λ1、λ2均为消波区长度. Ⅰ类模型水槽长l = 5 m，高0.172 m，宽0.1 m，Ⅱ类模型l = 20 m，高0.172 m，宽0.1 m. 为了避免形成反射波，在入流边界及出流边界处设置消波区：Ⅰ类模型，λ1= λ2= 1 m；Ⅱ类模型，λ1= 2 m，在出流边界设置的λ2= 3 m.

入口边界上采用根据波浪类型、水深等给定的速度边界条件waveVelocity及相分数边界条件wave-Alpha. 在顶端采用压力进出口边界条件，水槽底面及主梁壁面均为无滑移边界. 本文采用的是二维计算模型，通过将第3个方向（不在此方向上进行求解）上的壁面（前、后）指定为empty边界类型，实现二维数值模型模拟.

为保证计算精度及计算效率，对网格尺寸进行数值收敛测试. 图4为Ⅰ类模型网格数量总数N采用 250 × 9、500 × 17、500 × 29、1 000 × 57、2 000 ×172、3 333 × 172、5 000 × 344 个时，海啸波浪（波高H = 0.3d = 0.025 8 m）作用在箱梁上最大竖向力（）.网格总数数量采用2 000 × 172个时计算结果已满足计算精度，此时网格尺寸为： ∆ x（长）=0.0025m ，Ⅱ类模型由于水槽长度较长，将整个计算域划分为核心区（主梁模型附近6 m ×0.1 m）及非核心区. 对核心区网格尺寸采用同样的测试方法，最终确定核心区网格尺寸为，；非核心区网格尺寸为为了达到数值稳定以及时间计算精度，在保证库朗数小于1的情况下指定时间步长

图3 水槽布置（单位: m）Fig. 3 Sketch of wave flume (unit: m)

图4 网格尺寸变化对箱梁所受海啸竖向力峰值的影响Fig. 4 Variations of horizontal wave force versus different mesh sizes

1.3 模型验证

将无主梁结构时水槽中点处（距水槽左端l/2）的波面曲线与波面理论解[11-12]进行对比，以验证数值水槽造波效果，结果如图5所示（仅给出H = 0.3d =0.025 8 m的波面对比）. 由图5可见，数值解与理论解吻合良好，且波面稳定，说明数值水槽造波效果良好.

基于Hayatdavoodi等[5]开展的孤立波与T梁相互作用的实验研究，选用工况：d = 0.086 m，Cs= 0.2，H = 0.025 8 m，验证数模波浪力计算结果的准确性.将计算得到的波浪力与Hayatdavoodi的试验结果进行对比，如图6所示，图中，FH、FV分别为水平力和竖向力. 水平力峰值和竖向力峰值与试验结果吻合良好. 水平力谷值由于受到越浪、尾涡等非线性因素的影响，数值结果与试验结果之间存在微小的差异.竖向力谷值间也存在微小的差异，这是由于试验中水槽实际宽度（垂直于波浪传播方向）为0.152 m，主梁的宽度为0.149 m，水槽壁面与结构物之间存在空隙，使得试验结果与二维数值模型结果稍有差异. 总体上，数值结果与试验结果基本吻合，相对误差较小，说明RANS方程及SSTk-ω湍流模型可以准确模拟波浪与桥梁主梁的相互作用过程.

图5 波面数值解与理论解对比Fig. 5 Comparison of water elevation between numerical results and the theoretical results

图6 波浪力数值解与试验值对比Fig. 6 Comparison of wave forces between numerical results and experimental data

2 计算结果

本文给出的FH和FV均为沿水槽宽度方向每延米的二维结果（主梁宽度方向为垂直于纸面方向），且为方便比较不同淹没深度对波浪力的影响，竖向力均扣除静水浮力.

2.1 海啸波浪

图7为H= 0.5d时，T梁与箱梁的波浪力时程曲线. 对于竖向力FV：当主梁完全淹没时（Cs= 0.3，0），T梁与箱梁的竖向力在整个海啸冲击过程中基本相同，此时竖向力主要由波浪对主梁持续作用产生的准静力组成，因此可以认为主梁截面形式对竖向准静力影响较小；当主梁半淹没时（Cs= -0.1），T梁竖向力曲线较光滑，而箱梁的竖向力在峰值处有尖峰. 这一现象同样可以在H= 0.2d～0.4d的工况中观察到，而H= 0.1d时，箱梁竖向力无明显尖峰. 这是由于未完全淹没时，竖向力还受到波浪表面能量传递对主梁产生的冲击作用影响. 箱梁由于悬臂长度更长，波高较大的（H= 0.2d～0.5d）海啸冲击箱梁顶板下缘使其竖向力有尖锐的峰值.

对于水平力FH，不同淹没深度下T梁的水平力峰值均大于箱梁. 图7（c）中时刻a、b对应的主梁-海啸相互作用过程分别如图 8（a）、（b）所示. 主梁水平力主要由两部分组成：一是主梁前、后侧液面差产生的静水压力差；二是由于主梁阻碍了水质点水平运动，水质点作用于主梁的上动水压力. 时刻a波峰到达主梁顶板前缘，主梁前、后侧液面差在此时刻接近最大，同时波峰位置处的水质点水平速度较大，对主梁的动水压力较大，二者叠加，水平力在此时刻达到峰值. T梁腹板与箱梁腹的板构造差异是造成二者水平力峰值差异的主要原因. T梁腹板位置接近顶板前缘位置（在x方向上），运动水质点直接作用于腹板上，箱梁腹板前存在空区（如图1所示），使作用于箱梁腹板上的动水压力小于T梁腹板上的动水压力. 同时箱梁腹板倾斜，作用于腹板上波浪力产生竖向分力，进一步减小了箱梁的水平波浪力. 因而箱梁总的水平力峰值明显小于T梁水平力峰值. 时刻b由于主梁后侧液面较高，主梁受到的水平力表现为负值（与波浪传播反向）.

图7 海啸作用下T梁与箱梁波浪力时程Fig. 7 Time series of tsunami wave forces on T girder and box girder

图8 海啸波与T梁及箱梁相互作用过程Fig. 8 snapshots of solitary wave and superstructure interaction

由图 9（b）可知: 在 Cs= 0.3，-0.1 时，T 梁与箱梁的水平力谷值随波高增大而增大；Cs= 0，波高增大到H = 0.5d时，由于顶板位于静水面位置，随着波峰传播至顶板上，水深变小而波高较大，会导致波浪破碎，进而造成波能损耗，波浪力不再持续增加反而减小；与图9（a）相比，T梁、箱梁受到的水平力谷值为相应工况下水平力峰值的1/3～1/2，水平力谷值对主梁造成的威胁较小.

T梁与箱梁的竖向力峰值（图9（c））随波高增大而增大，且淹没系数越小，竖向力峰值越大. 如上所述，当主梁完全淹没时（Cs= 0.3， 0），竖向力主要由准静力组成，主梁截面形式对准静力的影响较小.半淹没时（Cs= -0.1），竖向力峰值主要由准静力和冲击力组成，由于箱梁顶板悬臂长度更长，较大波高（H = 0.2d～0.5d）的海啸冲击箱梁顶板，使其竖向力峰值大于T梁，最大差值接近T梁竖向力峰值的13%. 因此，对箱形截面主梁的跨海桥梁应加强其竖向约束.

T梁与箱梁的竖向力谷值（图9（d））主要由波浪爬高、越浪等产生，因此波高越大、淹没系数越大时，竖向力谷值也越大. 在Cs= -0.1时，箱梁的竖向力谷值略大于T梁竖向力谷值，说明箱形截面主梁更易发生波浪爬高及越浪.

图9 海啸作用下箱梁与T梁受力Fig. 9 Tsunami induced wave forces on T girder and box girder.

综上，对于海啸易发海域内的近海桥梁，若主梁截面形式为T形，则应加强其水平约束，若主梁截面形式为箱形，则应加强其竖向抗冲击约束.

2.2 飓风波浪

与海啸波作用结果相同，主梁完全淹没（Cs=0.3，0）时，T梁与箱梁的波浪力时程变化特征基本相同，在主梁半淹没（Cs= -0.1）时，T梁的竖向力时程曲线较光滑，箱梁的竖向力在峰值处有明显的尖峰（如图10所示），即冲击作用对箱梁竖向力影响较大. 值得注意的是，在飓风波作用下，尽管箱梁受到明显的冲击作用，但其竖向力峰值却小于T梁的竖向力峰值.

不同工况下，T梁、箱梁的波浪力峰值、谷值见图11（在计算时长范围内，波浪力会随着波浪周期出现多个峰值与谷值）.

图10 T梁和箱梁在Cs = -0.1时受飓风波浪力的时程曲线（H = 0.3d）Fig. 10 Time-histories of hurrican wave forces on T girder and box girder when Cs = -0.1，H = 0.3d

由图11（a）可见: T梁及箱梁的水平力峰值都随波波高增大而增大；T梁水平力峰值受淹没系数的影响较小，在3种淹没系数下几乎接近，箱梁水平力峰值在淹没系数Cs= 0.3时最大；相同工况下，箱梁的水平力峰值小于T梁，最大差值接近箱梁水平力峰值的31%；飓风波作用产生的水平力谷值与峰值在数值上接近，应当考虑水平力谷值对主梁安全性的威胁；T梁、箱梁的水平力谷值也随波高增大而增大，淹没系数较大时，水平力谷值较大.

图11 飓风作用下箱梁与T梁受力Fig. 11 Hurricane induced wave forces on box girder and T girder

T梁与箱梁的竖向力峰值（见图11（c））在Cs=0，0.3时接近. Cs= -0.1时箱梁的竖向力峰值小于T梁竖向力峰值，且在波高较小（H = 0.1d，0.2d）时，二者的差值更大，随着波高增大，箱梁由于顶板悬臂长度更长，较大波高的波浪冲击顶板下缘使其与T梁竖向力峰值间的差值缩小. T梁、箱梁（图11（d））的竖向力谷值随波高增大而增大，且淹没系数越大，竖向力谷值越大. 原因如2.1节所述.

综上，对于飓风易发海域内的近海桥梁，若主梁为T形截面应加强其水平、竖向约束，若主梁为箱形截面，应加强其竖向抗冲击约束. 相比于飓风波对主梁的作用力，波高较大时，海啸波对主梁的作用力更大，如H = 0.4d，Cs= 0.3时，海啸作用于T梁的水平力峰值约为飓风波作用于T梁的水平力峰值的2.0倍，H = 0.4d，Cs= -0.1时，海啸作用于箱梁的竖向力峰值约为飓风波作用于箱梁的竖向力峰值的1.8倍.

3 结 论

以上的分析结果表明: 海啸波作用下，T梁与箱梁受到的水平力峰值、谷值及竖向力峰值、谷值总体上随波高增到而增大（Cs= 0，H = 0.5d例外）；淹没系数越大（仅针对本文研究范围内的淹没系数Cs=0.3，0，-0.1），水平力峰值越大；相同工况下，箱梁的水平力峰值小于T梁，最大差值接近箱梁水平力峰值的32%，因此对海啸易发海域内的T形截面主梁应加强其水平约束. 水平力谷值是相应工况下峰值的1/3～1/2，对桥梁的安全威胁较小. 受冲击力的影响，T梁与箱梁的竖向力峰值在淹没系数较小（Cs=-0.1）时最不利，且箱梁竖向力峰值大于相应工况下T梁的竖向力峰值，因此对海啸易发海域内的箱形截面主梁应加强其竖向抗冲击约束.

飓风波作用下：T梁与箱梁受到的水平力峰值、谷值及竖向力峰值、谷值同样随波高增大而增大；T梁的水平力峰值受淹没系数的影响较小，箱梁的水平力峰值在淹没系数Cs= 0.3时最大. 相同工况下箱梁的水平力峰值小于T梁，最大差值接近箱梁水平力峰值的31%；水平力谷值在淹没系数较大（Cs=0.3）时不利；受冲击作用的影响，竖向力峰值在淹没系数较小时更不利，波高较小时箱梁的竖向力峰值小于T梁，随着波高增大，箱梁的竖向力峰值与T梁接近；淹没系数越大时，T梁与箱梁的竖向力谷值越大.

与飓风波对主梁的作用力相比，波高较大时，海啸波对主梁的作用力更大.