高低温下复合绝缘子的连接抗拉性能及优化

晏致涛 ，马文俊 ，张 璞 ，裘 哲

（1. 重庆科技学院建筑工程学院，重庆 401331；2. 重庆大学土木工程学院，重庆 400044）

复合绝缘子的金具和玻璃芯棒的滑脱破坏是高压输电线路上经常遇到的问题. 绝缘子端部金具的预紧应力大小在影响复合绝缘子抗拉性能中起决定性作用，过大的预紧应力也会造成玻璃芯棒的径向应力过大而导致芯棒的脆性破坏，而在同样的预紧应力大小作用下，预紧应力的分布也是影响复合绝缘子抗拉强度的主要因素之一，所以对复合绝缘子端部金具做预紧应力分布优化分析是很有必要的.

国内外对复合绝缘子的力学性能进行了研究：徐如恬等[1-3]对绝缘子中的瓷材料强度做了对比分析，从绝缘子芯棒的强度入手研究复合绝缘子的受力性能；张硕等[4-5]进一步研究了单向玻璃纤维增强环氧树脂复合材料的力学性能和低温收缩率；Paris等[6]对复合绝缘子在持续荷载作用下的力学性能进行了试验分析；Demidov等[7]通过对绝缘子的基体硬度值及涂层与基体的复合硬度值进行了评价；De Tourreil等[8]对3种不同设计的高压复合绝缘子在长时间断裂失效情况下做了对比分析.

由于复合绝缘子材料本身的力学性能并不起决定作用，更多的研究者开始关心接头和压接工艺：余涛等[9]提出了金具滑脱是绝缘子破坏的主要形式；袁骏[10]提出1 000 kV的复合绝缘子应采用压接式结构来满足机械性能要求；钟万才[11]进行了绝缘子拉力试验，发现U型连接头设计裕度不足；杨祉豪[12]进行了绝缘子夹头的有限元分析；陈显贻等[13]对多种复合绝缘子金具和芯棒在不同连接结构和机械强度下做了对比试验分析；谢占山等[14-15]发现复合绝缘子疲劳损伤首先是由芯棒与金具接触外表面开始，发生在金具与芯棒连接过渡区；Kumosa等[16]认为绝缘子失效的原因主要是由于绝缘子金具的不当压接引起玻璃芯棒脆性破坏及金具和玻璃芯棒之间发生滑移引起的结构失效.

可见，目前对复合绝缘子力学性能的研究主要集中在绝缘子芯棒的受力破坏以及压接试验，很少有研究针对绝缘子在高低温作用下的力学表现，为此，本文针对复合绝缘子破坏形式中最常见的滑移破坏进行了数值模拟和分析，进一步进行了端部金具预紧应力优化，并就高低温环境下的绝缘子力学性能做了对比分析.

1 典型压接复合绝缘子受拉试验

以常规电压22 kV输电线复合绝缘子为例，进行了复合绝缘子的高低温下受拉试验. 试验采用Instron1186电子万能试验机，通过位移控制进行材料力学性能试验，研究复合绝缘子分别在高低温作用下的抗拉性能. 绝缘子的压接实物如图1（a）所示，端部金具的预紧应力沿环向分为8段均匀分布在金具端口处，如图 1（b）. 图中：z、r、φ 为柱坐标，分别代表轴向、径向和扭转向；σr、σz分别为径向和轴向正应力.

图1 复合绝缘子Fig. 1 Composite insulators

图2 为不同温度下复合绝缘子受拉后的破坏形态. 由图2可以看出，不同温度下，复合绝缘子的破坏形式均不是由于玻璃芯棒达到荷载强度极限发生破坏引起的，而是在未达到强度之前，金具与玻璃纤维芯棒之间产生滑移，导致端部金具与芯棒拉脱导致结构失效.

图2 不同温度下试样端口破坏实物Fig. 2 Specimen of damage at different temperatures

图3 为不同温度下试样拉力位移曲线，由图3可以看出，无论是高温还是低温，和常温相比，复合绝缘子的承载力和延性均降低，尤其是高温状态，承载力和延性均大幅降低.

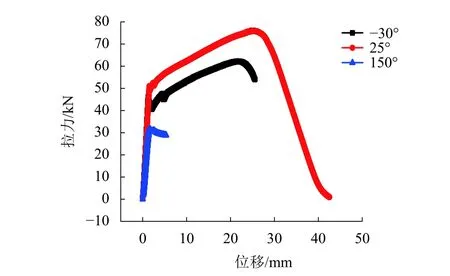
图3 不同温度下试样拉力位移曲线Fig. 3 Tension of specimens with respect to displacement at different temperatures

常温和低温下复合绝缘子的拉伸力学试验本质上可归结为3个阶段：荷载上升阶段，荷载达到峰值后持续增大的强化阶段，结构金具与芯棒产生滑移后荷载下降阶段. 而高温下的复合绝缘子在经过荷载上升阶段后，没有明显的强化阶段，而是直接出现金具与芯棒滑移的现象，这种现象是由高温引起金具与芯棒之间的粘结性能大幅度减弱造成的.

2 常温下复合绝缘子力学性能数值模拟

2.1 模型参数

根据厂家提供，金具力学性能参数如表1所示，假定为各向同性材料，采用多线性随动强化模型模拟金具在压接过程中的材料非线性. 绝缘子玻璃芯棒假定为各向异性线弹性材料，力学参数如表2所示.

表1 Q235碳素结构钢金具力学性能Tab. 1 Mechanical properties of Q235 carbon steel fittings

表2 单向玻璃纤维增强环氧树脂力学性能Tab. 2 Mechanical properties ofunidirectional glass fiber reinforced epoxy resin

通过ANSYS有限元软件建立仿真模型，对其进行相关分析. 整体模型采用SOLID95单元，芯棒表面接触单元采用TARGE170单元，金具表面接触单元采用CONTA174单元，接触刚度取值0.1 kN/m，最大穿透值取值0.2，面-面接触单元本构采用库仑摩擦模型，接触界面上的√最大接触摩擦应力τmax取值为钢材屈服强度的. 金具与芯棒之间的摩擦系数通过与实验结果不断对比计算后，在常温下为0.320，低温-30 ℃ 下摩擦系数为 0.286，高温 150 ℃下摩擦系数为0.230. 其中芯棒长度为70 mm，直径为24 mm，模型网格沿径向均分32段，沿轴向均分10段进行划分，端部金具长度为35 mm，外径为32 mm，内径同芯棒，模型网格沿径向均分32段，沿轴向均分20段进行划分.

2.2 模型工况与模拟结果

绝缘子受拉力学性能模拟工况分为2步，第1步：模拟4个沿径向预紧应力分布工况，固定住芯棒两端位移并对其施加预紧应力. 本文施加预紧应力大小的方法是沿径向对金具施加同等大小的径向位移，即等同于施加同样大小的预紧应力，通过计算得到最大径向应力为86.9 MPa（对应最大的摩擦应力为26.07 MPa）. 第2步：从中选出抗拉性能最优工况后再对其取不同的轴向预紧应力分布，重复上述模拟步骤，从中选出最优工况作为端部金具的优化预紧应力备选.

2.2.1 不同径向分布预紧应力模拟工况

工况1：如图4（a）所示，将预紧应力沿径向均匀分布为8块区域，沿轴向分布至距金具端口17.5 mm（金具端部长度的一半）处，此工况为现有厂家生产复合绝缘子的真实状态.

工况2：如图4（b）所示，将预紧应力沿径向均匀分布为4块区域，沿轴向分布至距金具端口17.5 mm处.

工况3：如图4（c）所示，将预紧应力沿径向均匀分布为3块区域，沿轴向分布至距金具端口17.5 mm处.

工况4：如图4（d）所示，将预紧应力沿径向均匀分布，沿轴向分布至距金具端口17.5 mm处.

2.2.2 不同径向分布预紧应力模拟结果

由图5的拉力位移曲线可以看出：在预紧应力大小一样的情况下，工况1的弹性极限荷载大小为52.166 kN，与实验结果的51.341 kN非常接近，而工况4的弹性极限荷载大小为54.961 kN，抗拉表现最优，其次工况1、2、3的弹性极限对应的拉力分别为 52.166、51.886、49.157 kN，抗拉表现最差；4种工况在弹性阶段与实验结果极为接近，但是在非线性阶段与实验结果有一些偏差，这是由于在拉伸实验中，绝缘子在拉力作用下横截面减小使得夹具与绝缘子之间松动而产生了滑移，同时实验中的绝缘子的质量分布不是很均匀也是一部分原因.

图4 不同径向分布预紧应力工况Fig. 4 Preload condition of different radial direction distribution

图5 拉力-位移曲线（工况1～4）Fig. 5 Curves of tension-displacement (case 1- 4)

2.2.3 不同轴向分布预紧应力工况模拟

进行工况5～8的有限元建模和分析，主要考虑不同轴向分布预紧应力情况，如图6.

工况5：如图6（a）所示，将预紧应力沿径向均匀分布，沿轴向分布距金具端口0～8.75 mm处（0～1/4金具长度）和 17.50～26.25 mm 处（1/4～1/2 金具长度）两部分.

工况6：如图6（b）所示，将预紧应力沿径向均匀分布，沿轴向分布距金具端口8.75～26.25 mm处（1/4～3/4金具长度）.

工况7：如图6（c）所示，将预紧应力沿径向均匀分布，沿轴向分布距金具端口0～35.00 mm处（预紧应力覆盖整个金具表面）.

工况8：如图6（d）所示，将预紧应力沿径向均匀分布，沿轴向分布距金具端口处（0～3/4金具长度）.

图6 不同轴向分布预紧应力工况Fig. 6 Preload condition of different axial direction

2.2.4 不同轴向分布预紧应力模拟结果

从图7所示的拉力位移曲线可以看出：在预紧应力大小一样的情况下，工况7的弹性极限荷载最大，为58.610 kN，然而其曲线并不像其他工况一样在结构达到弹性极限后还保留着屈服阶段，而是直接出现了结构的失效，这是由于预紧应力覆盖了整个金具表面，导致金具与芯棒之间产生了滑移，而没有完全覆盖预紧应力的结构模型，其在拉伸过程中，芯棒没有受到预紧应力处的部位在被后端有预紧应力部分的金具挤压后造成形状的变形，使得芯棒与金具接触表面形状变得不连续，故产生了弹性极限荷载后的屈服阶段，所以工况7不可取；工况5的弹性极限荷载大小为53.127 kN；工况6的弹性极限荷载大小为54.512 kN；工况8的弹性极限荷载大小为56.46 mm；工况5、6、8存在材料强化阶段，相较而言，工况8为最优工况.

图7 拉力-位移曲线（工况5～8）Fig. 7 Curves of tension-displacement (case 5 - 8)

3 最优的预紧应力范围分析

从以上数值分析对比结果可知，当预紧应力沿径向均匀分布于金具且不完全覆盖金具的整个内面时（预留一定长度的无预紧应力区间），绝缘子的抗拉性能表现最优，现就绝缘子的无预紧应力区间做进一步分析，以得出最优的无量纲绝缘子预紧应力区间范围，如图8.

工况9：预紧应力沿径向均匀分布于金具表面，沿轴向预留距金具端部3.00 mm的无预紧应力区间.

工况10：预紧应力沿径向均匀分布于金具表面，沿轴向预留距金具端部6.00 mm的无预紧应力区间.

图8 不同无预紧应力预留长度工况Fig. 8 Reserved lengths of different non pre-tightening force

图9 为模拟的拉力-位移曲线，由图9可以看出：工况9位移达到3 mm左右时，曲线开始出现下降，这是由于金具拉出无预紧应力区间后与芯棒之间产生了滑移；工况10的弹性极限荷载大小为56.690 kN，与工况8的弹性极限荷载56.460 kN十分接近，综合最优. 综上可以做出判断，当预紧应力大小恒定时，无预紧应力区间长度占金具整体长度的18%～25%时为最优.

图9 模拟拉力-位移曲线（工况8～10）Fig. 9 Curves of tension-displacement (case 8 - 10)

4 高低温下的绝缘子抗拉性能模拟

进一步对最优工况10进行高低温有限元模拟，并与实验数据和工况1进行对比，如图10. 从图10可以看出：当处于150° 时，试验的弹性极限荷载为31.486 kN，其后拉力位移曲线并不像常温时一样有上升的强化阶段，而是出现了下降形式的强化阶段，这是由于随着温度的升高，金具与芯棒的黏结性能迅速减弱；模拟求得工况1弹性极限荷载大小为32.344 kN，与实验结果基本符合，而工况10的弹性极限荷载大小为32.890 kN，与工况1差距很小.

图10 150 ℃时拉力-位移曲线Fig. 10 Curves of tension-displacement at 150°

图11 为低温下最优压接方式和现有试验数据对比. 由图11可知：当处于-30° 的低温状态下时，实验的弹性极限荷载为47.890 kN，模拟求得工况1弹性极限荷载大小为48.676 kN，与实验结果基本符合；而工况10的弹性极限荷载大小为51.212 kN，相较于工况1大了2.536 kN，增大了5.2%.

图11 -30 ℃时拉力-位移曲线Fig. 11 Curves of tension-displacement at -30°

5 结 论

为研究不同温度下的金具预紧应力模型对绝缘子抗拉性能的影响，结合试验和数值模拟对复合绝缘子进行了拉伸力学性能研究，得出如下结论：

1） 复合绝缘子破坏荷载取决于金具与芯棒的预紧应力大小，其破坏特征主要是金具与芯棒之间产生滑移. 无论是高温和低温，复合绝缘子的受拉承载力和延性均大幅降低.

2） 在预紧应力大小不变的情况下，金具预紧应力的分布情况对复合绝缘子的抗拉强度有很大的影响. 在采用库伦摩擦模拟计算情况下，绝缘子金具的预紧应力为沿径向均匀分布压力，无预紧应力分布区间长度宜定为金具整体长度的18%～25%，此时绝缘子抗拉性能表现最优. 在常温状态下，最优模型的弹性极限荷载较工况1（真实厂家工艺模拟工况）大了8.23%.

3） 当温度在150 ℃时，最优模型的抗拉性能相较于工况1并没有很显著的提升效果，说明在高温下，预紧应力分布的影响对绝缘子抗拉性能的影响相对较小.

4） 在-30 ℃的低温环境下，最优模型的弹性极限荷载较工况1大了5.2%，表明低温也会略微削弱压接优化效果.