改性橡胶隔震支座抗拉性能试验研究*

杜杰伟 潘文 王星然 金昱成

(1.昆明理工大学公共安全与应急管理学院学院 昆明 650000； 2.昆明理工大学建筑工程学院 昆明 650500； 3.云南省抗震工程技术研究中心 昆明 650500)

0 引言

随着我国城市化建设不断加快，众多高层建筑也相继出现，但隔震技术却难以运用到高层建筑上，由于隔震支座自身竖向抗拉性能有限，隔震支座较难在高层建筑中被广泛应用。同时高层建筑由于高宽比一般很大，建筑自身的倾覆力矩也会很大，从而使隔震支座承受较大的竖向拉力，支座抗拉性能难以满足要求。

一般解决支座抗拉问题的方法，可以通过调整上部结构设计方案、设置半主动控制系统、加装抗拉装置和改进橡胶的材料配方等措施来提高隔震支座的抗拉性能。如大阪DT办公楼是采用一种直线轨道滑动隔震支座进行隔震设计的，竖向极限抗拉的承载力可达到18 000 kN[1]。但由于对直线轨道滑动支座的相关研究较少，且生产该种支座的技术要求较高和厂商较少，支座的造价也较其他支座高昂，在工程中应用具有一定难度。除了上述方法外，可以通过改进支座的橡胶材料配方，提高支座自身的抗拉性能来抵抗支座拉伸破坏，如东京衫并花园城[2]采用了1种改性橡胶抗拉隔震支座，支座可以承受到2.5 MPa以上的拉应力。因此通过改进橡胶配方提高隔震支座抗拉性能，抗拉性能较一般隔震支座会有所提升。

1 隔震支座的竖向性能

1.1 隔震支座的竖向刚度

当拉应力作用在隔震支座上超过支座承受能力时将会影响其力学性能，导致结构不能达到预期的隔震效果和抗震目标。为确保在罕见地震下隔震结构的稳定与安全，在隔震支座受拉后，支座的水平性仍应不发生过大变化。同时由于隔震建筑的倾覆力矩会因支座受拉变形而增大，在隔震支座出现水平位移时，应具有一定的拉伸刚度确保支座不产生竖向较大的变形。

一般情况下，在没有剪应变的作用条件下，支座受拉刚度为支座受压的刚度的10%左右。当有剪应变作用时，支座发生水平位移，此时支座拉伸变形量会较大，因此，对隔震支座的竖向拉伸刚度的变化要更为准确的了解。在水平变形条件下，与支座受拉时的竖向刚度相关的力学模型一般有以下4种：

(1)重叠面积法认为支座在拉条件下与支座在压剪条件下的力学行为相似，支座竖向拉伸刚度Kve的计算公式为

(1)

式中,A为支座橡胶的截面面积；Ae为隔震支座有效承载面积；Kv为支座竖向刚度。

但支座在受到拉剪作用时与支座在受到压剪作用时的应力在分布上有所区别。支座在受到压剪作用时，压力大多数会分布在支座上表面与下表面相交的区域；而在支座受到拉剪作用时，支座中未重叠的区域也会承受一部分拉力的作用。因此，当支座水平向产生较大变形时，采用重叠面积法确定支座受拉时的竖向刚度与实际情况会有较大误差。

(2)缩减面积法[3]认为，当支座发生水平位移，支座处于受拉状态时，支座的竖向刚度Kve与纯拉时支座的刚度的确定方法相似，计算公式为

(2)

式中，γ为支座发生的剪切应变；A为支座橡胶约束面积；Aγ为支座在水平应变为γ时的重叠面积；Kv0为纯拉条件下的竖向刚度。

缩减面积法的计算方式虽然简单，但这种方法没有较严格的理论推导，并且没有给出支座在竖向与水平同时产生位移时，支座受拉时竖向刚度的变化规律。

(3)KOH C G等[4]、闫维明等[5]基于双弹簧模型，分析了支座处于拉剪状态时的性能，如图1所示。

该模型采用1个刚性体、1个线弹簧及1个转动弹簧模拟隔振支座，假设高度为1，线弹簧及转动弹簧刚度分别为KH、Kθ。采用2个滚珠为隔震支座提供水平变形。当剪力F与拉力P作用在该隔振支座模型时，刚性体将发生转动，此时转角大小为θ，刚形体下端发生大小为S的水平变形，上端发生大小为u的水平变形，竖向产生的位移为v。杨维国等[6]对双弹簧模型的竖向拉伸刚度计算方法进行了修正，进一步减小了竖向拉伸刚度的计算误差。

(4)党育等[7]基于Haringx模型(见图2)，推导了在发生水平变形时，隔震支受拉时的竖向刚度。此模型将支座看作下部固接的梁，上部在水平方向可以移动，但不能发生转动。在剪力T、弯矩M和拉力F共同作用下，支座受拉时的竖向刚度通过不同拉力分别进行计算。但该计算方法是假设在小变形条件下推导的，当支座受到剪切发生较大变形时，可能存在较大误差。

1.2 隔震支座的拉应力设计值

为确定隔震支座拉应力设计值，一般从两个方面进行分析，一方面是通过支座所能承受的拉应力极限值来限制隔震支座的拉应力。在2001年版的《抗规》中规定：处于罕震作用下的支座不宜有拉应力的出现，而在2010年版的《抗规》中规定：在地震作用下，支座受到的拉应力应小于1 MPa。此规定对支座拉应力进行了限制，主要是因为：①橡胶材料在受拉后其内部会出现损伤，导致支座的弹性降低；②支座受到拉应力后，上部结构会存在倾覆的危险;③在广州大学工程抗震研究中心进行的橡胶支座的抗拉性能试验中，支座的极限拉应力为2～2.5 MPa；④美国相关规范中，支座容许的拉应力为1.5 MPa。日本桥梁设计规范[8]中，规定处于罕遇地震作用下隔震支座的拉应力不应大于2 MPa，欧洲结构设计规范[9]中，规定支座在地震作用下不应受拉。因此，需要对隔震支座受到的拉应力进行限制，避免对上部结构和支座本身造成不利影响。周福霖院士指出[10]，当隔震支座处于偏心受拉时，由于支座会出现复位弯矩，支座最终将处于轴向受拉状态或者发生轴向受拉破坏，支座所受的拉伸承载力主要是轴向拉伸。但当支座受水平剪切发生较大变形时，支座橡胶层的外边缘可能会出现拉应力，导致隔震支座发生拉伸破坏，因此支座的拉应力设计值需要留有一定的安全余量，确保隔震支座仍能为结构提供隔震效果。周福霖院士建议，隔震支座的拉应力应控制在拉应力极限值之前，且支座的容许抗拉强度应控制在屈服点之前。根据隔震支座拉伸应力-应变曲线，如图3所示，支座拉应力的极限值与屈服值的比值约为2.5，而《建筑抗震设计规范》(GB 50011—2010)[11]中确定隔震支座受拉限值的方法与根据隔震支座受拉极限值来确定支座所受拉力的限值类似，即通过取1个安全系数来对隔震支受拉极限值进行折减，从而确定支座容许抗拉强度，而该安全系数的取值为2.5。

另一方面，确定隔震支座拉应力设计值是通过限值隔震支座的竖向位移来确定支座的抗拉强度，从而控制倾覆力矩。在日本的一些高层隔震建筑中，是根据3%的支座高度对支座的受拉变形进行限制。在日本建筑设计规范中，是根据支座拉应变的5%对支座的拉应力进行控制[12]。

根据一些相关的振动台试验，虽然隔震支座在受拉时水平产生较大位移，支座受拉的竖向应变达到了20%～40%，支座也未发生失效仍能工作。但由于抗拉性能方面的相关实验较少，因此隔震支座的拉应力设计值仍然是根据安全系数法或容许应力法等经验方法确定的。

刘文光等[13]基于Haringx理论，在支座处于拉伸状态下，根据支座水平刚度趋近于零的临界条件推导出隔震支座处于纯拉状态下，修正了支座在受拉屈服后的刚度，得到支座受拉的界限拉应力，如图4所示，虚线为根据推导得到的拉应力界限值。

根据理论及支座拉伸剪切试验的结果[13]，支座受拉的临界值均大于支座受拉的屈服值。根据隔震支座在拉伸屈服后的拉力与变形的关系[14]，当支座受拉屈服后，卸载后再对支座进行加载，支座将比初次屈服前更快达到屈服状态，支座的拉伸刚度出现降低，如图5所示。刘文光通过对拉伸试验结果分析，提出了3G原则，建议支座的设计拉应力界限值可控制为3倍支座所用橡胶材料的剪切弹性模量，此时支座受拉不会发生过大剪切变形，支座仍可以提供一定的刚度，减少对建筑的影响。同时，在隔震支座受拉后，拉伸应变可控制在10%以内，从而减小支座竖向拉伸变形对隔震结构的影响。

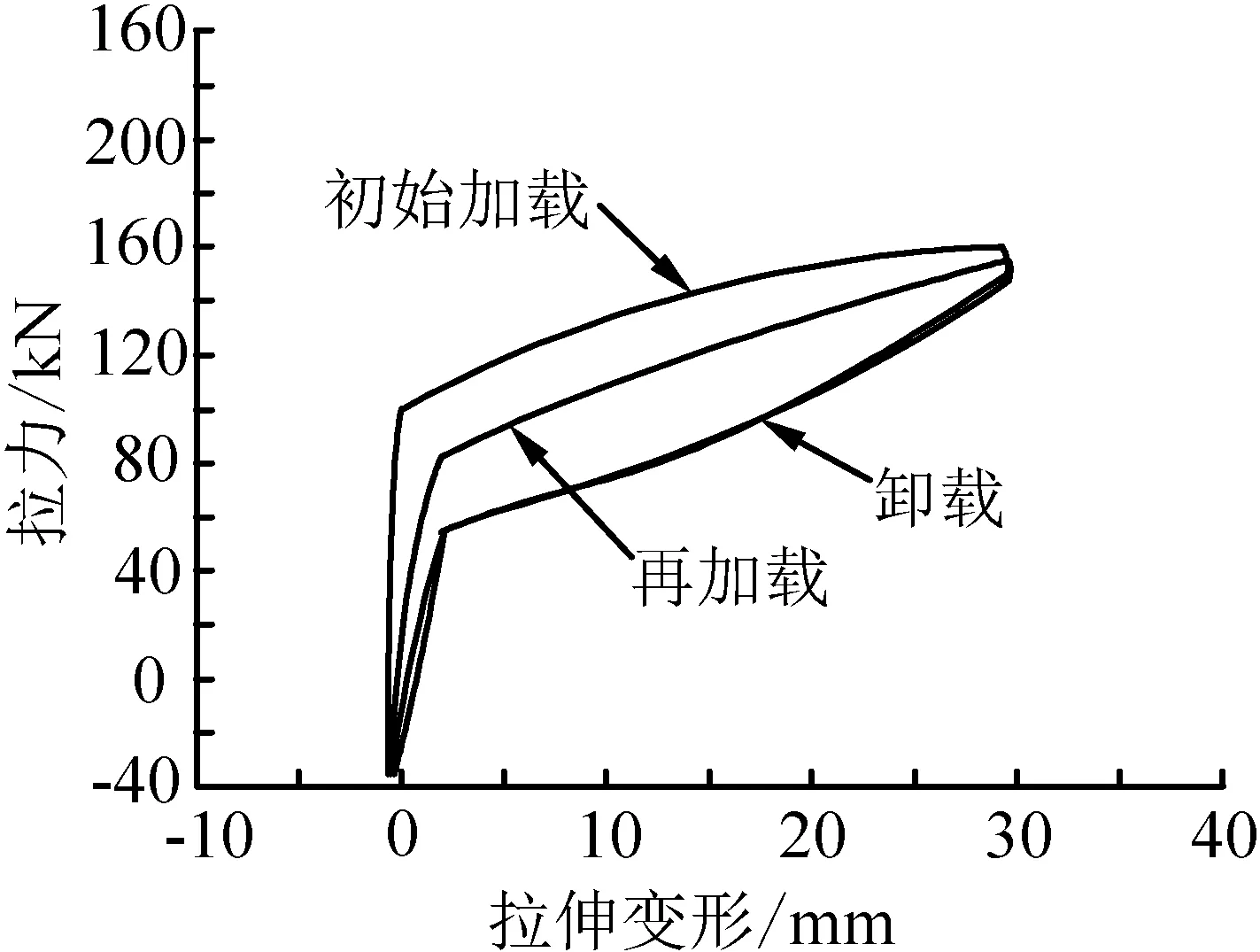
图5 支座屈服前后拉力变化

当隔震支座受拉且拉力大小超出一定范围后，支座橡胶内部会出现负压而导致橡胶内部产生空洞，此时支座虽然不会破坏，但此时橡胶内部产生的损伤会对支座的水平性能造成不利影响，虽然在隔震结构中只会出现较少数量的隔震支座的性能改变，对结构整体影响不明显，但是结构仍存在一定的安全隐患。如果能确保隔震支座在罕遇地震作用下不会出现较大损伤，即罕遇地震作用下支座在受拉状态时处于弹性阶段，支座就有一定的安全储备，在极罕遇地震作用下能保证上部结构的安全。因此为确保隔震支座在受拉时，力学性能不出现较大变化，可将隔震支座的拉应力设计值控制在支座的屈服拉应力之前。

隔震支座作为隔震建筑中的一个重要部分，其安全等级比较高，但在《建筑结构可靠性设计统一标准》[15]中，与构件相关的重要性系数取值仍是1.0，同时支座在受到竖向压力作用时自身的剪切模量也会受影响，但支座设计压应力在一定程度上已将建筑的重要性等级考虑在内，因此隔震支座的屈服拉应力依据橡胶支座的相关规范[16]进行确定，也在一定程度上考虑了建筑重要性等级。杨维国等[6]通过有限元模拟和橡胶隔震支座拉伸性能试验[17]进行对比验证，对环形橡胶支座的竖向拉伸刚度计算式进行修正后，发现隔震支座在水平发生的位移达到规范限值(u=0.55D)时，支座竖向受拉状态时竖向刚度约为零剪应变下支座在受拉状态时竖向刚度的一半，而一般在隔震结构设计中认为支座的拉伸刚度是一个定值，为使简便计算的拉伸变形结果与真实值更接近，支座的拉应力可以控制在零剪应变条件下支座屈服拉应力的二分之一以内，使拉应力在屈服点之前，因此支座在发生水平变形时的拉伸变形不会超过在零剪应变条件下支座的屈服拉伸变形。由于隔震支座的应力-应变曲线在屈服点前是近似线性变化的，因此在零剪应变条件下隔震支座的拉应变限值可以按照建筑抗倾覆要求与建筑性能要求进行确定，并对拉应力限值进行折减，以此确定支座的拉应力设计值，即：

(3)

式中，σd为隔震支座设计拉应力；σy为隔震支座屈服拉应力；ε为隔震支座设计拉应变的最大限值；εyk为隔震支座的屈服拉应变。

2 隔震支座的拉伸性能试验

2.1 试验模型

本次试验采用的隔震支座为B类橡胶制成的Ⅱ型环形隔震支座，支座制作由钢板与橡胶粘结硫化制成，通过添加炭黑、增强剂、促进剂等提高橡胶的力学性能。支座的相关参数及性能均满足《橡胶支座第3部分：建筑隔震橡胶支座》(GB 20688.3—2006)[18]要求，为保证支座的耐久性，在支座外侧设置厚度为10 mm的保护层。将支座置于试验环境中一段时间后进行试验。支座的参数如表1所示。由于经费有限，仅进行了1个改性橡胶隔震支座的拉伸性能试验。

表1 隔震支座参数

2.2 试验装置

进行拉伸试验采用的拉力试验机如图6所示。该试验机采用电液伺服加载，竖向加载量程可达3 500 kN，行程为1 200 mm，采用4个位移传感器进行测量，能精确的测出试验机施加拉力值与支座的拉伸变形量。

图6 隔震支座拉伸装置

2.3 试验内容

在零剪应变条件下，采用1 mm/s的加载速率对支座进行拉伸，拉伸至破坏为止。支座发生破坏的状况如图7和图8所示，破坏面产生许多空洞，橡胶粘结处与支座钢板粘结处均未发生粘结失效破坏。

图7 支座破坏面

图8 支座破坏

3 试验结果及数据处理

改性橡胶支座在受拉状态下，位移-拉力曲线如图9所示，应变-应力如图10所示。屈服应力按相关规范[16]进行确定。

图9 位移-拉力曲线

图10 应变-应力曲线

根据隔震支座的拉伸性能试验结果，隔震支座的拉伸变形过程可分为3个阶段：①未达到屈服点前，处于弹性拉伸阶段，在隔震支座的拉伸过程中，由于此时支座的竖向刚度较大，拉伸变形位移随拉力增大而缓慢增大，随着拉伸不断进行，隔震支座的刚度呈逐渐下降趋势，支座处于弹性拉伸状态。②达到屈服点后，未达到极限点前，处于非弹性拉伸阶段，当支座的受拉变形量达到橡胶总厚度13%，拉力-位移曲线斜率出现下降，即支座的刚度突然降低，造成支座竖向刚度降低的原因可能是因为支座中橡胶内部因拉伸受损产生空洞，从而影响隔震支座性能。此时拉伸变形位移随拉力增大而快速增大，增大趋势近似于平直线，支座仅受到较小的拉力就会使支座产生较大的竖向变形。③达到极限点时，支座发生拉伸破坏，支座在发生破坏前没有明显征兆，当拉应力达到极限点时，支座会突然发生破坏，此时破坏发生在隔震支座中橡胶部分。

根据隔震支座的拉伸性能试验结果可知，该种改性橡胶隔震支座屈服拉应力与极限拉应力很接近，但从屈服点到达极限点的拉伸位移却很大，根据式(5)隔震支座的设计拉应力计算公式，可以确定改性橡胶隔震支座的拉应力设计值为1.855 MPa，此时的拉应力设计值在屈服拉应力之前，可以保证支座在发生较大的变形时，仍有较高的拉伸刚度，同时该改性橡胶支座的拉应力设计值对应的应变为2.5%，与日本规范提出的采用支座拉应变的3%来控制拉应力及刘文光建议的支座拉应变不宜超过10%相近似，支座在受到拉变形时仍能保证建筑的安全。

4 结论

高层建筑采用隔震技术时，由于地震作用影响造成倾覆效应较大，隔震支座容易受拉而影响隔震支座性能，不能保障高层建筑在地震作用中的安全。为解决隔震支座抗拉的问题，本文阐述了新型改性橡胶支座的应用可行性，进行了新型改性橡胶支座的拉伸性能试验，具体结论如下：

(1)根据隔震支座的拉伸试验结果及国内外支座竖向拉伸性能的研究成果，建议将隔震支座的设计拉应力控制在支座的屈服拉应力之前，可以减小支座拉伸变形对支座力学性能的影响。

(2)对隔震支座的拉应力设计值确定方法进行了分析。在参考了各国相关规范、相关的拉伸性能试验和竖向刚度的相关推导理论后，总结了隔震支座的拉应力设计值算法。

(3)通过新型改性橡胶支座的拉伸性能试验，新型改性橡胶隔震支座的屈服应力与极限应力较为接近，测定了新型改性橡胶支座的拉应力设计值为1.855 MPa，对比一般橡胶隔震支座的拉应力不超过1 MPa的要求，新型改性橡胶支座的抗拉性能有所提高，但由于橡胶的物理性能与温度、加载频率等有关，相关因素对隔震支座抗拉性能的影响还有待研究。