基于指数剪切变形理论的层合板湿热分析

胡德义，贺 丹

(沈阳航空航天大学 辽宁省飞行器复合材料结构分析与仿真重点实验室，沈阳 110136)

随着纤维复合材料在湿热环境中的广泛应用，准确预测其在湿热载荷作用下的力学响应变得愈加重要。Lee等[1]基于Kirchhoff经典层合板理论(CPT)研究了在不同边界条件下，湿热效应对横向载荷作用下层合板弯曲的影响。CPT的缺点在于忽略了横向剪切变形的影响，因此不能反映出湿热载荷引起的横向剪切应力，而横向剪切应力恰恰是造成复合材料层合板分层破坏的主要原因之一。Reddy和Hsu[2]基于Mindlin[3]的一阶剪切变形理论(FSDT)，并采用了一种新型有限单元，对复合材料层合板进行热分析。Sai Ram和Sinha[4,5]采用二次等参板弯曲单元，并结合FSDT研究了湿热对层合板弯曲和自由振动行为的影响。FSDT虽然能计算横向剪切应力，但精度不高，且需要引入一个横向剪切修正因子。为了克服FSDT的缺点，人们开始研究高阶理论并对层合板进行湿热分析。Reddy[6]提出了一种著名的三阶剪切变形理论(TSDT)，其位移为厚度方向坐标的三次函数，可自然满足自由表面条件，且不需要引入剪切修正因子，他们将这种理论运用于复合材料层合板的机械/热分析，预测结果与精确解吻合良好。Khdeir和Reddy[7]采用了精细板理论对正角铺设层合板进行了热分析。Savoia和Reddy[8]为简支各向异性层合板的热应力提供了一种三维弹性解。Ali，Bhaskar和Varadan[9]提出了一种位移场中包含一个zigzag函数项的高阶理论，并对对称层合板进行了热分析。展全伟等[10]对湿热环境下开孔复合材料层合板的力学性能进行了试验测定，其结果表明，湿热会降低压缩强度、刚度等材料性能。刘述伦等[11]基于细观力学理论对湿热环境下的纤维增强复合材料层合板进行了屈曲分析。吴振等[12]基于高阶整体-局部理论对湿热载荷下复合材料层合板进行了力学性能分析，并考虑了横向剪切力连续条件和横法向正应变，给出了更为准确的横向剪切应力。

Karama，Afaq和Mistou[13]提出了一种新颖的指数剪切变形理论(ESDT)，其位移模型中除线性项外，还包含了一个指数项，但未知变量的个数与FSDT相同。他们的研究结果表明，ESDT所预测的挠度和应力结果都与精确解吻合良好。然而，他们的研究工作还没有推广到湿热耦合作用的复杂情况。本文的主要目的是基于ESDT理论给出一种模型来准确的预测层合板在湿热载荷耦合作用下的位移和应力响应。

1 指数剪切变形理论

考虑一个如图1所示的N层矩形层合板，长为a，宽为b，厚度为h。中平面定义为z=0，上下表面分别为z=±h/2。

层合板某一点(x,y,z)处的位移场可以表示为

(1)

其中，u,v,w分别为沿x轴、y轴和z轴的位移，u0,v0,w0为中面处位移。u0,v0,w0,φ,ψ都是关于x和y的函数。‘,x’和‘,y’分别表示对x和y求偏导数。F(z)是关于z的指数函数，F(z)=ze-2(z/h)2。由式(1)可得到应变分量为

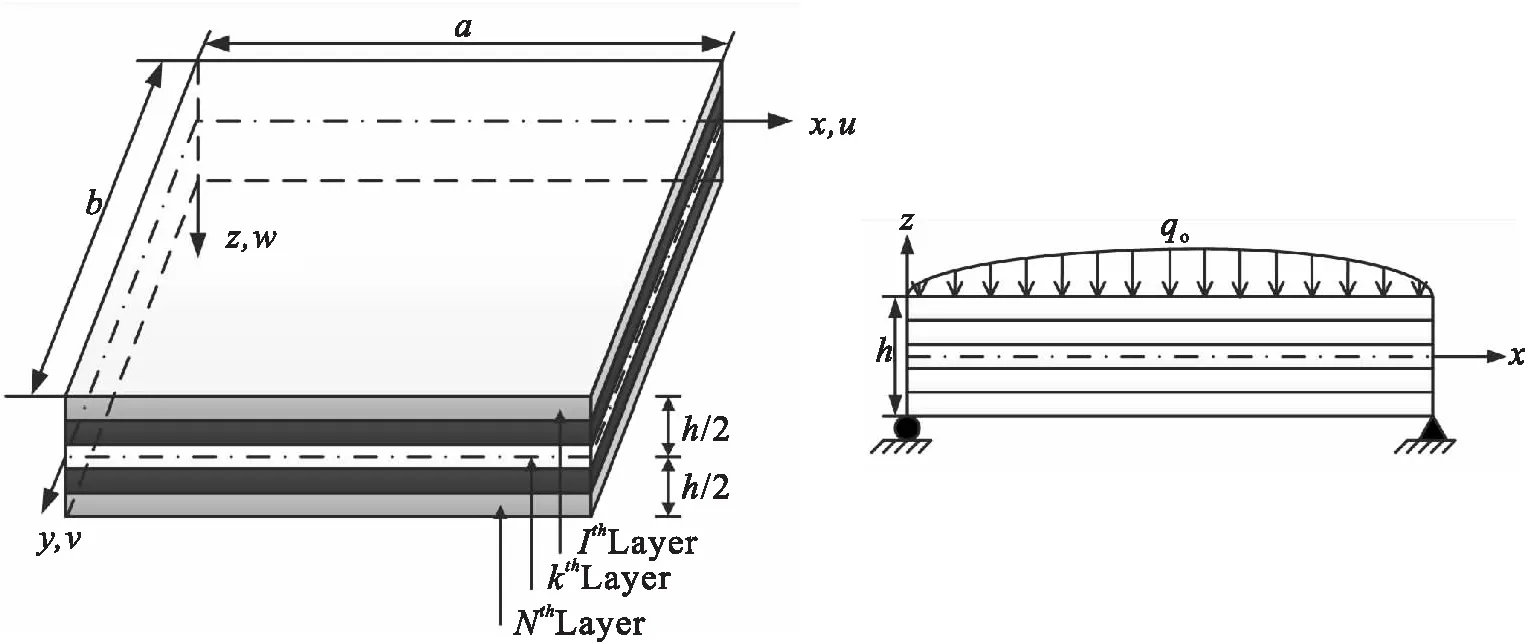
图1 交叉层合板的几何尺寸、坐标系和外载荷

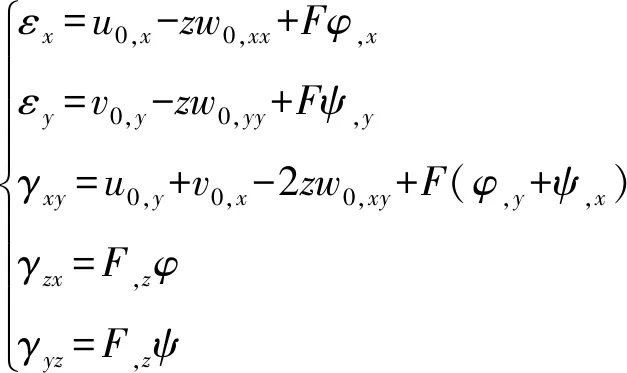
(2)

层合板中第k层的本构关系可以写成

(3)

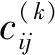
(4)

其中，c=cosθk，s=sinθk，θk为铺层角度，Qij为层合板的材料刚度，即

(5)

其中，Δ=1-vxyvyx-vyzvzy-vxzvzx-2vyxvzyvxz，Ei为材料的弹性模量，vij为泊松比，Gij为剪切模量，此处i、j表示按x、y、z轮换。

通过对式(3)在厚度上积分，可以得到层合板的内力和内力矩

(6)

2 平衡方程和边界条件

由虚功原理可得

(7)

对式(7)进行分部积分，并令δu、δv、δw、δφ和δψ的系数为零，可以得到以内力表示的平衡方程为

(8)

对应的边界条件为

(9)

平衡方程亦可用未知变量u0，v0，w0，φ和ψ重新表示为

δu0:

(10)

δv0:

(11)

δw0:

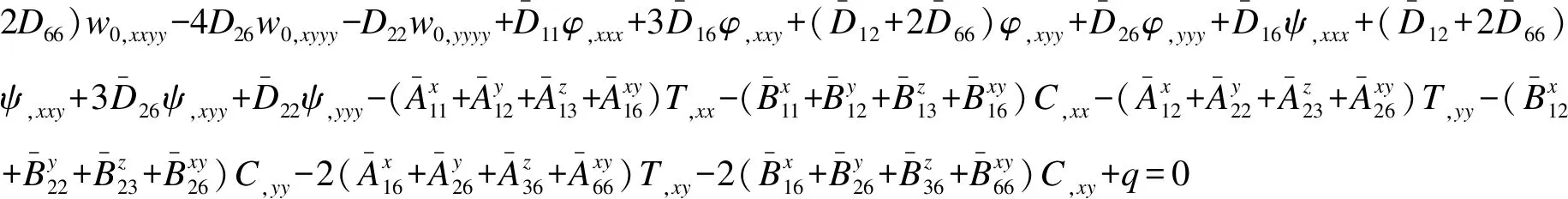
(12)

δφ:

(13)

δψ:

(14)

式中

(15)

(16)

3 算例分析

3.1 四边简支正交铺设层合板的求解

考虑一个如图1所示的受湿热载荷作用的正交铺设的(0°/90°/0°)三层板，各单层的厚度与材料均相同。其几何参数为a/h=10，a/b=1；边界条件为四边简支

atx=0，x=a:v0=w=ψ=ω=Nx=Mx=Sx=0

aty=0，y=b:u0=w=φ=ω=Ny=My=Sy=0

(17)

层合板所受的温度场和湿度场为

(18)

其中，下标1、2和3分别表示与x、y和z方向相关的属性。

横向机械载荷q、温度载荷Tm和湿度载荷Cm分别为

(19)

(20)

此外，对于正交铺设层合板，有αxy=0，βxy=0。

满足边界条件的位移试函数可取为

(21)

式(21)中，Uij，Vij，Wij，Φij和Ψij为待定参数。将式(15)～(21)代入式(10)～(14)中，得到如下矩阵方程

[K]{Δ}={f}

(22)

其中，刚度矩阵[K]的元素为

K11=-(A11α2+A66β2),K12=-(A12+A66)αβ,K13=B11α3+(B12+2B66)aβ2,

(23)

位移向量为

{Δ}={Uij,Vij,Wij,Φij,Ψij}T

(24)

载荷向量{f}的元素为

(25)

根据方程(22)，可求出未知系数Uij，Vij，Wij，Φij和Ψij。将这些系数代入式(21)中，得到相应的位移和应力。横向剪切应力通过三维平衡方程来计算，因此可自然满足层间的剪应力连续条件。

(26)

3.2 结果分析

首先通过与三维弹性解进行比较，证明了在热载荷单独作用时，本文模型给出的位移和应力解具有良好的精度；然后研究了湿、热载荷共同作用时层合板的位移和应力响应，并与文献中的结果进行了对比。

层合板的材料参数取为

(27)

为了便于比较，对结果进行如下无量纲处理

(28)

表1给出了不同理论给出的层合板受载时

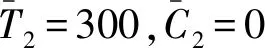
表2中的所有结果是根据理论计算所得，其显示了热和湿热条件下正应力和剪切应力在不同a/h下的值，从表2中数据可以看出，本文模型预测的应力值与精确解吻合良好。FSDT低估了面内应力值；CPT则因为完全忽略了横向剪切变形，导致应力计算结果的误差更大。从结果也可以看出，湿载荷对应力的影响也非常明显。

表2 湿、热载荷共同作用时层合板的应力

图2为热载荷和湿、热载荷作用两种情况下，挠度w随边厚比(a/h)的变化。从图2可以看出，当边厚比小于50时，CPT的误差就开始变得明显。FSDT的精度虽然好于CPT，但其总是倾向于低估板的挠度。另外，还可以看出湿载荷明显增大了板的挠度。随着a/h值得增大，不同理论的预测值趋于一致。

图3a和图3b分别为热载荷和湿、热载荷作用两种情况下，面内位移u沿厚度z方向的变化。几种理论的预测结果基本一致，且湿载荷明显增大了面内位移。

图2 挠度w随边厚比(a/h)的变化

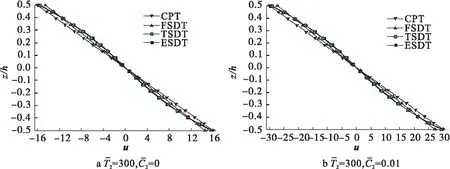
图3 面内位移u沿厚度z方向的分布

图4和图5给出了热载荷和湿、热载荷作用两种情况下正应力σx和σy沿厚度方向的变化图。其中CPT对σy的预测结果与其他几种理论的预测相差较大，且湿载荷明显增大了正应力。

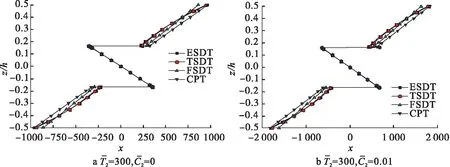
图4 正应力σx沿厚度方向的分布

图6给出了面内剪切应力τxy在厚度上的分布情况，可以看出各种理论的预测结果是基本一致的，且湿载荷明显增大了面内剪切应力。

图7和图8给横向剪切应力τzx和τyz在z方向上的分布。其中，层间界面的横向剪应力均为利用三维平衡方程求得，因此自然满足层间界面的连续条件。从图中可以看出，本文模型和TSDT的预测结果比较接近，CPT的预测结果偏大。另外，湿载荷明显增大了横向剪切应力。

图5 正应力σy沿厚度的分布

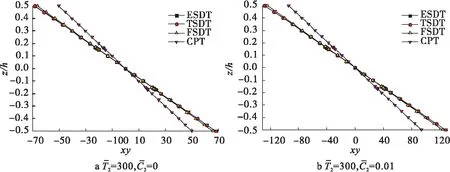
图6 面内剪切应力τxy在厚度上的分布

图7 横向剪切应力τzx沿厚度的分布

图8 横向剪切应力τyz沿厚度的分布

4 结论

本文基于指数剪切变形理论建立了机械、湿、热载荷耦合作用的层合板静力分析模型，并以正交铺设层合板为例进行了计算和分析，结论如下：

(1)对于热载荷单独作用的情况，本文模型能够较为精确的预测位移和应力响应，尤其与经典层合板理论及一阶剪切变形理论相比优势明显。

(2)当湿、热载荷共同作用时，本文模型所预测出的挠度、面内应力及横向剪切应力都比经典理论或一阶剪切变形理论精确的多。但本文模型的解与三阶剪切变形理论相比是非常接近的，因此可作为三阶剪切理论的一种替代。

(3)湿载荷会显著的增加结构的挠度和应力水平，因此在实际应用中要特别加以注意。

(4)为了便于与文献结果进行对比，本文算例中未考虑机械载荷作用。然而，该模型是通用的，可适用于机械、热和湿载荷共同作用的情况。