超声速气液两相清洗喷头计算
2021-01-27田骏丹徐让书刘宗旺
田骏丹,徐让书,刘宗旺
(沈阳航空航天大学 航空发动机学院,沈阳 110136)
超声速气液两相清洗喷头利用空气与液相颗粒混合,经过Laval喷管形成超声速气液两相流来清洗机械零部件的内腔表面。清洗喷头的射流压力、流量等影响清洗效果和清洗效率。两相质量流量对两相流动速度特性影响显著,相同质量流量情况下,液相颗粒越多,颗粒直径越小,气相出口马赫数越小[1,2]。Chang I.S用双流体模型研究了液相颗粒直径和流量对两相流的影响,结果表明小直径颗粒能有效减缓气相膨胀,且液相颗粒流量较大的情况下,喷管喉部可处于亚声速状态[3];两相流中的液相颗粒由喷管进口端的水喷嘴产生,液相颗粒直径随水喷嘴射流速度增大而减小、随流量减小而减小[4];水喷嘴出口液相颗粒按照Rosin-Rammler函数分布[5,6]。针对某确定型线的超声速气液两相清洗喷头中有摩擦和添质的广义准一维稀颗粒群两相流,进行了数值计算与分析,找出该喷头工作压力与液相流量的控制规律,确定液相颗粒进口温度范围。
1 超声速气液两相流动计算
超声速气液两相清洗喷头的核心气动结构为Laval喷管。喷管型线的收缩段和扩散段分别采用Вцмощцискцǔ公式[7]和4次多项式拟合,两段长度均为0.02 m。水喷嘴布置在Laval喷管进口端,其轴线与喷管轴线垂直,喷头工作时,根据实际情况选择4个水喷嘴中的一个。喷头结构以及实物如图1所示。

图1 超声速气液两相清洗喷头
1.1 计算模型
喷管中是有摩擦和添质的广义准一维稀颗粒群两相流亚声速-超声速流动。根据流动性质建立物理模型有以下假设:
(1)假设喷管任意截面上的流动参数是均匀的,是关于喷管轴向距离x的函数,即喷管中的流动为准一维流动;
(2)喷管尺寸小,两相流速大,流体与喷管壁面的接触面积小、热交换时间短,假设喷管壁绝热;
(3)雾化的液相颗粒在喷管中连续分布,形状为球形,流动过程中不发生破碎和相变,假设液相为拟流体[8]。
根据物理模型,推导守恒型两相流动的质量守恒、能量守恒和动量守恒方程组,并对其进行无量纲化处理。
(1)
(2)
(3)
(4)
(5)
(6)
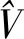
为方便编写差分程序求解,将控制方程组(1)~(6)写作通用形式如式(7)、式(8)所示
(7)
(8)
式(7)、(8)中U、F、J分别为解变量、通量和源项。k=1,2,3时,分别代表质量守恒、动量守恒和能量守恒方程组。
1.2 边界条件
Laval喷管进口为亚声速,左行特征线离开计算域,右行特征线和流线进入计算域,需设定总密度和总能不变[10]。气相和液相颗粒的速度采用两相平衡流条件和特征线法确定。液相颗粒的尺寸是采用简单孔式喷嘴参数化模型计算的最可几直径d0=42 μm。入口气相温度和液相颗粒温度给定。
Laval喷管出口边界气相为超声速流(液相颗粒不定),流线和两条特征线离开计算域,流动参数不固定。
Laval喷管壁面对于气液两相皆为绝热,管壁对气液两相的加热率δQ为0。
1.3 数值计算方法
用MacCormack显式有限差分方法[11,12]时间推进求解两相流控制方程组。对于中间节点,该方法使用两次预估—校正过程,预估步中用向前差分代替空间导数,取泰勒级数的前两项作为待求参量当前时刻(t时刻)的估计值。校正步中先用向后差分代替空间导数,用参量的预估值计算时间导数在下一时刻(t+Δt时刻)的预估值,然后取当前时刻时间导数预估值与下一时刻时间预估值的算数平均,最后用平均时间导数求解下一时刻的参量值。
对于进口边界节点,由特征线理论[13-14]先给出气相速度,由气相速度可得出其他参数。由一维不定常两相流的左行特征线方程及其相容性方程,结合等熵关系式与平衡两相流条件给出入口气相速度表达式,再由气相速度得出气相温度、压力和密度的表达式,由两相平衡流条件得液相颗粒的速度和温度。两相解变量、通量与源项由两相流动参数直接表达。
对于出口边界节点,由于流动参数均不固定,气液两相的解变量、通量与源项由内部节点外插值计算,然后反向计算出口节点的两相流动参数。
2 计算结果与分析
本文计算了某超声速清洗喷头喷管的广义准一维稀颗粒群两相流亚声速-超声速流动,研究不同进口总压、进口液相温度、液相流量和液相颗粒直径对喷管出口速度、动量和能量的影响规律,针对该超声速气液两相喷头的工况,找到其工作参数范围,以对相关喷射设备的设计计算提供理论参考。
2.1 喷管中两相流动参数
图2是喷管在设计工况压比18.25时的气相和液相颗粒速度沿轴向的分布,气相速度在出口达到马赫2以上;图2中同时给出了喷管型线y(x)。该工况喷管出口为大气压,液相流量为0.025 kg/s,液相颗粒直径为42 μm,该直径是在水喷嘴设计参数下雾化的最可几直径。
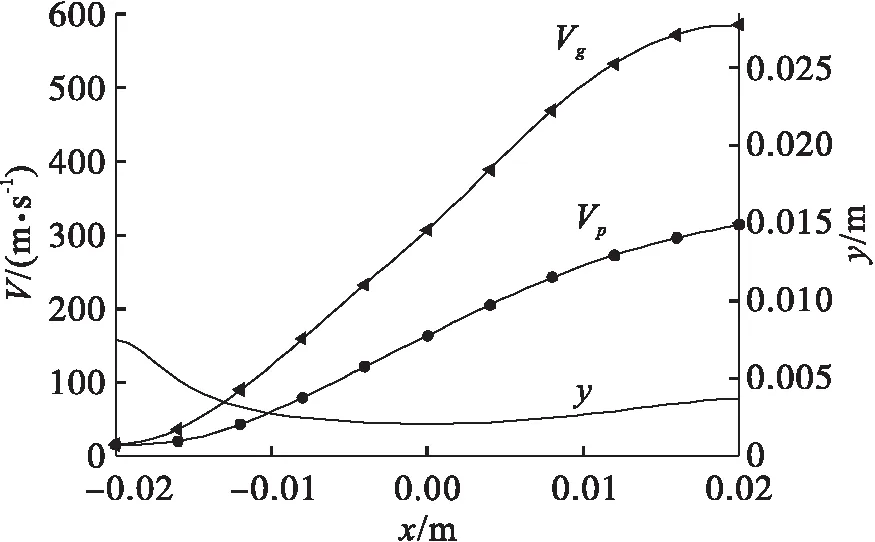
图2 气相和液相颗粒速度沿轴向的分布
图3是喷管在设计工况压比18.25时温度和压力沿轴向的分布。液相颗粒从喷管入口到出口,其温度仅降低4.4 K,而气相温度降低198 K。两相作用导致压力在喷管进口附近略有上升,然后逐渐降低至喷管出口为0.104 MPa。

图3 喷管中温度和压力沿轴向的分布
2.2 出口速度及颗粒动量与能量
喷管出口气相和液相的速度以及颗粒的动量与能量等参数影响清洗效果。颗粒的动量与能量越大清洗效果越好,同时对被清洗表面损伤越大,实际运用中应根据被清洗零部件的表面情况合理控制。
图4为在不同液相流量和入口压力下,液相颗粒直径对出口气相速度和液相颗粒速度的影响。颗粒直径dp主要是通过动量传递弛豫时间τv影响两相之间的动量交换。在液相流量和入口总压一定时,随着颗粒直径增大,颗粒数减少且τv增大,使两相之间的动量交换减弱,减慢了颗粒在喷管中的加速过程,因此液相颗粒出口速度降低;同时气相的动量损失较少,因此气相出口马赫数随着dp增大而提高。
在液相流量和颗粒直径一定的情况下,喷管入口总压提高,进而通过增大气相密度以及颗粒雷诺数而减小颗粒的τv,增强两相间的动量交换,使颗粒具有更好的跟随性,因此液相颗粒的出口速度增加;而在入口密度更大的情况下,气相的动量流量率也更高,因此尽管气相将更多动量传递给液相颗粒,气相的出口马赫数仍然是增加的。
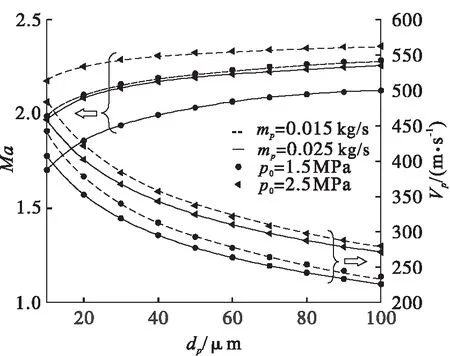
图4 液相颗粒直径对两相出口速度的影响
图5是在不同液相流量和入口压力下,在喷管出口单个液相颗粒的动量、能量与直径的关系。出口颗粒能量和动量越大,被清洗表面的冲刷作用越大,对清洗表面的损伤也越大。
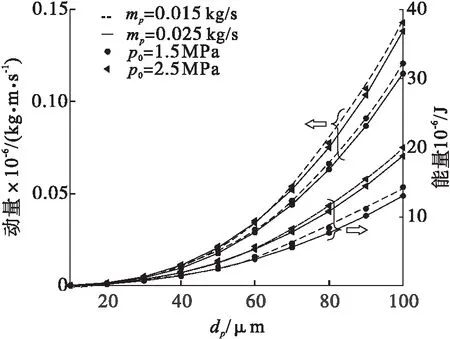
图5 单个颗粒的出口动量和能量与直径的关系
增加液相流量和降低入口总压使喷管出口的气相马赫数减小和液相颗粒速度小幅度降低。因此,该清洗喷头在使用过程中应根据被清洗表面的污染情况,控制液相清洁剂的流量以达到最佳清洗效果。
2.3 喷管入口压力及温度控制规律
清洗喷头要求喷管在设计工况,即出口截面压力等于背压的情况下工作。如果偏离设计工况,喷管出口将形成激波或膨胀波,造成射流中速度方向偏转并产生强烈噪声[15]。而液相流量影响喷管设计工况的压比,因此需要找到在给定背压时喷管入口压力随着液相流量的变化关系,作为控制规律。为此,计算了不同进口总压p0和液相流量mp时的出口马赫数和出口压力,其变化规律如图6所示。在进口总压一定时,随着液相流量的增加,出口马赫数下降,同时出口截面的压力上升。
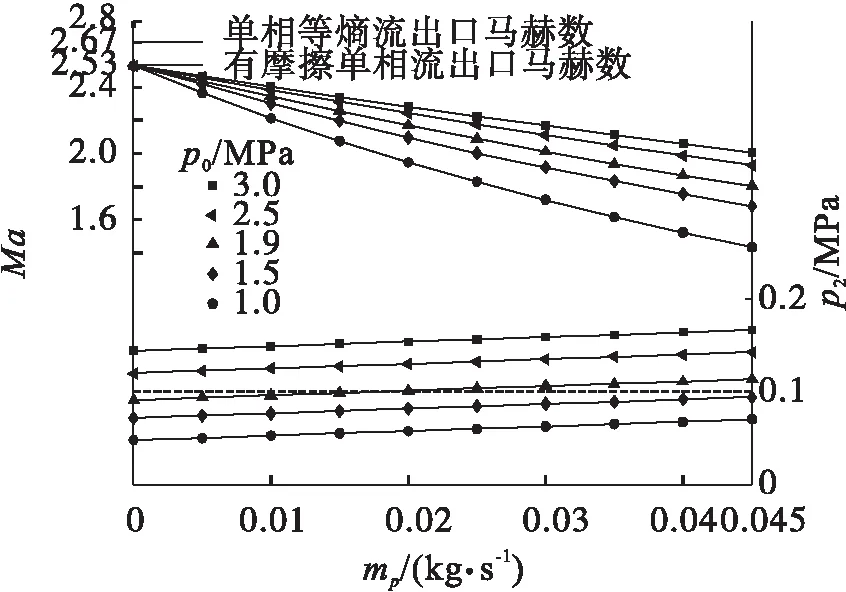
图6 气相出口马赫数与入口总压和液相流量的关系
在大气中工作的喷头其出口压力应等于大气压。采用插值方法,计算出口压力为标准大气压时不同液相流量所对应的进口总压,入口压力以及对应的马赫数随液相流量的变化关系如图7所示。为了使喷管在设计工况下工作,不同液相流量时的入口总压应按该曲线确定。
如果液滴进口温度过高,在喷管出口附近会发生沸腾,从而严重影响清洗性能。
图8是进口气相温度为120 ℃,且进口总压按图7的规律变化时,在不同颗粒进口温度的条件下,液相颗粒出口温度与液相流量的变化关系。当入口颗粒温度不超过103 ℃、出口颗粒温度不超过100 ℃时,从喷管入口到出口运动过程中,颗粒温度低于当地压力下水的饱和温度,不会发生沸腾。

图7 出口压力为标准大气压时喷管设计工况入口总压与液相流量的关系
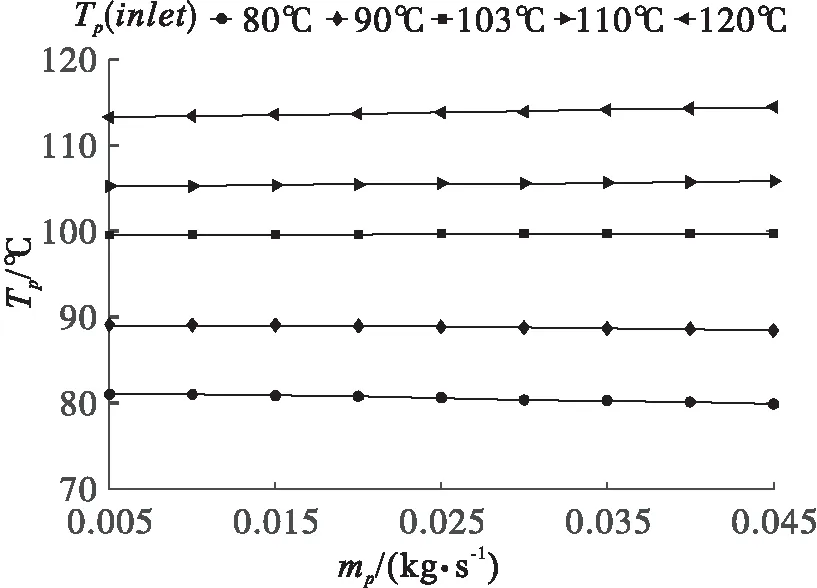
图8 出口颗粒相温度与液相流量的关系
3 结论
本文基于有摩擦和添质的广义准一维稀颗粒群两相流亚声速-超声速流动模型,对超声速两相清洗喷头Laval喷管中的流动参数进行数值求解,得到以下结论:
(1)在设计马赫数为2的长度40 mm的超声速两相清洗喷头缩放喷管中,出口处最可几直径水雾颗粒的速度可以达到气相速度50%以上。
(2)随着颗粒直径增大,喷管出口液相颗粒速度降低,而单个颗粒的动量和能量增加;提高入口总压或减小液相流量,出口处液相颗粒速度以及单个颗粒的动量和能量均增加,且出口马赫数增大。
(3)为了使清洗喷头的喷管工作在设计工况,应按出口压力等于背压的条件所确定的规律调节入口总压。随着液相流量的增加,该设计工况总压值几乎是按线性的关系降低的,同时出口马赫数也减小。
(4)为避免液相颗粒发生沸腾,当进口气相温度为120 ℃时,液相颗粒的入口温度不应超过103 ℃。
