高空台动静架新型非接触密封结构设计

2021-01-27王志李吉凯苏金友赵丹杨志明张凤玲

沈阳航空航天大学学报 2020年6期

王志，李吉凯，苏金友，赵丹，杨志明，张凤玲

(1.沈阳航空航天大学辽宁省航空推进系统先进测试技术重点实验室,沈阳 110136；2.中国航发四川燃气涡轮研究院高空模拟技术国防重点实验室，绵阳 621000 )

在进行航空发动机高空飞行模拟试验时，发动机安装于推力测试平台动架上，动架与静架间一般采用非接触的蓖齿封严结构连接。由于篦齿连接结构本身预留较大间隙，因此导致蓖齿封严结构泄漏量较大，需要额外进行气体补充，才能提高高空台对发动机推力测量的精准度。在研究非接触密封结构参数对密封结构泄漏量影响方面，巴鹏等[1]应用动网格技术对迷宫密封的齿形进行了相关的研究，研究表明当其他条件相同时，矩形齿的密封效果最好；吴丁毅[2]在直通式蓖齿密封中研究了密封齿尖厚度与间隙比，齿数以及气流方向对结构封严性能的影响，得知密封性能受到间隙影响较大，密封齿数超过8个时，再增加齿数对于密封性能几乎没有影响的规律；丁学俊等[3]应用Fluent软件计算迷宫密封斜齿角度和三角齿型对泄漏量的影响，发现当倾斜角度增加时，泄漏量由大到小再到大；随着三角齿根角度的增加,泄漏量也由大到小再到大；巴鹏等[4]建立三维迷宫模型，研究密封间隙对密封性能的影响，发现随着间隙宽度的增大，流体速度降低，迷宫间隙内的节流效应降低，泄漏量逐渐增大；李钰洁等[5]研究涡轮叶顶密封时发现随着密封间隙的增大，密封结构的泄露量也随之增大。

针对现有高空台动静架连接的金属篦齿密封间隙预留过大问题，本文提出采用聚四氟乙烯(PTFE)作非接触密封圈的新型密封结构来替换蓖齿封严结构。聚四氟乙烯(PTFE)被称为“塑料之王”，作为动静架的密封材料(密封圈)，与传统的橡胶材质密封圈相比，其优点是具有较大的弹性模量，受大的应力作用不会因发生较大形变而导致密封间隙变大，进而导致密封失效。该材料本身又具有极低的摩擦系数，因此既可以作为接触密封材料，也可以作为非接触密封材料，本文将其作为非接触密封材料使用。

目前大多数学者所研究的是聚四氟乙烯材料及其复合材料的摩擦特性，如叶素娟等[6]对不同PTFE复合材料密封圈摩擦特性进行了对比研究，发现填充其他材料后能显著提高聚四氟乙烯的抗磨性能；Tzanakis等[7]将PTFE复合材料用在高碳钢上进行摩擦特性分析，与其他材料相比，含Cr2O3的青铜( PTFE )复合材料具有优异的抗磨损性能[8]。国外还有学者研究在摩擦热的影响下，PTFE复合材料的压缩蠕变对于密封配合间隙的影响[9]，上述学者主要研究的是PTFE用于接触式工作环境下的性质，而对于PTFE用于非接触密封的研究较少。祝娟等[10]对变截面密封圈几何参数对密封性能的影响进行了研究，分析了截面几何参数对密封圈应力分布的影响。

关于CFX仿真计算方面，多数学者[11-13]应用CFX计算研究结构参数和工况对流场模型的压力分布、速度分布和温度分布规律，进而指导结构优化设计。范晋伟[14]通过应用CFX研究液压轴承的关键结构参数对其油膜压力分布的影响，并用于指导液压轴承的优化设计；崔亚辉[15]应用CFX研究密封间隙和预旋角度对迷宫密封泄漏量和动特性系数的影响规律。

关于泄漏量的相关计算，国外学者[16-19]给出了一些经验公式，但是由于公式假设条件比较苛刻，不具有通用性，因此本文采用软件自带流量公式来计算所研究模型的泄漏量。

1 模型的建立

1.1 模型尺寸

本文应用PTFE作为密封结构材料来替换动静架连接处的篦齿密封结构，将PTFE密封材料设计为圆环形密封圈。密封圈的横截面初步设计为D形截面和梯形截面两种，密封圈的类型和具体尺寸见图1和图2所示。图中高度h的取值随密封间隙改变，依次为3.5 mm、4 mm、4.5 mm、4.7 mm和4.9 mm。

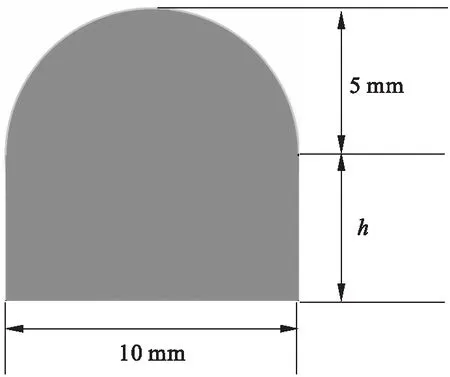
图1 D形密封圈横截面示意图

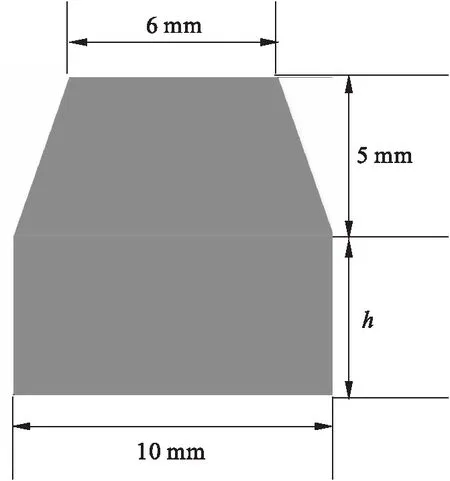
图2 梯形密封圈横截面示意图

以梯形截面形状密封圈模型为例，有限元模型如图3所示，密封圈间用金属圆环分隔固定，同时在密封圈和固定环之间形成腔体，密封圈顶端与筒壁的内壁之间的距离为密封间隙。在保证模型计算结果准确的前提下，为了节省计算时间和降低计算对电脑配置的过高要求，应用实际试验件密封段的1/4建立有限元模型。气流通过进气口导入到密封装置中，当气流进入到腔体时气流会发生膨胀，动能耗散导致气流的动能减少。当气流流经密封间隙时气流会发生节流效应，导致气体压力值降低。当气流每次流经密封装置内的腔体和密封间隙时，气流的动能和压力值会逐渐降低，最终由出气口流出。

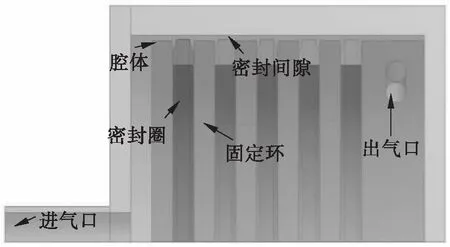
图3 有限元模型

1.2 网格划分

图4为有限元模型的网格划分示意图，进行网格划分时将整个流体域模型分为两部分。整体部分的网格尺寸设置为1 mm，对另外尖端小尺寸的部位进行网格尺寸加密处理，网格尺寸设置为0.5 mm，以此来提高网格质量，提升计算结果的精准度。

图4 有限元模型网格划分

从图5中可以看到，当网格的数量大约为150万时，再增加网格数量对于结果几乎没有影响，泄漏量波动小于0.1%，由此认定此时网格数对计算结果的影响不大。最终所有流体域计算模型的网格数量为140～160万之间。

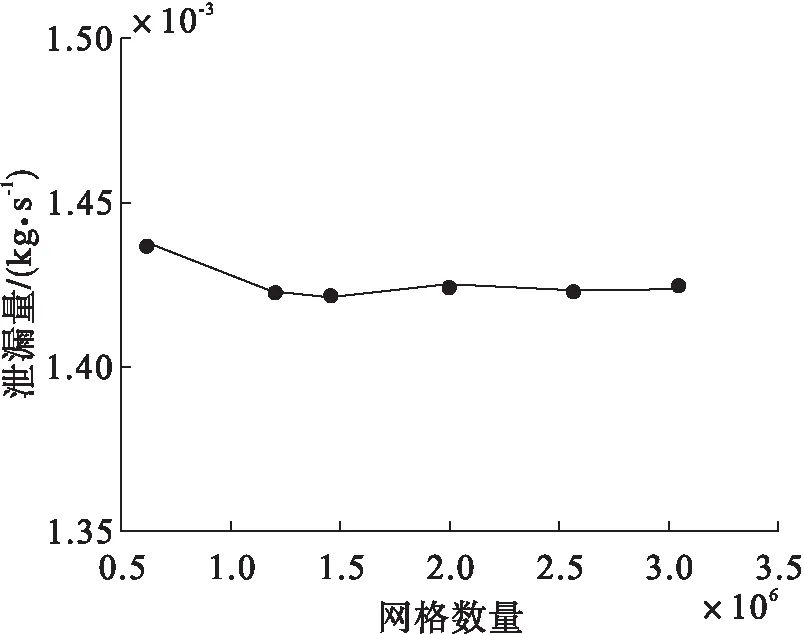
图5 网格无关性检验图

1.3 密封段湍流模型

设工质为可压缩理想气体，黏性系数满足Sutherland假设，数值计算采用时间追赶的有限体积法，求解三维稳态Realizablek-ε方程。收敛判断标准为：连续方程、动量方程和湍流方程的均方根残差下降到10-4～10-5，进出口质量流量差值小于0.01%，认为计算收敛。应用CFX中的自带的流量公式函数来计算泄漏量。Realizablek-ε方程如下

(1)

(2)

式(1)、(2)中,k为湍流动能，ε为湍动耗散率，σk,σε为湍流动能和湍动耗散率对应的Prandtl数，σk=1,σε=1.2；xi,xj为位置坐标分量；μi为速度坐标分量；Gk为平均速度梯度引起的湍流动能k的产生项；μ为流体动力粘性系数。流体动力粘性系数μ=ρCμk2/σε，Cμ为模型常数，C2=1.9。

1.4 边界条件设置

研究密封结构泄漏特性时，入口设置为总压、总温进口。出口给定为压力出口，压力值为标准大气压。表1给出了填充材料密封结构模型的边界条件，其中压力比为进气口与出气口压力之比。

表1 填充材料密封边界条件

2 仿真计算及结果分析

2.1 密封圈横截面形状对新型密封结构泄漏特性的影响

设计优异的横截面形状密封圈不仅可以起到良好的密封效果，同时有利于降低加工生产的难度，对于后期的使用和维护也有很大的便利。本次设计密封圈截面形状初步选定D形截面和梯形截面。以泄漏量为评判依据，通过仿真计算分析，筛选密封性能优异的密封圈进行结构参数对密封特性影响研究。同时，研究当密封圈截面形状相同时密封间隙对密封结构的密封特性影响规律。密封间隙的选取依次为1.5 mm、1 mm、0.5 mm、0.3 mm、0.1 mm。以此来研究当密封间隙改变时，密封结构泄漏量随之变化的规律。

横向比较图6a和图6b，图7a和图7b,同时通过对比表2和表3中的压降值可知，当密封间隙减小时，出口端压力值显著降低，压降值显著提升，密封结构压降效果提升。纵向比较时，同样的密封间隙工况下，梯形截面密封圈的密封特性都要比D形截面密封圈的密封特性更加优异。因此选取梯形截面作为密封圈的横截面形状更具优势。

图6 D形密封圈，压力比2.0，5个密封圈，不同密封间隙压力云图

从表2和表3可以得知，无论是D形截面密封圈还是梯形截面密封圈，当密封间隙减小时密封结构使气体压降值显著增强。密封结构泄漏量显著降低如图8所示。

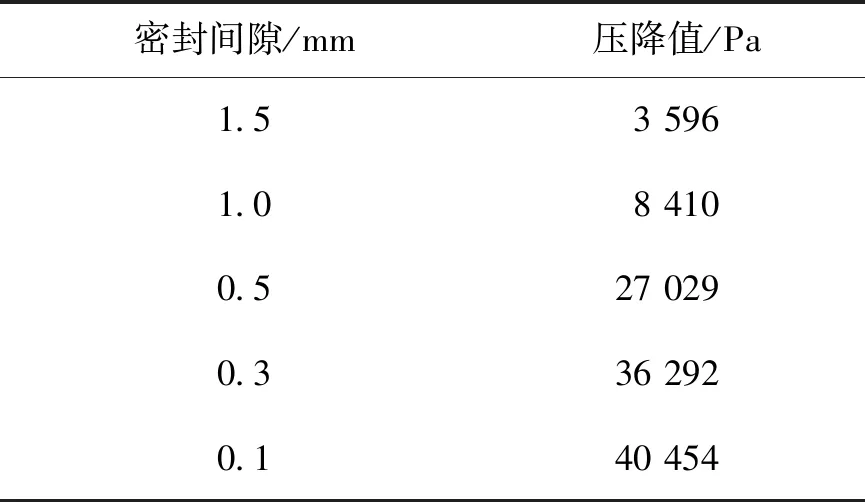
表3 梯形密封圈不同密封间隙压降值

图8 密封间隙及密封圈截面形状对泄漏量影响趋势图

从图8可知，当D形截面密封圈的密封间隙从1.5 mm变成0.1 mm时，密封结构泄漏量降低84.44%。当梯形截面密封圈的密封间隙从1.5 mm变成0.1 mm时，密封结构泄漏量降低91.82%。从图8看出，随着密封间隙的减小，梯形截面密封圈的泄漏量始终低于D形截面密封圈的泄漏量。

2.2 进出口压力比对新型密封结构泄漏特性的影响

由于密封结构工作环境的特殊性，其工作介质为流体，因此密封结构进出口压力比对密封结构设计有着一定的影响作用。采用梯形截面密封圈作为密封结构的密封部件，选取密封圈个数为5，密封间隙为0.1 mm和0.3 mm的密封段模型来研究压力比对于密封结构密封特性的影响规律。出口端连接大气环境，进出口压力比依次设定为1.5、1.8、2.0、2.3、2.5。

从表4可以看出，随着压力比的增加，虽然密封结构的压降值增加，但是此时对压力云图的出口端压力值采样时，发现出口端压力值也在增加，因此导致密封结构泄漏量增加，如图9所示。由此断定出口端压力值也是判断密封结构性能的一个重要指标。因此当用压力值来评价一个密封装置的密封特性时，应关注密封结构压降值和出口端压力值两个参数，来评价密封结构的密封特性的优良。

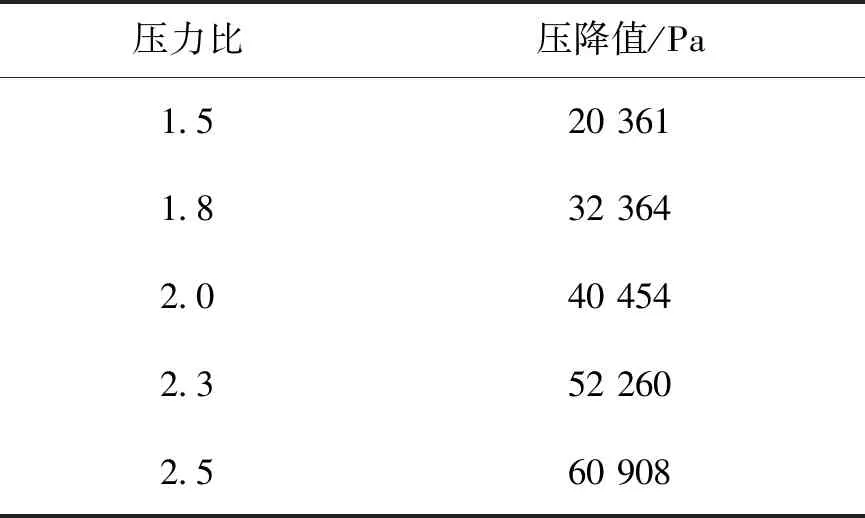
表4 不同压力比下密封结构压降值

从图9得知，当密封间隙为0.1 mm，密封圈个数为5个，压力比从2.5降低至1.5时密封结构泄漏量降低71.43%。当密封间隙为0.3 mm，密封圈个数为5个，压力比从2.5降低至1.5时、密封结构泄漏量降低77.79%。由此得知，进出口压力比对密封结构的密封特性有较大影响。从图9可以看出，在一定条件下密封间隙对结构泄漏量的影响要大于压力比对结构泄漏量的影响。

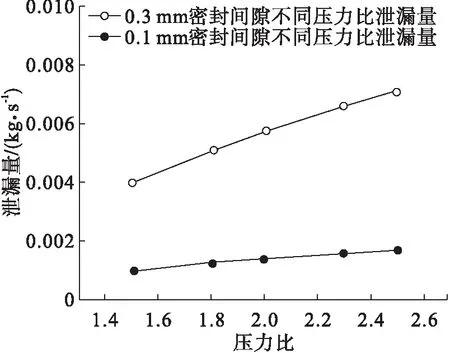
图9 压力比对于泄漏量的影响趋势图

2.3 密封圈个数对新型密封结构泄漏特性的影响

从安装工艺、材料用量与泄漏量平衡的角度出发，设计适当的密封圈个数不仅可以有效降低泄漏量，而且还能降低结构的加工及维护成本。通过仿真计算与分析，研究梯形截面密封圈密封间隙为0.1 mm，压力比为1.5、2.0和2.5时，密封圈个数分别为5、4和3时对密封结构泄漏特性的影响规律。

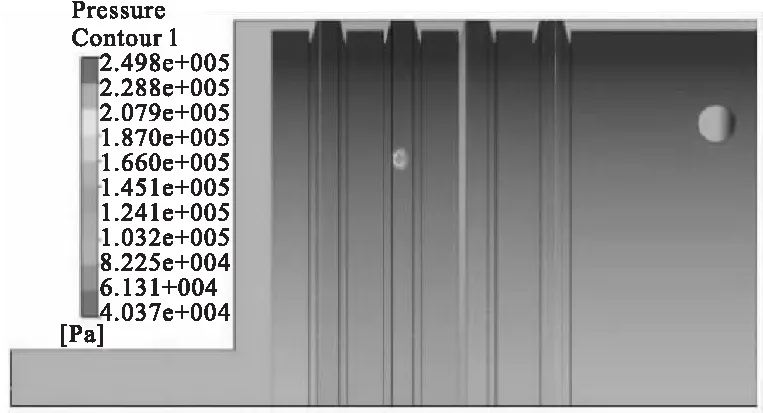
图10 4个密封圈，密封间隙0.1 mm，压力比1.5压力云图

图11 3个密封圈，密封间隙0.1 mm，压力比1.5压力云图

当压力比为1.5，密封间隙为0.1 mm时，密封圈个数由3个增加至5个时，泄漏量降低19.65%；当压力比为2.0，密封间隙为0.1 mm时密封圈个数由3个增加至5个时，泄漏量降低22.42%。当压力比为2.5，密封间隙为0.1 mm时密封圈个数由3个增加至5个时，泄漏量降低22.96%。同时从图12可以看出，在一定条件下压力比对结构泄漏量的影响要大于改变密封圈个数对结构泄漏量的影响。