一类机器人的示教奇异位形预测
2021-01-24徐善军任书楠李聪利
陈 皓,徐善军,任书楠,宁 昕,李聪利
(1.国电富通科技发展有限责任公司,北京 100071;2.国网天津市电力公司,天津 300010)
0 引言
随着科技的发展,机器人的使用范围也日益加大,一些传统、危险的人工操作也逐渐被机器人替代[1]。丹麦机器人制造商Universal Robots公司的协作机器人凭借优异的灵活度、安全性和独特创新的人机协同能力[2],颠覆了传统工业机器人笨重及昂贵的特征[2],可以利用有限的空间和资源实现人机灵活、安全协同作业,因此在现代工业中具有广阔的应用场景[2~5]。然而在实际的运动控制中,由于操作人员缺乏对机器人运动学[2],奇异性的理解[2],经常设置不合理路点[2],使得机器人作业时出现保护性停止、找不到解决方案、机器人不能到达该位置等警报[2],此时操作人员需要手动清除报警信息并重新上电初始化机器人。如此往复增加了调试的难度,也降低了一线操作人员的使用体验度。
本文针对该问题,基于现有UR10机器人本体,考虑了机械臂的可行空间,建立了六轴机器人运动学模型。目前算法对多约束、环境复杂的条件下的奇异点预测不能快速实时找到问题的相关解,本文将寻求其他的算法在该问题上的应用,设计了示教过程中对奇异位形的预测算法,实时计算未来轨迹,避免了现有UR机器人在作业过程中遇到的上述问题。该方法原理具有通用性,可移植性强,成本代价小。
1 运动学分析
机械臂运动学特性的研究主要包括正运动学与逆运动学,正运动学即已知关节空间轴坐标求笛卡尔坐标系下末端位姿,逆运动学即已知机器人末端在笛卡尔坐标系下的位姿,求解关节轴位置[8]。该问题为预测奇异位形的基础。
1.1 连杆参数描述
本文使用的连杆参数描述机构运动关系的规则为Denavit-Hartenberg参数[9],相邻连杆参数由α,a,d,θ构成,关节连杆参数示意图如图1所示。其中,αi表示绕Xi-1,Zi-1到Zi的旋转角度;ai表示沿着Xi-1,Zi-1到Zi的距离;di表示沿着Zi-1,Xi-1到Xi的距离;θi表示绕Zi-1,Xi-1到Xi的旋转角度。

图1 转动关节连杆参数示意图
1.2 坐标系
建立如图2所示机器人坐标系,并根据该坐标系和1.1中的关节连杆参数描述,确定如表1所示的ur10机器人标准DH参数。

图2 UR10机器人坐标系
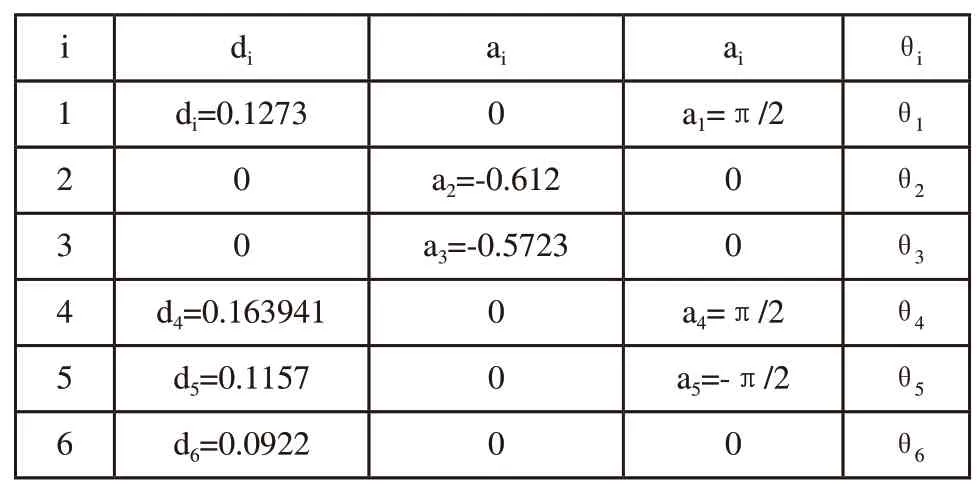
表1 UR10机器人标准D-H参数
1.3 正运动学

1.4 逆运动学
因UR10机器人满足Pieper准则,具有封闭解[11]。相较于数值解,解析解在精度和计算速度上有明显优势,本文设计的一类奇异位形实时预测算法选择了解析法。根据式(2)左右同乘01T-1,右乘56T-1,可得分别展开等式的第3行4列,可得到关于θ1的三角函数方程;展开第3行3列,得到关于θ5的函数方程;展开第3行1列,得到关于θ6的方程。通过该方法用三角函数万能公式先求解θ1,再求解θ5,θ6,再求解θ3,最后求解θ2,θ4,其中令:

2 示教轨迹预测及奇异分析
协作机器人的示教控制方式包括拖拽示教、J1-J6轴动以及机器人末端工具中心位置(TCP)基于笛坐标系的单向移动。其中,基于轴关节空间的拖拽和轴动不会遇到奇异等问题,不在本文考虑范围内。TCP的单向移动根据自由度类型分为位置方向移动和姿态旋转移动;根据参考坐标系分为基坐标系和工具坐标系等。
2.1 位置示教

2.2 姿态示教

2.3 奇异位形及不可达预测分析
奇异位形分为工作空间边界及内部两种,前者使得执行末端接近工作空间边界,后者通常是由于至少两个关节轴发生共线。当机器人处于奇异位形,它会失去一个或多个自由度,此时,无论选择什么样的关节速度都无法使机械臂末端运动;在途经奇异位形时,某些关节轴会尝试瞬间旋转180°,对设备造成损伤。本文利用矢量积法求得雅可比矩阵[12],并令可求得UR机器人在奇异位形状的条件是式中三个因子对应的物理意义分别是四六轴共线、二三四轴共面、末端位置在一二轴构成的平面。实际示教运动中为了提前预知上述位形及不可达位姿,设计了如下算法进行预测。
步骤1:获得当前i时刻六个关节轴位置信息。
步骤2:判断当前是否为奇异点,若是,则结束,预测结果给true;若否,则到步骤3)。
步骤3;正解得i时刻TCP位姿。
步骤4:根据当前命令请求(如基于极坐标系X轴正方向),计算i+1时刻TCP位姿。
步骤5:运动学逆解得i+1关节轴角度。
步骤6:是否存在逆解释,若是,则到步骤7);若否,则结束,路径将不可达,预测结果给true。
步骤7:选择最有效解中最优解。其中有效解表示在轴关节可行范围内,最优解原则即为i时刻
步骤8:判断i,i+1关轴差分是否大于阈值,若是,则结束,预测结果给true;若否,则到步骤9)。
步骤9:判断运动是否结束;若是,则结束,预测结果给false;若否,则i++并到步骤4)。
3 实验设计与验证分析
为了验证运动学算法及奇异位形预测的有效性,本文设计了两个算例,一个算例验证了ur10机器人运动学,另一个算例基于ROS设计了奇异位形预测节点,在真实环境中验证2.3算法在示教过程中对不可达点及奇异形的预测。
3.1 运动学验证

由该末端ΘT逆解出可能对应关节坐标组合值如表2所示。反之,由表2得到的8组解再重新求得8组的末端姿态Ti,此时对比结果,发现由此可以互相验证其运动学的正、逆解的正确性。
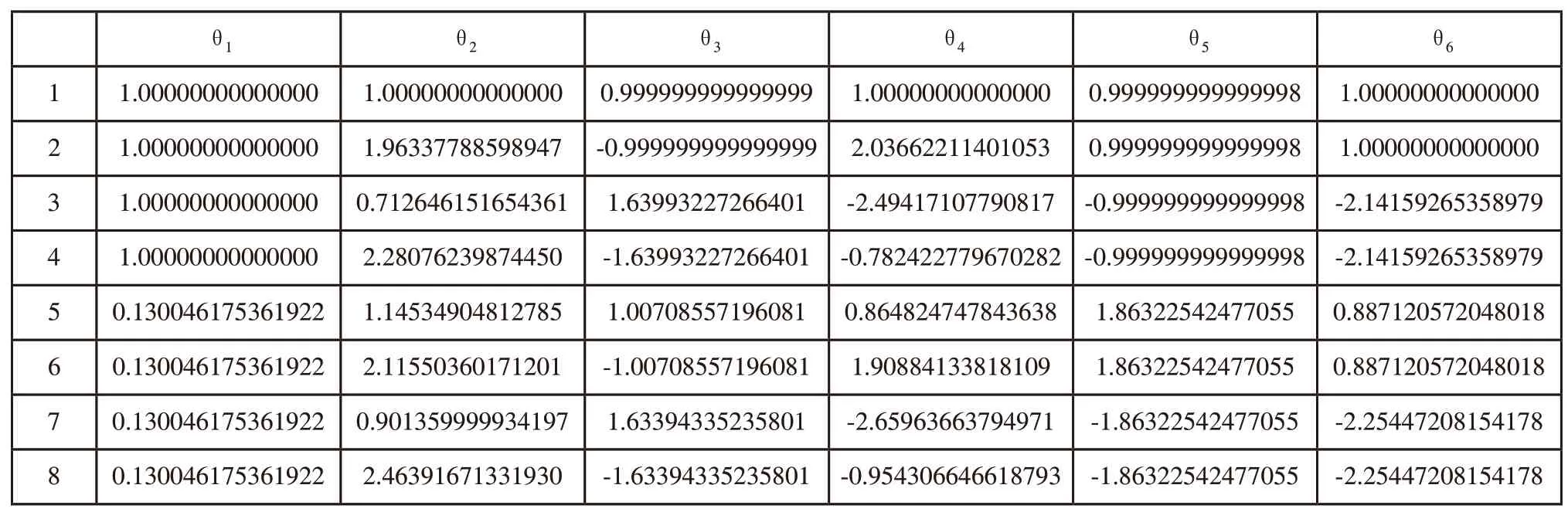
表2 UR10Θ=[1,1,1,1,1,1]时末端逆解
3.2 奇异点预测验证
算例二设计了如图3所示的程序结构,以此验证对示教轨迹奇异位形及不可达点的预测。check_singularity节点实现了2.3中的预测算法。其中,通过ur_modern_driver的/joint_states获得UR10的实时关节位置信息,并通过main_control的服务请求消息,得知当前运动指令及运动方向,并将计算结果通过服务响应返回给main_control,若响应内容为预测到奇异位置或将抵达不可达预测点时,main_control通过29999端口向机器人发送停止命令。

图3 奇异点预测节点与主控节点的话题服务通信
相关的设置参数如下:位移前瞻POS_MAX_PROSPECT=40mm;位移步长POS_MIN_STEP=5mm;旋转角前瞻ORI_MAX_PROSPECT=10×M_PI/180rad;旋转步长ORI_MIN_STEP=2*M_PI/180rad;奇异判断阈值SINGULARITY_THRESHOLD=0.4rad;起点Θ=[-83.8852,-48.272,-122.884,-100.159,91.5561,6.0538];运动方向IS_POSITIVE=TRUE;运动自由度JOG_INDEX=2(Y轴);参考坐标系REF_COORD=BASE(基坐标);速度比VEL_OVERRIDE=100%;运动过程机器人末端位置将穿过在一、二轴构成的平面即奇异位形,实际的关节位置跟踪和预测对比图如图4所示,关节轴1速度对比如图5所示。根据图4可看出预测算法对轴关节未来趋势的准确预计;图5中T=2.691s,实际检测关节速度vel=20.15degree/s2,预测关节速度远远大于电机可执行范围,即预测到穿越奇异位形,此时check_singularity节点终止预测,main_control收到异常,并向机器人发送停止脚本,机器人在T=2.91s安全停止,未触发保护性停止等断电行为。
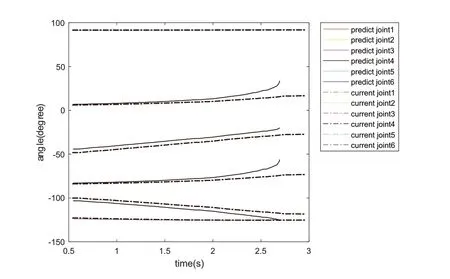
图4 位置示教遇奇异位形实际关节位置与预测对比图
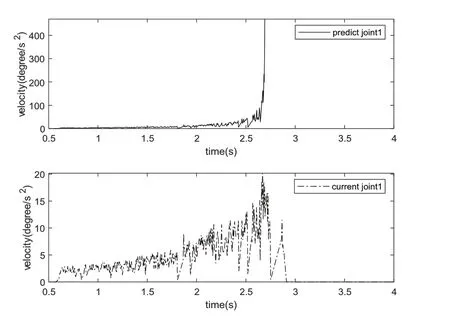
图5 位置示教遇奇异位形实际轴关节1速度与预测对比图
4 结语
由图4、图5可见,在不干扰原本示教控制前提下,经过文中设计的方法,可提前预知奇异位形及不可达点等信息,及时有效地避免机器人因尝试穿越奇异位形,导致个别关节轴的高速旋转而引起的保护停止。经过改进后的控制操作体验度大大提升,加快了调试速度,提高了作业效率。
