中间支撑刚度对双跨梁屈曲稳定性的影响
2022-06-17毛晓晔邵志华陈立群
毛晓晔, 邵志华, 舒 送, 范 鑫,3, 丁 虎, 陈立群
(1.上海大学 力学与工程科学学院 上海市应用数学和力学研究所,上海 200444;2.中国人民解放军第5720工厂,安徽 芜湖 241007;3.中国科学技术大学 精密机械与精密仪器系,合肥 230026)
管路系统是保障飞机飞行安全的最重要系统之一,其振动问题在使役过程中十分突出。飞机管路系统经常发生各种类型的故障,主要表现为管路系统振动故障,影响飞行安全,造成严重损失[1-2]。Gao等[3]综述了2020年以前关于飞机管道故障以及减振的相关研究进展:根据美国统计,燃油、空气和液压管路系统的故障占飞机部件故障总数的50%~60%;据俄罗斯统计,燃油、润滑油和液压系统故障也占飞机故障总数的50%以上;近年来,我国飞机液压管路系统也发生了多起振动故障,这些问题一直困扰着飞机设计者。
关于飞机液压管路建模方法已有大批学者展开了广泛研究,常见的管道模型大致分为三种[4],分别是Euler-Bernoulli模型[5],Timoshenko模型[6-7]以及壳模型[8-9]。基于这些模型,可以研究管道的受迫激励[10-11],参激共振[12-13]等动力学响应问题。这些管道模型理论研究表明:对于短粗管道,必须使用Timoshenko模型描述管道动力学;对于大管径薄壁管道,则必须使用壳模型;而对于长径比较大的细长管道,则一般使用Euler-Bernoulli模型进行分析。不管哪种模型,在轴向流速达到临界值后,管道的直线平衡位形会失稳发生分岔现象[14-15]。在屈曲状态下,管道会变为本质非线性,并且会产生双稳态势阱间跳跃的剧烈振动[16-17]。而这种流速改变结构本征特性的现象已经被美国航空航天局NASA实验验证[18]。工程中,除了流速会引起管道屈曲,管道上存在的压力也会改变结构本征特性。例如环境温度升高造成管道热膨胀而产生轴向压力,安装操作中施加的旋紧压力以及管道尺寸偏差带来的压力等,这些压力都可能导致管道产生屈曲,因此对于管道的压力不容忽视。
以上研究都是基于单跨管道进行的,在很多实际工况下,较长的管道需要在中部安装卡箍或夹具,这些往往都是弹性约束,建模时可以简化成具有一定刚度的弹簧[19-21]。例如,Gao等[22]提出了一种针对飞机长距离多支承液压管路振动分析的模型, 通过引入人工弹簧模拟边界条件,提出了一种有效的管道模型简化求解方法,而且研究结果表明,该方法能够显著降低计算成本,且具有足够的计算精度;而赵小颖等[23]在建模时直接将弹性支承力用Delta函数表示在结构控制方程中。不过,他们对于多跨结构的屈曲以及屈曲稳定性并未讨论。
本文仅考虑压力对管道屈曲的影响,并且低速流体对结构本征特性的影响并不显著,因此建模过程中暂时忽略流体作用,将管道简化为带中间弹性约束的梁模型。以分段以及整体两种方式,建立结构横向振动控制方程。通过对比两种模型,证实整体梁模型的精确性。在此基础上进一步分析了双跨梁的静力学屈曲分岔现象,并得到了弹性约束对结构屈曲临界状态的影响作用。
1 数学模型
对于双跨梁,有两种建模方式。由于梁是一个连续体,可以将中间支撑所带来的约束力作为梁上的集中力考虑;同时,也可以将梁分为两段考虑,将中间支撑约束作为边界考虑。第一种方法所建立的模型简洁,用集中力表达支撑约束;第二种方法所建立的模型精细,用边界连续性条件表达梁的整体性。考虑到计算简洁,本工作将使用第一种模型进行分析计算,用第二种模型验证第一种模型的精确性。
1.1 整体梁建模
整体梁分析模型,如图1所示。静态梁两端铰支点的距离为L,中间位置有一刚度为k的弹性支撑。梁的材料密度为ρ,横截面积为A,杨氏模量为E,横截面关于中性层的截面惯性矩记为I。梁受到轴向压力P,建立该梁的面内振动模型,令梁上任意处的横向位移记为w(x,t),轴向位移记为u(x,t)。

图1 整体梁分析模型示意图Fig.1 Schematic diagram of the continuous beam model
根据能量法建立运动方程。其中,T为梁的动能,U1为梁的势能,U2为中间支撑弹簧势能。则系统动能、势能积分表达式分别为
(1)
式中:δ表示狄拉克函数;下标中量符号之前的逗号表示该量符号的偏导数;动能表达式包含梁纵向运动和横向运动的动能。梁的势能U1中,第一项是由中性面拉伸产生的势能,第二项是弯曲所产生的势能,第三项是与轴向压力P有关的拉压势能。
将式(1)代入Hamilton变分原理

(2)
式中,ζ表示指定时间间隔内的变化量。
结合纵向位移远小于横向位移,可降维得到考虑几何非线性的梁的积分-偏微分控制方程
(3)
以及对应的边界条件
w(0,t)=w(L,t)=0,
w,xx(0,t)=w,xx(L,t)=0
(4)
忽略非线性项可得派生系统为
(5)
由于该模型受简支边界条件约束,可以假设上述方程的解为
(6)
代入控制方程得到
(7)
记式(7)等号左边为Gn(x,t),则n阶Galerkin截断可写为
(8)
以此得到n个含有未知数qi(t)的常微分方程组,再令其中
qi(t)=Qieiωt,i=1,2,…,n
(9)
化简后可得到方程组矩阵为
(H+K)Q=0
(10)
式中:H表示n阶对角矩阵;K为n阶刚度矩阵;Q为n阶列向量。
(11)
(12)
(13)
(14)
若使式(10)有非零解,则系数矩阵H+K行列式值必然等于0。代入模型参数,对于给定的轴向压力P和约束刚度k,即可得到相对应的频率ω。
1.2 分段梁建模
双跨耦合模型,如图2所示。

图2 双跨耦合模型示意图Fig.2 Schematic diagram of the double-span beam model
考虑到双跨梁为对称结构,可选取一侧用能量法进行建模。一边铰支、一边弹性约束的复杂边界梁对应的动能、势能为
(15)
根据Hamilton变分原理得到的复杂边界约束梁的控制方程为
(16)
忽略其中的非线性项,得到派生方程
ρAwn,tt+EIwn,xxxx+Pwn,xx=0,n=1,2
(17)
记左边梁为1,右边梁为2,则w1表示1梁的横向位移,w2表示2梁的横向位移,两者控制方程相同。
两段梁对应的边界条件和耦合连续条件为
w1,xx(0,t)=0,w1(0,t)=0,
(18)
通过分离变量法,设控制方程的解为
wn(x,t)=φn(x)eiωt,n=1,2
(19)
将其代入控制方程得到
EIφn(x),xxxx-ρAω2φn(x)+Pφn(x),xx=0
n=1,2
(20)
设上述4阶常微分方程的解为
φn(x)=Aneλ1x+Bneλ2x+Cneλ3x+Dneλ4x
n=1,2
(21)
其中参数λ1,2,3,4为
(22)
将控制方程的解代入边界条件和连续条件,可以化简得到
MNT=0
(23)
式中:M为8阶系数矩阵;N为8阶列向量。
N=[A1B1C1D1A2B2C2D2]
(24)
其中
(25)
若方程有非零解则需要使系数矩阵M行列式为0,由此得到关于刚度k,压力P以及频率ω的关系式。给定中间约束刚度k,便可得到固有频率ω随轴向压力的变化。
3 模型验证
由式(18)可见,分段梁模型在中间支撑处可以严格表达剪力的突变,因此该模型精度更高。不过,该模型涉及到非齐次边值问题,动力学响应求解复杂。而整体梁模型虽然不能严格表达中间支撑处的剪力突变,但是合理的截断阶数将会使该模型足够接近真实条件。这里将从固有频率的角度,对整体梁模型进行验证,模型参数如表1所示。

表1 模型材料尺寸参数Tab.1 Parameters of the beam
整体梁在计算固有频率时采用了Galerkin截断,首先有必要讨论其自身截断收敛性,再将收敛的结果与分段梁得到的结果进行对比验证。图3展示了4阶和6阶截断条件下,不同中间支撑刚度所对应的固有频率随轴力的变化,可见在所关注刚度范围内,4阶截断已经具备较高的收敛性。

图3 整体梁模型的截断收敛性Fig.3 The truncation convergence of the continuous beam model
在整体梁自身截断收敛性得到验证后,图4(a)~(d)对比分段梁模型和4阶截断整体梁模型所得到的不同刚度条件下,前4阶固有频率与轴力之间的关系。观察到虽然两种建模方式不同,但是两种模型得到的频率几乎完全拟合,这说明收敛的整体梁模型具有合理的精度表达中间支撑刚度所引起的梁固有特性的改变。
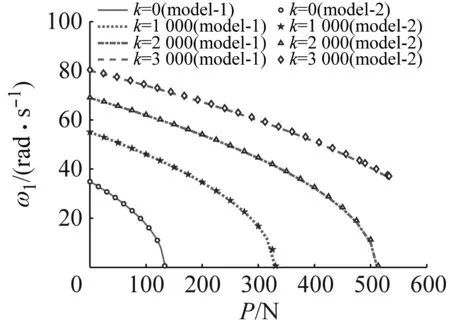
(a) ω1随轴力的变化

(b) ω2随轴力的变化

(c) ω3随轴力的变化

(d) ω4随轴力的变化
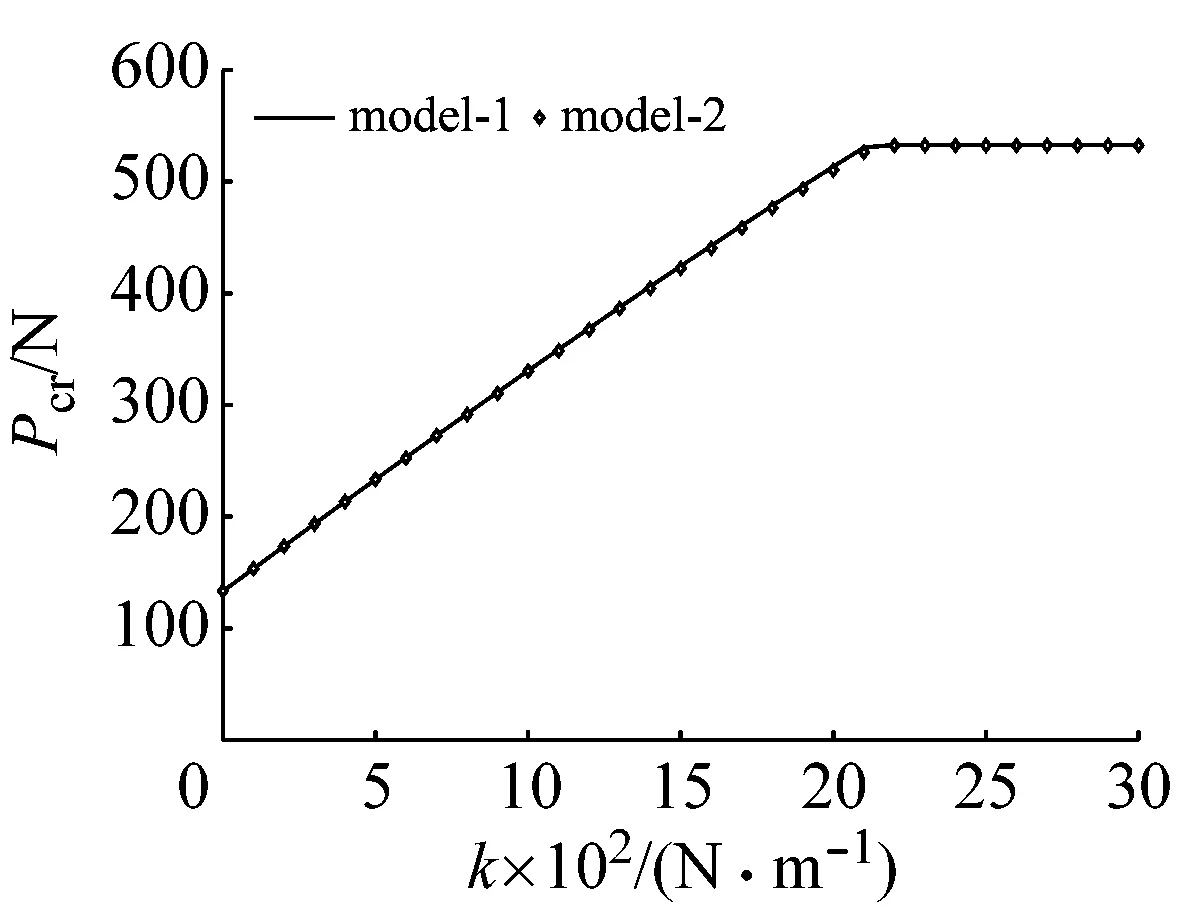
(e) Pcr随支撑刚度的变化图4 两种梁模型的对比验证Fig.4 Comparison and verification of the two beam models
当轴力足够大时,固有频率会变为0,此时发生屈曲失稳。图4(e)则对比了两种模型分析得到的临界轴力,可见中间约束刚度的增加首先会提高临界状态对应的屈曲力,但是当刚度达到一定大小以后,这种对临界轴力的放大作用消失,最终收敛于半长简支梁的临界屈曲压力。
由于已经验证了4阶截断整体梁模型的收敛性和精度,可以在4阶截断基础上推导出一阶屈曲轴力为
(26)
当弹簧约束刚度为0时,可退化得到压杆的Euler定理Pcr=π2EI/L2;而当约束刚度足够大时,一阶临界压力为Pcr=4π2EI/L2。
2 屈曲位形
如果梁所受轴向压力超过临界屈曲值,就会发生屈曲失稳,表现为直线平衡位形失去稳定,固有频率变为0。在非线性项的作用下,梁会出现曲线平衡位形,也叫非平凡静平衡位形。第1章已经验证了整体梁模型的精确性,由于计算简洁,本章将以该模型为基础,计算不同中间支撑刚度下,双跨梁的屈曲位形变化。
由于位形函数只与空间坐标有关,因此忽略控制方程中显含时间的项与激振力项,整理可得位形满足的方程为
(27)
以及对应的边值条件

(28)
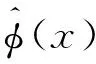
(29)
分别取n=4,6进行截断,将式(29)代入式(27)中,方程两端同时乘以权函数sin(jπx/L),并对x进行从0~L的积分,得到关于系数Bk(k=1…n)的n阶方程组。为了便于不同刚度下的对比,选取轴向力P=101%Pcr,刚度和对应压力值的选取参数如表2所示,模型其他参数值见表1。

表2 模型弹性支承刚度和对应的压力值Tab.2 The bearing stiffness and the pressure
联立n个截断方程,计算参数B1~Bn的取值,便可得到不同刚度、不同截断阶数所对应的屈曲位形系数。
2.1 截断收敛性随支撑刚度的变化
第一章已经通过对比验证得到,在自身收敛的条件下,整体梁模型可以拥有合理的精度近似描述中间支撑刚度引起的剪力突变。因此,在计算屈曲位形时,依然必须对截断的收敛性进行判定。然而,由于式(27)中非线性项的存在,过大的收敛阶数下,软件直接计算位形系数会变得非常困难。不过,考虑到屈曲位形的解必然存在,高阶截断也仅仅是对低阶截断的修正,于是考虑利用4阶截断的位形系数作为迭代初值,使用牛顿迭代法,进行高阶截断位形系数的计算。
记截断后得到的n个关于位形系数B=(B1,B2,…,Bn)T的多元非线性代数方程为F=(f1,f2,…,fn)T,写为矩阵形式
F(B)=0
(30)
代入牛顿迭代公式,则有
B(k+1)=B(k)-J[F(B(k))]-1F(B(k)),
k=1,2,…,n
(31)
其中J[F(B(k))]-1是式(30)的Jacobian矩阵的逆矩阵,记
(32)
当满足ε<1×10-10时,输出结果B,计算流程如图5所示。

图5 高阶屈曲位形系数计算流程图Fig.5 Flow chart for calculating higher order flexural configuration coefficients
从4阶截断求得的屈曲位形开始计算,系数如表3所示。可见对于一阶屈曲位形,仅有奇数阶模态上存在非0系数;而对于二阶屈曲位形,仅二阶模态上存在非0系数。4阶截断所得到的前两阶屈曲位形如图6所示,每阶屈曲位形都存在对称的两组解,为图形清晰,后续屈曲位形图形仅画出其中一组结果。

(b) 第二阶正负屈曲位形图6 4阶截断处理不同刚度作用下前两阶临界屈曲位形Fig.6 The first and the second order critical buckling configuration with different stiffness under the fourth order truncation treatment

表3 前两阶屈曲位形系数(截断阶数n=4)Tab.3 Coefficients of the first and the second order buckling configurations (truncation order n=4)
除4阶截断求得的一阶正位形的位形系数B1~B4,其他系数初值均取0,以此作为初值。利用上述迭代方法,可以得到不同刚度、不同截断阶数下的位形系数,得到的位形曲线如图7所示。可以看到,刚度k=1 000时,12阶截断可满足其收敛性;刚度k=2 000时,16阶截断可满足位形收敛性。可见,对于一阶屈曲位形,约束刚度越大,对收敛阶数的要求会越高。

(a) k=0

(b) k=1 000 N/m

(c) k=2 000 N/m图7 不同截断阶数下第一阶屈曲位形Fig.7 Comparison of the first order buckling configurations under different truncation orders
同样,取4阶截断求得的二阶位形系数中的一组作为初值,其他系数初值也依然设置为0,经迭代后,得到不同刚度系数、不同截断阶数下的二阶位形系数,如图8所示。显然,二阶屈曲位形上,截断的收敛性不受中间刚度变化的影响。并且,即便使用更高的截断阶数,二阶位形系数中也仅二阶模态系数不为0,即二阶屈曲位形仅需二阶模态即可严格表达。

(a) k=0
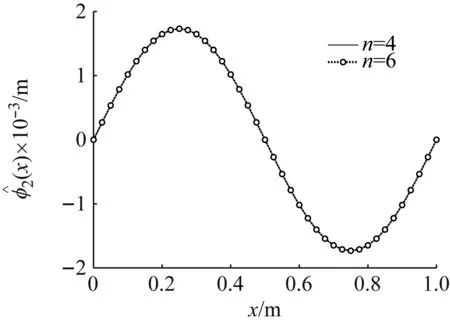
b) k=3 000 N/m图8 不同截断阶数下第二阶屈曲位形对比Fig.8 Comparison of the second order buckling configuration under different truncation orders
2.2 屈曲位形随支撑刚度的变化
图9将不同刚度下收敛的屈曲位形进行对比,可以看到,刚度对前两阶的屈曲位形影响都很大。随着刚度增加,二阶位形会受到弹性约束而减小,一阶屈曲位形会变大。特别对于一阶屈曲位形,随着约束刚度的增加,原本只有一阶系数项非0的屈曲位形,逐渐受到三阶系数项的作用而远离半周期正弦函数,而且刚度越大,这种改变越明显。而刚度在达到3 000 N/m时,一阶屈曲位形产生本质性改变,表现出反曲现象。这需要对位形的稳定性进行分析,以厘清这些复杂现象的真实性。

(a) 第一阶正屈曲位形

(b) 第二阶正屈曲位形图9 不同刚度作用下前两阶收敛屈曲位形对比Fig.9 Comparison of the first and second order convergent buckling configuration under different stiffness
3 位形稳定性分析
第二章对屈曲位形的计算中,不同支撑刚度条件下都会出现多组屈曲位形系数的实数解,不过它们并不一定都是稳定的,本章将对前两阶屈曲位形的稳定性进行讨论。以收敛的截断阶数,计算屈曲位形稳定性随中间支撑刚度的变化。
3.1 稳定性的数学判断
为进一步研究屈曲稳态构型周围的振动特性,首先作如下坐标变换

(33)
将式(33)代入控制方程(3),并结合屈曲平衡方程(27),得到关于v(x,t)的非平凡位形基础上的振动控制方程
(34)
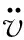
(35)
选取符合边界条件的多自由度横向位移表达式
(36)
将式(36)代入式(35),两端同乘以sin(jπx/L)并进行对应收敛阶数的截断,得到非平凡位形上的n阶未扰系统方程组
(37)
将式(37)改写为
(38)
其中
y=q
(39)
进而求得该系统的2n阶Jocabian矩阵

(40)
式中:E为n阶单位矩阵;M为系数矩阵,是关于参数P,k,E,L,I,ρ以及B1~Bn的n阶对称矩阵。
根据λE-J得到矩阵J的特征方程,以及对应的平衡点系数,解出特征值λn。利用常微分方程平衡点稳定性知识可知,当该平衡点的一系列特征值中存在正实部时,平衡点不稳定。
图10、图11以及图12分别给出了中间支撑刚度为1 000 N/m、3 000 N/m以及100 000 N/m时平凡位形以及前两阶非平凡位形的特征值稳定性分析。从图10可以看出,随着轴力的增加,平凡位形在超过临界轴力后失稳,而一阶非平凡位形变得稳定;与此同时,二阶非平凡位形特征值虽然会产生变化,但正实部一直存在,即在中间支撑刚度为1 000 N/m时,二阶非平凡位形一直是不稳定的。
(a) 直线位形稳定性
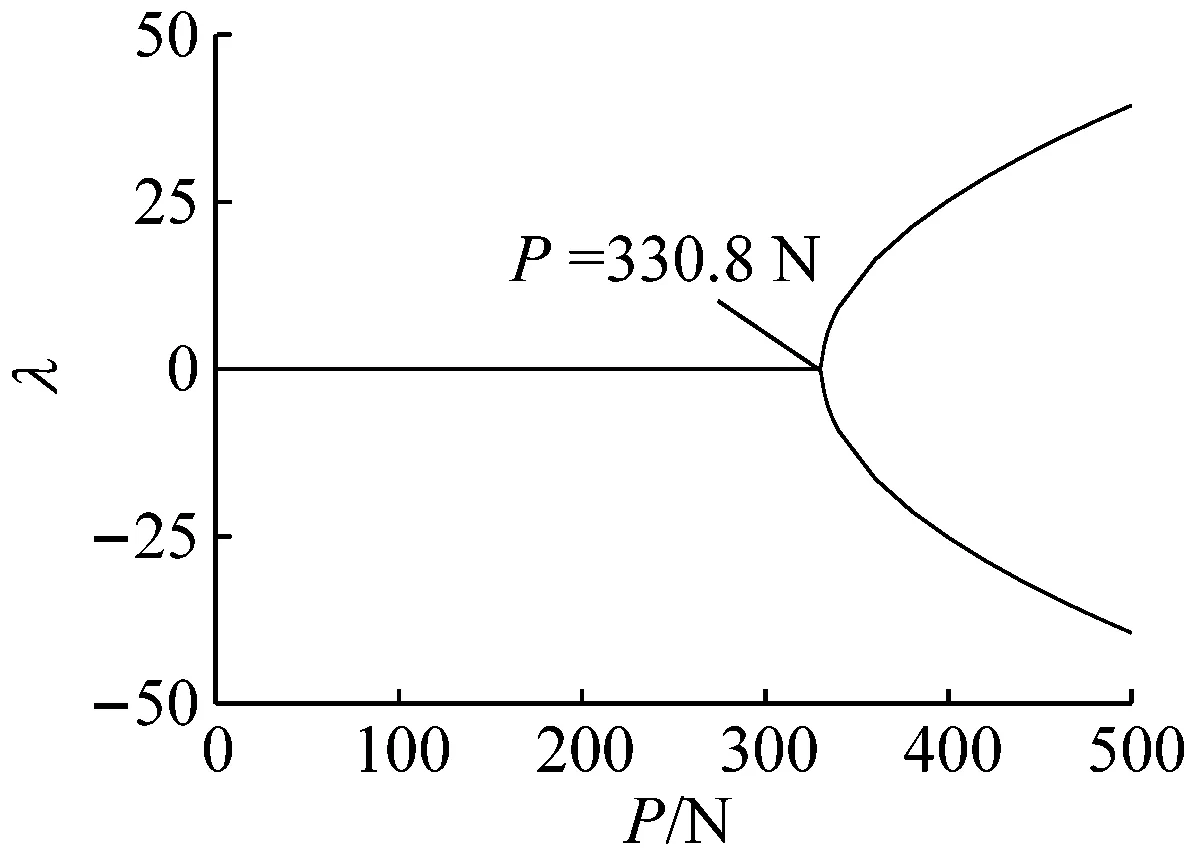
(b) 一阶非平凡位形稳定性

(c) 二阶非平凡位形稳定性图10 k=1 000 N/m时位形稳定性随轴力的变化Fig.10 Stability of the configuration solutions changing with the axial force while the bearing stiffness is 1 000 N/m
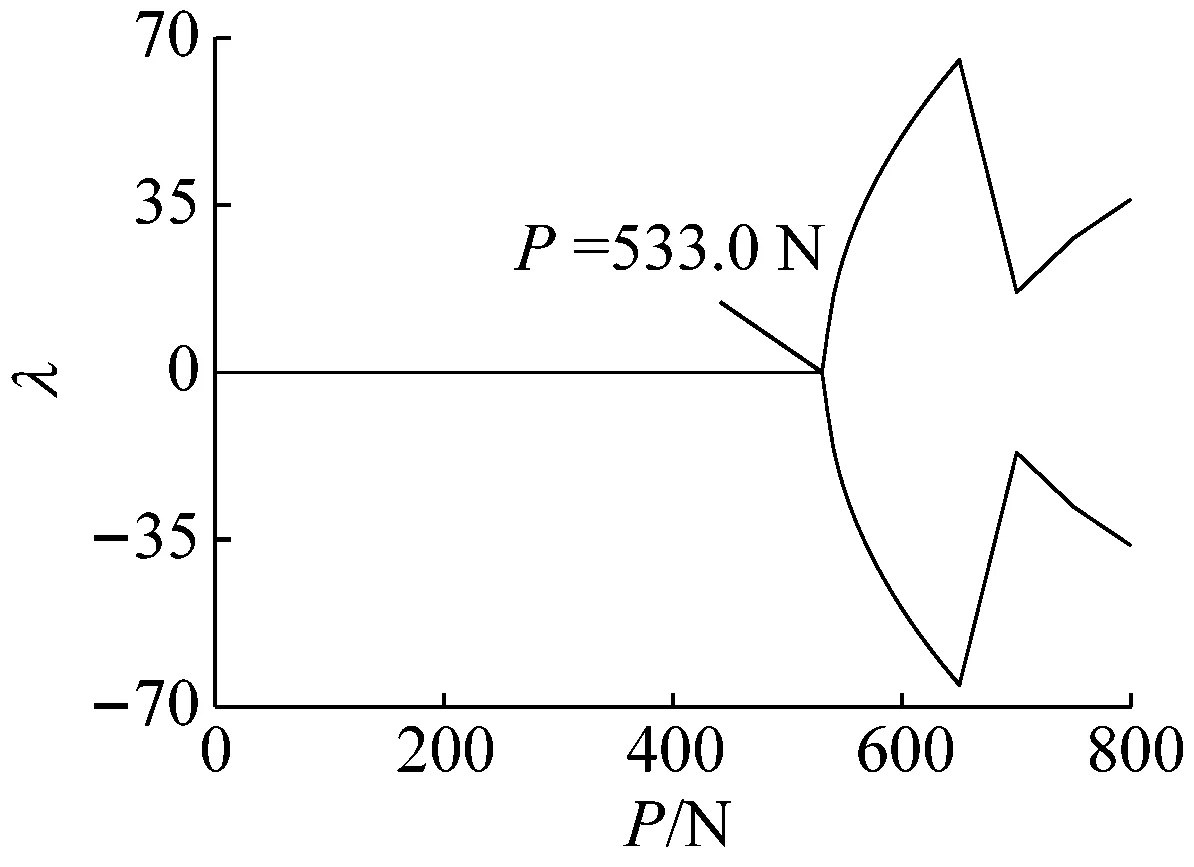
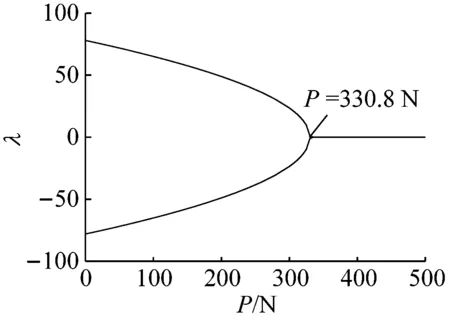
(a) 直线位形稳定性
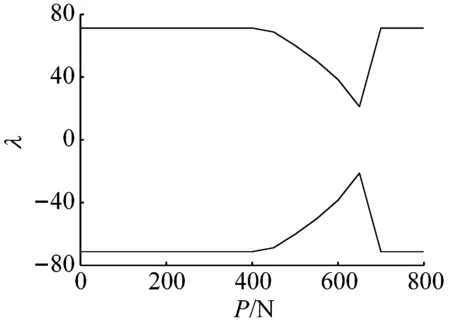
(b) 一阶非平凡位形稳定性

(c) 二阶非平凡位形稳定性图11 k=3 000 N/m时位形稳定性随轴力的变化Fig.11 Stability of the configuration solutions changing with the axial force while the bearing stiffness is 3 000 N/m
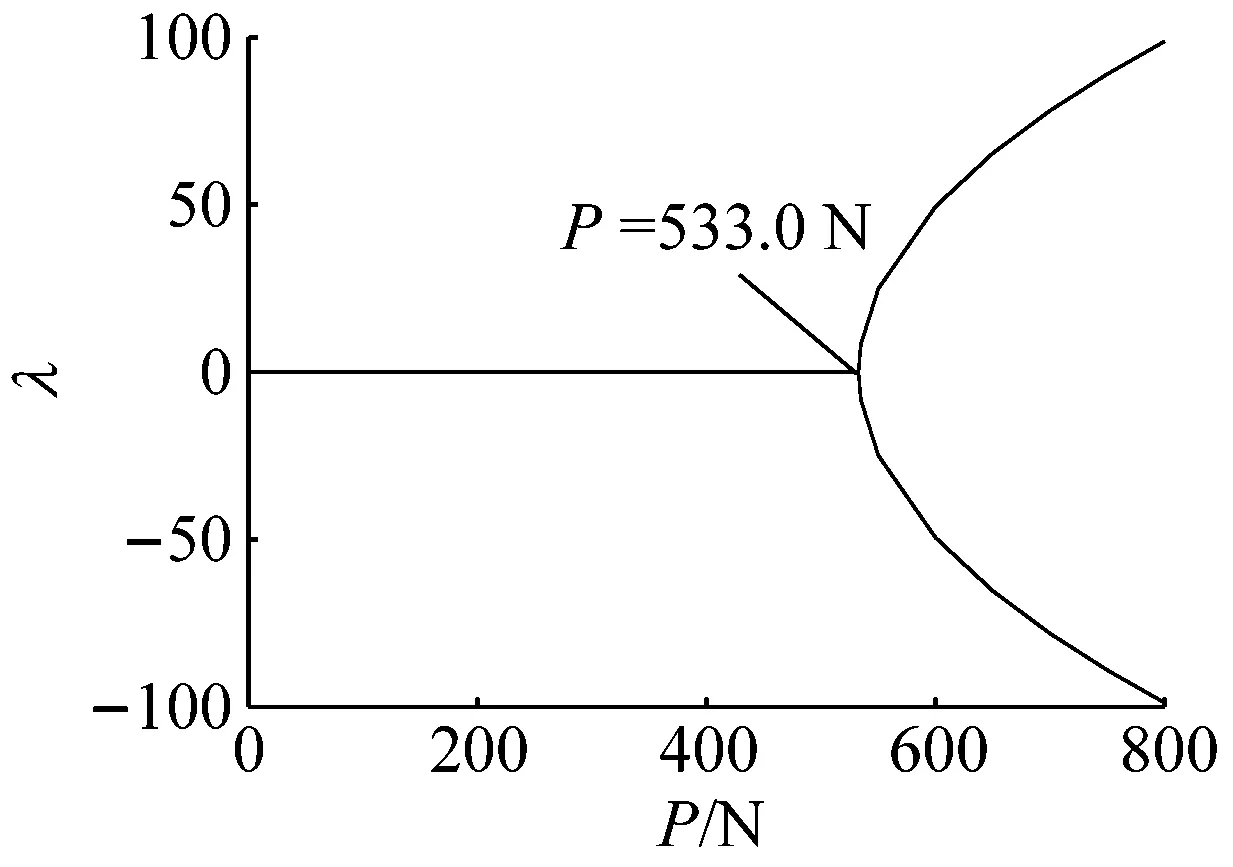
(a) 直线位形稳定性

(b) 一阶非平凡位形稳定性

(c) 二阶非平凡位形稳定性图12 k=100 000 N/m时位形稳定性随轴力的变化Fig.12 Stability of the configuration solutions changing with the axial force while the bearing stiffness is 100 000 N/m
从图11可以看出,当中间支撑刚度较大时,平凡位形在超过临界轴力后变得不稳定,而二阶非平凡位形变得稳定。此时,虽然一阶非平凡位形特征值产生变化,但是正实部一直存在,一阶非平凡位形不稳定。
从图12可以看出,当中间刚度近似于无穷大以后,位形的稳定性情况与刚度达到3 000 N/m时变化相同,屈曲以后从直线位形直接过渡到二阶非平凡静平衡位形达到稳定,说明此时稳定性不再随刚度产生变化。
由以上对比可以得知,虽然非平凡位形有高阶多解,但是给定轴向压力和约束刚度下能够满足稳定的位形有且仅有只有一组(非平凡位形上下对称,意义相同)。刚度较小时,压力达到临界值会由稳定的直线位形叉形分岔到稳定的一阶非平凡位形。而在刚度较大时,临界压力作用下会使梁由直线位形直接分岔至稳
定的二阶非平凡位形;而发生这一转换的刚度临界值即为式(26)推导得到的k=45EIπ4/28L3,代入参数后,此模型下的数值约是k=2 113 N/m。
3.2 一阶非平凡位形稳定性的物理解释
对于不同支撑刚度条件下,一阶非平凡位形的稳定性可以从物理角度进行解释。对一阶非平凡位形函数求二阶导,即可得到屈曲位形的曲率表达式。如图13所示,刚度为0、1 000 N/m以及2 000 N/m时,其曲率在整个梁上任一点均是同号的。但是刚度达到3 000 N/m时,中间位置曲率出现异号。从不同支撑刚度下一阶非平凡位形曲率的变化可以判断,当中点处曲率等于0时,所对应的支撑刚度为临界刚度。超过该刚度后,一阶非平凡位形失稳,而平凡位形会直接分岔至二阶非平凡位形。
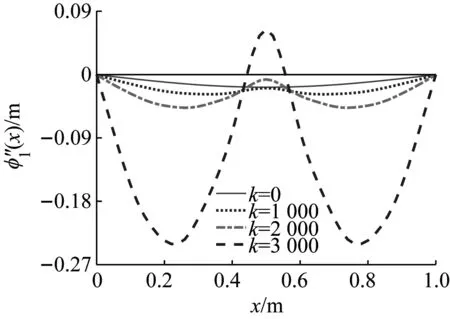
图13 不同刚度下一阶非平凡位形的二阶导数Fig.13 Second derivatives of the first-order nontrivial configurations with different bearing stiffness
4 结 论
以上工作通过两种建模方式得到了带中间弹性支撑的轴向受压双跨梁的运动控制方程,并在连续梁模型的基础上,对中间支撑刚度的影响进行了详细研究,得到以下结论:
(1) 连续梁模型的模态虽然处处连续可导,但经过足够多的模态叠加,连续梁模型可以以合理的精度描述中间支撑处的剪力突变。
(2) 一阶屈曲位形随支撑刚度的增加远离半周期正弦函数,并且需要使用更高阶截断才能使用连续梁模型得到收敛的屈曲位形。当中间支撑刚度超过临界值后,一阶屈曲位形失稳,物理表现为屈曲位形曲率出现异号。
(3) 二阶屈曲位形截断收敛性不受中间支撑刚度影响,仅使用单周期正弦函数即可精确描述二阶屈曲位形。而当支撑刚度超过临界值后,二阶屈曲位形变得稳定,此时中间弹性支撑等同于节点。
