基于旋量理论的四自由度抓取机械手奇异位形分析

刘青松，袁 杰，钱建华

（中科华核电技术研究院有限公司，广东 深圳 518124）

基于旋量理论的四自由度抓取机械手奇异位形分析

刘青松，袁 杰，钱建华

（中科华核电技术研究院有限公司，广东 深圳 518124）

机构奇异位形是影响机构运动学性能的重要因素之一，机械手的奇异位形可导致机构锁死、控制复杂化、危害人员安全等问题．本文针对四自由度抓取机械手采用旋量理论对该机械手进行了运动学分析，并推导出了机械手奇异位形，采用随机取点法验证了旋量方法的可行性．在此基础上，利用MATLAB Robotics对奇异位形进行了仿真分析．仿真结果表明，应用旋量理论求解的奇异位形数据准确，可有效剔除机械手奇异位形，确保机械手高速准确完成抓取任务．

奇异位形；机械手；旋量理论；随机取点法

机器人运动学是机器人性能分析、动力学分析以及精确控制的基础，具有非常重要的地位[1-3]．机构奇异位形是影响机构运动学性能的重要因素之一．机械手的奇异位形可导致机构锁死、控制复杂化、危害人员安全等问题．目前，研究奇异位形的方法主要有Grassmann线几何法、运动学法、代数法等[4]．其中，线几何法需要对每根连杆轴的线矢进行分析，求取子问题过多；运动学法运用运动学上的基本定理，找到物体运动的速度关系，对于空间运动的物体，3点速度关系不易求取；代数法运用DH法则对每个连杆建立局部坐标系，求取速度雅克比矩阵，其求取过程中采用局部参数，存在表示不足的问题．

本文分析了轮式移动四自由度机械手，该机械手需高速准确地完成地面异物抓取等复杂任务，考虑到轮式移动平台不能实现全方位移动，因此，机械手的奇异位形不可避免，分析其奇异位形种类，对提高其作业性能具有重要意义．本文以旋量理论从整体上建立了机械手的运动学模型，求解了速度雅克比矩阵，通过旋量理论分析了操作空间中速度参数之间线性关系，推导出了机械手奇异位形[5]，并采用广泛应用的随机取点法验证了该方法可行性．在此基础上，利用MATLABRobotics对奇异位形进行了仿真分析．

1 四自由度机械手运动学分析

本机械手是由4个转动副连接，4个杆件组成的4轴串联机器人，融合了腰部回转、肩部内旋/（外翻）、肘部内旋/（外翻）、腕部回转、手指屈/（伸）等各关节运动，如图1所示．

图1 4-DOF机械手坐标系Fig.1 4-DOFmanipulator coordinate system

1.1 运动方程的建立

如图1所示，建立四自由度机械手基坐标系 {S}和工具坐标系 {T}，图所示为初始位形时[6]．

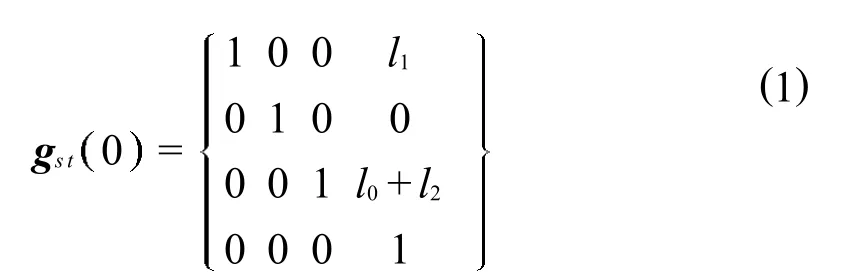
各个关节的运动旋量：

于是，得到正运动学方程：

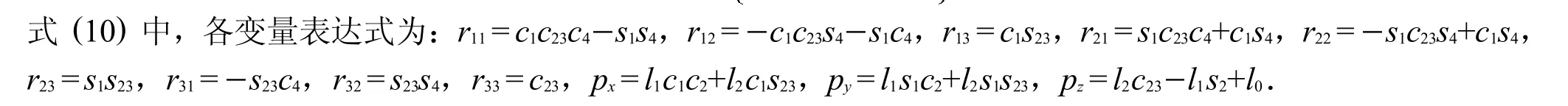
1.2 雅克比矩阵求取

机械手速度雅克比矩阵只需通过运动旋量的位置和方向确定：

式 (11)中各当前位形下各个关节对应的运动副旋量坐标：

于是，得到四自由度机械手的速度雅克比矩阵：

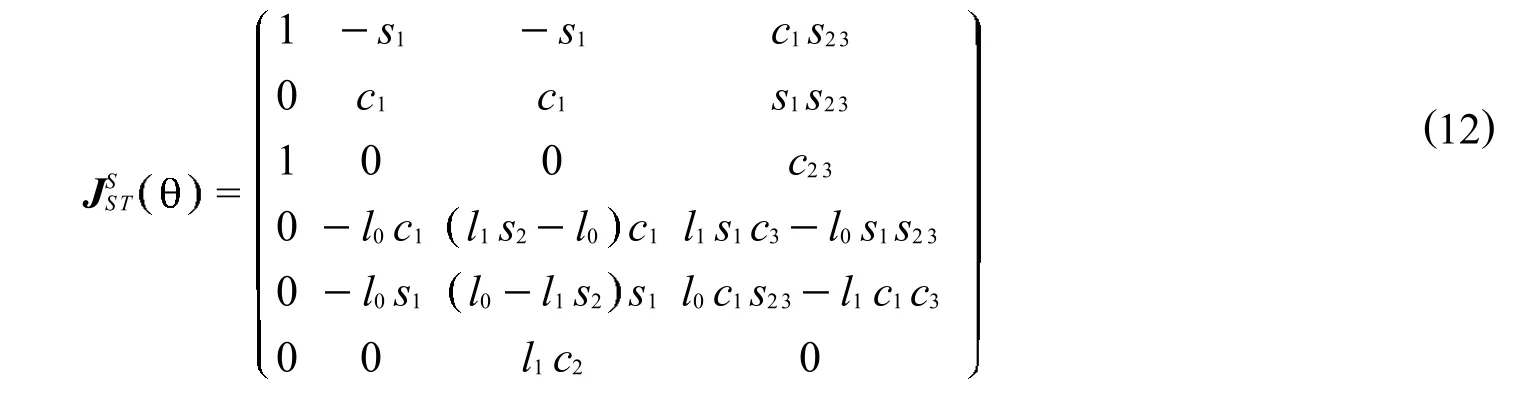
2 奇异位形求取

2.1 旋量法求取奇异位形

上一小节已经得到机械手的速度雅克比矩阵，当雅可比矩阵的秩比操作空间向量维数小时，机械手会出现奇异位形[7]．

本文采用旋量方法求取奇异位形，与代数方法相比，它无需对雅克比矩阵求逆，计算更简便；其通过分析空间速度矢量与关节速度矢量的线性关系，剔除线性相关的速度矢量，从而得到饱含独立速度矢量的雅克比矩阵．该方法适用于少自由度机械手（自由度少于6）的奇异位形求解．

旋量理论中有一种重要运算，称为互易积．它表示运动旋量和力旋量的约束关系．运动旋量用来表示刚体的运动，力旋量表示刚体受到的力，两者的互易积表示力旋量对运动旋量所作的功．当互易积为0时，即力旋量对运动旋量的瞬时功率为0，无论旋量中力或力矩多大，不会对刚体做功，不改变该约束作用下刚体的运动状态，将此时的力旋量记作与运动旋量所对应的反旋量[8]．通过反旋量对雅克比矩阵中的运动旋量进行互易积运算，可以构造操作空间6个速度矢量 wxwywzvxvyvzT的线性方程组，由于自由度小于6，必然存在自由变量，可以找到最大线性无关向量组，即对应饱含独立速度矢量的雅克比矩阵[9]．

已知雅克比矩阵，通过反旋量构造线性方程组：

由于vx，vy为自由变量，剔除这2个元素所对应的雅克比矩阵行向量，得到饱含独立速度矢量的雅克比矩阵为

当det Jst=0或det Jst= 时，机械手出现奇异位形．

根据关节角运动范围，得到奇异位形为：2= 90°，3=90°．

2.2 随机取点法求取奇异位形

旋量方法已经推导出了机械手的奇异位形，为了验证该方法的可行性，本文采用基于代数法的的随机取点法对求解结果进行了验证求取．随机取点法是利用概率统计的原理，首先建立1个概率模型或随机过程，使其参数等于问题的解；然后通过观察模型或进行抽样试验来计算所求参数的统计学特征；最后得到所求问题的近似解．建立数学模型：．imin为关节转角最小值，imax为关节转角最大值，rand 1为随机数．

本文利用随机取点法分析了各关节变量运动范围内，各关节转角与雅克比矩阵分解出的最小奇异值的关系，如图2所示．当最小奇异值为0时，即出现奇异位形[7]．

从图中不难发现，关节角1和关节角4不存在奇异位形，关节角2和关节角3存在奇异位形．关节角2的奇异位形出现在图中第50个点．结合图中公式计算得2= 90°；关节角3的奇异位形出现在图中第250个点和第750个点，结合图中公式计算得2=90°，3= 90°．由于时与车体发生干涉，因此，机械手的奇异位形为2= 90°，3=90°，与应用旋量方法求得的结果一致．

图2 关节角1与最小奇异值的关系Fig.2 JointAngle1withminimum singular value

图3 关节角2与最小奇异值的关系Fig.3 JointAngle2withm inimum singular value

图4 关节角3与最小奇异值的关系Fig.4 JointAngle3withminimum singular value

图5 关节角4与最小奇异值的关系Fig.5 JointAngle4withminimum singular value

3 奇异位形分析

广义上讲，奇异位形主要分为边界奇异位形和内部奇异位形[10]．机械手只要远离工作空间边界即可避免边界奇异位形；但机械手处于内部奇异位形时，会使工作空间变小，灵活性变差，可达区域变得“崎岖”，引起实际操作自由度的瞬时减少，无法实现沿着某些方向的运动，造成机构锁死，从而无法实现作业任务；与此同时某些关节角速度会趋向无穷大，引起控制复杂化，甚至有失控的危险[11]．从求取过程中可知，奇异位形的出现与各关节角的变化组合密切相关，只要出现奇异位形，四自由度机械手运动性能就无法保证．

采用仿真软件MATLAB Robotics对奇异位形进行仿真，四自由度机械手出现奇异位形时，其位置和姿态如图6所示．

图6 机械手奇异位形Fig.6 Manipulator singular configuration

从图中可知，该机械手并无出现2个以上关节轴线的平行或垂直，即无内部奇异位形的出现；此位形只是机械手达到工作空间边界，属于边界奇异位形，远离工作空间边界或在奇异点附近对奇异位形进行处理，就可以避免．通过对求得的奇异位形进行分析，了解了四自由度机械手运动性能，为示教和轨迹规划提供可靠的依据[11]．

4 结论

1）通过应用旋量理论对四自由度机械手的运动学建模和速度雅克比矩阵求解，体现了旋量理论简洁、准确的特点．

2）结合互易积及反旋量相关理论，将求解逆雅克比矩阵问题转化为操作空间速度参数的线性关系问题，应用该方法对四自由度抓取机械手的奇异位形进行求解，经随机取点法验证表明，该方法准确可靠．

3）总结了奇异位形种类及危害，对四自由度机械手奇异位形进行分析，为控制系统避开这些奇异位形提供了重要的数据．

[1]CuiGenqun，LiChunshu，ZhangMinglu．Kinematic AnalysisofMobileManipulator forMeasurementand Maintenance in DangerousEnvironment [J]．JournalofWuhan University of Technology，2006，28（1）：983-988．

[2]RuggiuM．Kinematicsanalysisof the CUR translationalmanipulatormachine[J]．Mechanism and Machine Theory，2008，43（9）：1087-1098．

[3]Kanaan D，Wenger P，Chablat D．Kinematic analysisof a serial-parallelmachine to the VERNEmachine[J]．Mechanism and Machine Theory，2009，44（2）：487-498．

[4]张鹏程，张铁．基于矢量积法的六自由度工业机器人雅可比矩阵求解及奇异位形的分析 [J]．机械设计与制造，2011（8）：152-154．

[5]HU Zhun-qing，FANGHai-rong，FANG Yue-fa．Simulation Analysisof Low-DOFSerialManipulators[J]．Journalof System Simulation．2003，15（5）：693-695．

[6]李君．基于旋量理论的Stanford臂的运动学分析 [J]．天津科技大学学报，2010，25（4）：72-78．

[7]万海波．五自由度机械手运动性能及动力学分析与仿真 [D]．天津：河北工业大学，2007．

[8]路立军．旋量理论概述 [J]．机械工程师，2012（4）：39-42．

[9]杨扬．基于特种工件的大工作空间喷涂机器人设计与分析 [D]．北京：北京交通大学，2012．

[10]有伦．机器人技术基础 [M]．武汉：华中科技大学出版社，1996：78-81．

[11]李诚，谢志江，倪卫，等．六自由度装校机器人雅可比矩阵的建立及奇异性分析 [J]．中国机械工程，2012（23）：1165-1174．

[责任编辑 田 丰 夏红梅]

Analysison the singular configuration of 4-DOFholding manipulatorbased on the Screw Theory

LIU Qingsong，YUAN Jie，QIAN Jianhua

(China Nuclear Power Technology Research Institute,Guangdong Shenzhen 518124,China)

Thesingularconfigurationisoneofthemostsignificantfactorsthatinfluencesthekinematicsperformances ofmechanism.Itmay cause problems likemechanism lockup,control complicated,and the safety of staff endangered, etc.Thisarticleanalyzes4-DOFholdingmanipulator in kinematics referring to the Screw Theory and derives the singular configuration of themanipulator aswellas the feasibility of screw theory tested with the random pick-up-pointmethod. Based on this,itdoesa furthersimulation analysisabout the singular configuration using Matlab Robotics.The resultof the simulation analysis shows that the data drawn from Applicable Screw Theory is reliable and the data can effectively elim inate singularconfiguration phenomenon tomakesure themechanismmanipulatorcan complete capturing task quickly and accurately.

singularconfiguration;manipulator;ScrewTheory;randompick-up-pointmethods

TP242

A

1007-2373(2016)06-0031-05

10.14081/j.cnki.hgdxb.2016.01.006

2014-08-23

国家863计划（2011AA040201）

刘青松（1972-），男（汉族），高级工程师．

数字出版日期：2016-02-27数字出版网址：http：//www.cnki.net/kcms/detail/13.1208.T.20160227.1611.006.htm l