“几何画板”有效助力初中数学课堂深度教学
2021-01-19叶菊凤斌
叶菊 凤斌

摘要:几何画板的恰当使用,有助于发现知识间的逻辑关联,有助于概念的理解、比较、记忆,有助于提高思维的严密性与变化性,可有效助力课堂深度教学。
关键词:几何画板 初中数学 深度教学
深度教学,才能促进学生的深度学习,而学生深度学习,是促进学生数学核心素养落地的有效途径。几何画板一直是一种使用普遍的教学工具,它可以让作图更精确,其拖拽、数据监控等功能,可以培养学生思考的连续性,便于学生在变化过程中发现图形性质的不变性,发现其规律。几何画板的这些工具性作用,可以一步步将学生的思维引向深处,助力数学课堂深度教学。
一、几何画板使用的误区
几何画板动态演示功能非常好用,但其展示的只是形态,不能代替数学推理过程。有的教师“不究其理”,只关注表象,把其当作“动画片”放映。学生知其然,不知其所以然。这样的课堂看起来热热闹闹、精彩纷呈,实则学生是云里雾里、不明就里。学生的思维得不到训练,能力得不到提升,数学学习浮于表面。这样使用几何画板,完全没有发挥其优势,是“低层次”的使用。
很多几何题目编写过程,教师是借助了几何画板进行演示,发现结论,然后再反推回去,命制题目。有的老师在讲解习题时,也借助几何画板的功能,先发现其中的规律,再带着这种已有的认知解决问题。这种方式看上去非常巧妙,但是学生考试时是没有几何画板作为辅助工具的。如何从已知和问题出发,找到解决问题的方法呢?这种做法,导致学生跟不上教师的解题思维,解题目标不明确,解题方法突兀,解决问题的过程不顺畅,难以学到解题的方法。这样使用几何画板,颠倒了学生的认知顺序,打乱了学生的思考逻辑,几何画板沦为了教师“变戏法”的工具。
二、几何画板助力课堂深度教学的途径
(一)几何画板有助于发现知识间的逻辑关联
深度教学需要教师关注知识间的逻辑关联,准确把握知识内核,着眼于学生的最近发展区,创设适合深度学习的教学环节。
“线段的长短比较”这一节的内容主要有四部分:用叠合法比较线段的长短、线段的和差、线段的中点、一个基本事实(两点之间的所有连线中线段最短)。有老师发出疑问:“线段的长短比较”只是本节课的一部分内容,为何用它作课题呢?产生这种想法,其实是他把这四部分内容割裂开理解了。如果深入理解教材,会发现这四部分内容是个有机的整体,借助几何画板,可揭示其中的逻辑关联。
本节课的第一部分内容是用叠合法比较线段的长短,因为学生生活中有比较身高、比较小木棍的长短之类的实践经验,这部分内容对学生而言,并不深奥,只需要关注比较的规范性和表达方式即可。这部分内容是本节课的中心,后面的内容都是围绕它展开的。利用几何画板画一条线段AB,另取一动点C。动点C在线段AB上,可以探究线段长短与和差关系,明确线段的中点;动点C在直线AB外,可以助学生理解两点之间线段最短这一基本事实。
由此可见,本节的后三部分内容均是由“线段的长短比较”延伸出来的。如果不使用几何画板,教师要用很多时间画一张张静态的图;用几何画板让点C运动,真正将线段和点置于平面内,不仅找到了知识间的逻辑关系,还展示了数学研究的一般方法,激活了学生的思维,拓展了学生思维的广度和深度。
另外,用几何画板监控线段的长度,当点C运动时,每条线段的长度立即呈现出来,可迅速判断线段长度之间的关系,让学生的思考过程不会被细枝末节打断、打乱,可以将注意力集中在要研究的有价值的问题上,让整个的探究过程更加顺畅、自然,为学生的深度学习提供了保障。
(二)几何画板有助于概念的理解、比较、记忆
数学概念学习重在理解和应用,而不是浅层次的文字记忆。多角度、立体化地认知,可以加深学生对概念的理解。
数学教学中有时会遇到一节课出现非常多的小概念的情况,这些概念的内容并不一定需要一字不漏地背诵下来,但是需要准确地理解,会辨析,善应用。例如“圆”这节课,有很多与圆相关的概念,如弧、半圓、优弧、劣弧、弦、直径、弓形等。这些概念的介绍,会消耗很多时间,且不利于概念间的比较和记忆,若能找到它们间的联系,就可达到事半功倍的效果。这时我们就可以利用几何画板,让圆上的点动起来,通过演示点的运动过程,把这些琐碎的概念“串”起来,不是以“知识点”,而是以“知识串”的形式出现,在概念形成的同时,进行了概念的比较和辨析,省时又高效。变化的图形这种活泼的形式还会加深学生记忆,让学生有构建知识体系的意识,促进了学生的深度思考。
(三)几何画板有助于提高思维的严密性与变化性
几何画板的使用让课堂上数学思维的训练更便捷,尤其体现在分类讨论的思维训练和变式教学的应用上。
分类讨论体现了数学思维的严密性,是中学数学非常重要的思想方法,也是初中数学教学的难点。一些没有图形或者只有部分图象的几何题,由于条件的不确定性,在画图过程中会出现多种情况。但如果图像画的不够准确,就可能出现漏解的情况。
例1 已知△ABC,∠C=90°,若AB=10,
(1)求△ABC的面积。
(2)添什么条件,可求出△ABC的面积?
对于问题(1),由于题中△ABC形状不确定,故面积也不确定。点C的轨迹有何规律?教师可以引导学生在思考的基础上用几何画板展示,然后通过拖拽改变三角形形状,从而发现满足条件的△ABC有无数个,点C在以AB为直径的圆上。这样可以让学生更深刻地理解本题。
对于问题(2),学生一般都是添加一边长,或是间接给出一边长。如果添加斜边上的高,可以吗?学生先画图感知,但学生画的图可能不够精确,会影响最后判断。此时,几何画板精确作图的优势就发挥出来了。
用几何画板进行变式教学,更容易让学生把握问题的本质,发现解决此类问题的共性通法,为学生的深度学习提供平台。
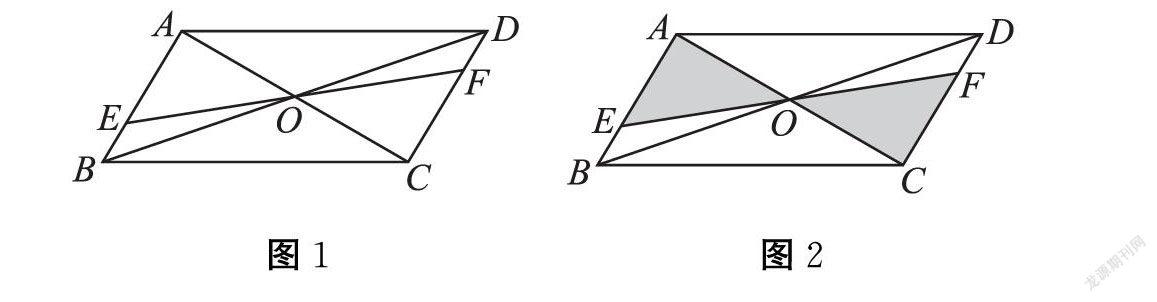
例2 已知:如图1,平行四边形ABCD的对角线AC、BD相交于点O,EF过点O,与AB、CD分别相交于点E、F,求证:OE=OF,AE=CF,BE=DF。
分析:本题可通过证明△AEO≌△CFO得到。
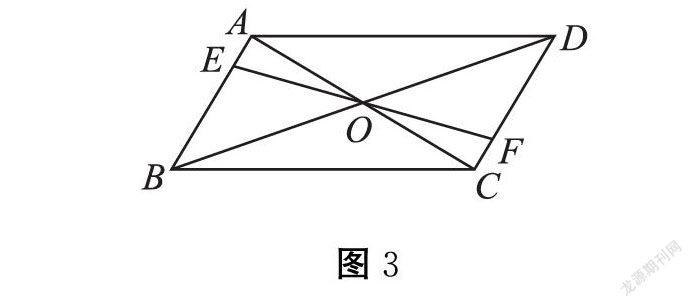
为引导学生发现问题本质,可以利用几何画板演示EF旋转过程。学生会发现在旋转过程中结论仍然成立。(图3)
动图演示,让学生体会EF还可能出现的位置。点E、F可能分别在边AD和BC上,直线EF还可能与平行四边形边的延长线相交。
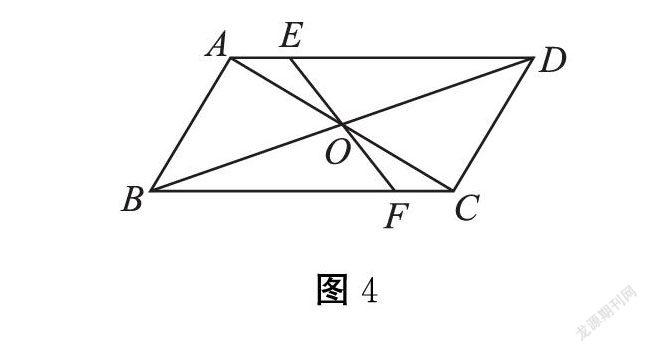
变式1:如图4,条件都不变,若点E、F分别在边AD、BC上,是否有相似的结论?
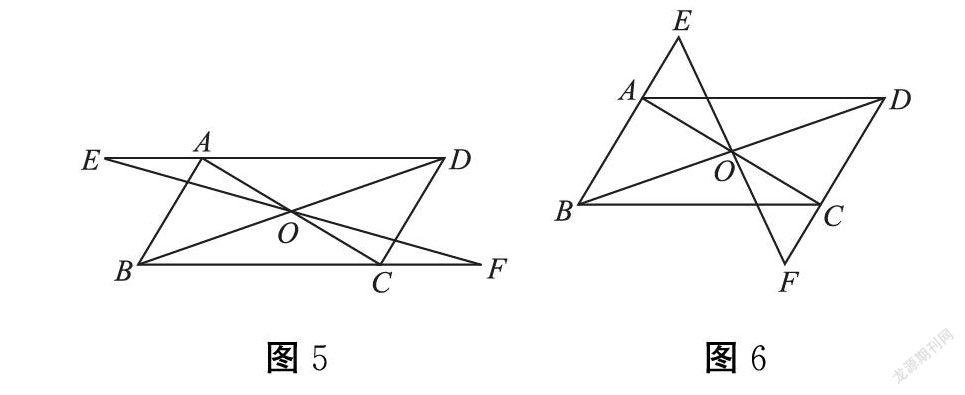
变式2:如图5、6,如果将EF向两端延长与平行四边形ABCD两对边的延长线分别相交,是否有相似的结论?
用几何画板演示EF旋转过程,学生的思维不会受某一种静态情况的禁锢,更容易发现变化过程中的不变性,找到解决这一类问题的共性通法。
几何画板的引入,让思维的过程可视化,探究的过程更有延续性,学生的思考过程更加完整,保障了探究式教学的流畅性,学生不断动手动脑、学思结合,思维能力得到了深度发展。
三、使用几何画板的注意事项
(一)思考在前,展示在后
深度教学需要让学生深度思考,几何画板是一种辅助工具,不能替代学生的思考过程,故要“滞后”使用,先给学生充分的探究、思考时间,再借助其进行验证、总结。
比如“圆的确定”这节课,先通过回顾,让学生明确,根据圆心和半径可以确定一个圆,再探究圆的确定的其他方法。
探究活动一:在平面内任取一点A,经过点A你能画几个圆?
探究活动二:在平面内任取两个点A、B,经过这两个点,你能画几个圆?
这两个探究活动,如果直接用几何画板展示,只需要2~3分钟就能解决,但是会毫无思维含量。所以,每个探究活动,都是让学生先思考,然后用圆规在草稿本上画图,再和同学交流。比如探究活动一,当学生发现过一点,可以画无数个圆后,教师再用几何画板展示画圆的过程:先确定圆心,圆心可以取除点A外的任意一点,圆心确定了,半径就随之确定了,因为圆心的位置有无数个,所以过点A的圆有无数个。探究活动二,在学生通过作图,发现过两点可以画无数个圆,这些圆的圆心在线段AB的垂直平分线上以后,教师再用几何画板展示、验证。
(二)恰如其分,谨防滥化
幾何画板虽优点多多,但只是优化课堂的手段,非必需品。教学也好,解题也罢,始终应该以学生为主体,以学生已有的知识储备、学习能力为基础,让新知自然生长,而不能被辅助工具牵着鼻子走。在一些合适的时机,恰当选用辅助工具,才能达到深度教学的效果。
深度学习属于高阶思维,几何画板可以将一些抽象的语言表达具体化地呈现出来,便于学生思考,教师使用几何画板时应该准确把握数学学科本质以及数学知识内核,淋漓尽致地发挥几何画板的优势,优化学习环境,在数学课堂上真正实现教师深度教学,学生深度学习。
参考文献:
[1]陈燕萍.用几何画板,教漂亮数学[J].中学数学参考,2021(17).
[2]袁丽华.例析几何画板在初中数学教学可视化中的应用[J].安徽教育科研,2021(11).
[3]杨静静.几何画板开展初中数学实验的教学研究[J].中小学电教,2021(4).
[4]郦兴江.数学思维异构让深度教学真正发生[J].中学数学教学参考(中旬),2020(3).
责任编辑:黄大灿
