让例题成为数学活动的素材

王强强

摘  要：数学基本活动经验的积累离不开数学活动，数学活动的开展必然以活动素材为依托. 文章将一道教材例题拓展为综合实践的活动素材，以学生的视角来预设活动场景，以学生自主探究来创设活动内容，充分挖掘出例题的教学价值与潜在功能，重视直观操作和逻辑推理的有机结合，让学生在探究的过程中获得丰富的数学活动经验.

关键词：例题教学;活动素材;活动经验

一、引言

《义务教育数学课程标准（2011年版）》明确提出，确定的目标有两类：一类是结果性目标;一类是过程性目标. 一般来说，结果性目标是指向基础知识与基本技能的. 过程性目标更多地指向数学基本思想和基本活动经验，而数学基本活动经验主要是过程性目标的体现. 这就意味着学生除了要掌握必要的数学知识和技能外，还要学会数学地思考，并在多样化的数学活动中积累经验.

接下来，就面临一个教学上的实际困难：开展数学活动所需要的素材从何而来？现行教材显然不大可能一一提供. 这就需要我们在教学实践中善于发现、敢于尝试.

下面是浙教版《义务教育教科书·数学》八年级下册（以下统称“教材”）“5.2菱形”（第2课时）的一道例题教学处理（如图1）. 研读教材时，发现教材是以“一张长方形纸片的折叠”作为“合作学习”，进而得出菱形判定的两个定理，那么我们是否仍然可以尝试通过“折叠”，对教材例题进行重组与改编，将例题转变为一个数学活动的素材，让学生在探究的过程中获得丰富的活动体验.

二、例题呈现

题目 （教材第122页例2）如图2，在矩形ABCD中，对角线AC的垂直平分线与边AD，BC分别交于点E，F.求证：四边形AFCE是菱形.

三、教学功能与价值分析

第一，例题为学生提供了一个利用“菱形的判定定理”进行合理论证的机会.明确“菱形”证明的基本套路：一是直接由“四边形”，经“四边相等”证明;二是遵循“从一般到特殊”的路径，由“四边形”先说明是“平行四边形”再说明是“菱形”.更进一步明确四边形、平行四边形、菱形的从属关系与逻辑结构;帮助学生加深对“四边形到一般平行四边形再到特殊平行四边形是一个从一般到特殊的过程”的理解与贯通，理清知识脉络.

第二，培养学生的逆向思维能力，为学生从不同角度，利用多种方法去探究指明了方向.从菱形“边”“对角线”的特性出发，去寻求证明思路，帮助学生深刻领悟其中所蕴涵的转化思想，即菱形向平行四边形、三角形转化的思想，从而丰富、积累获得数学活动经验的有效途径.

第三，“垂直平分线”为“折叠活动”的开展提供了操作的可能与良好的素材.例题中“AC的垂直平分线”完全可以与“对折操作”相匹配，实践中完全可以引导学生将两者进行很好地融通，被学生发现并应用于活动中.

第四，为多策略解决、多样化操作、多层次思维提供示范. 突破教材例题背景单一，打破例题文本描述的枯燥，形式上体现多样性与趣味性，加大可操作性与综合性，更大程度上去挖掘与提升例题的教学价值与功能.

四、教学实施

第1阶段：抛出问题——自主探索.

问题1：给你一张平行四边形纸片，你能作出一个菱形吗？说说你的做法與理由.

【设计意图】由于菱形是特殊的平行四边形，因此，笔者特意设计问题1，对学生的自身经验及其自主性学习给予更多地关注，旨在“动态”演示菱形的形成过程，明确菱形和平行四边形的构成关系，架构菱形（新识领域）与平行四边形（熟识领域）的逻辑关联，帮助学生进一步理解菱形与平行四边形的联系，“唤醒”学生的学习经验，营造问题情境，以激发学生的学习兴趣.

第2阶段：汇报交流——矫正互学.

要求学生回答并交流.教师进行追问、激励与评析，师生共同进行相互矫正与完善.

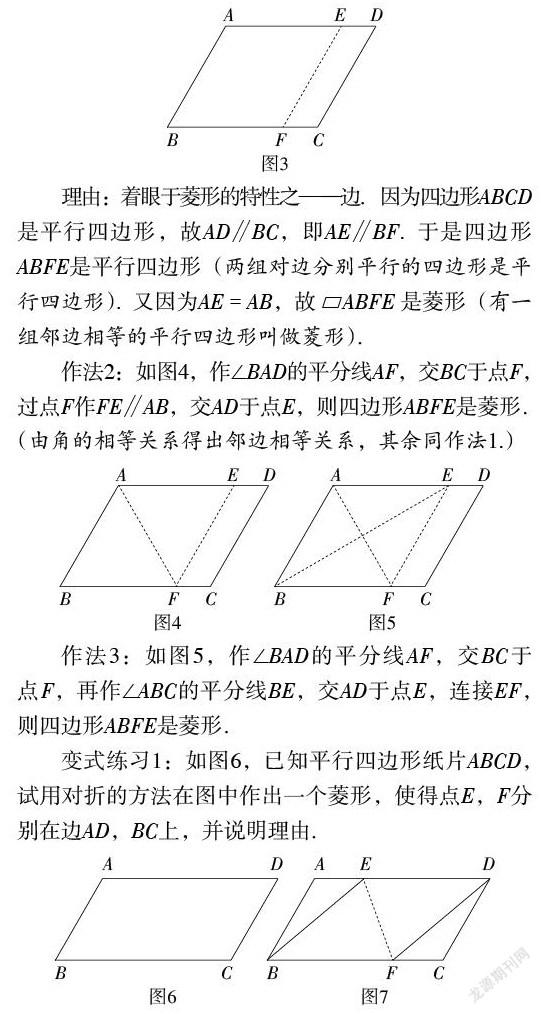
作法1：如图3，在AD上截取AE = AB，过点E作EF∥AB，交BC于点F，则四边形ABFE是菱形.

理由：着眼于菱形的特性之——边.因为四边形ABCD是平行四边形，故AD∥BC，即AE∥BF. 于是四边形ABFE是平行四边形（两组对边分别平行的四边形是平行四边形）. 又因为AE = AB，故[▱ABFE]是菱形（有一组邻边相等的平行四边形叫做菱形）.

作法2：如图4，作∠BAD的平分线AF，交BC于点F，过点F作FE∥AB，交AD于点E，则四边形ABFE是菱形.（由角的相等关系得出邻边相等关系，其余同作法1.）

作法3：如图5，作∠BAD的平分线AF，交BC于点F，再作∠ABC的平分线BE，交AD于点E，连接EF，则四边形ABFE是菱形.

变式练习1：如图6，已知平行四边形纸片ABCD，试用对折的方法在图中作出一个菱形，使得点E，F分别在边AD，BC上，并说明理由.

作法1：如图7，将[▱ABCD]沿某直线折叠使点B，D重合，折痕分别交AD，BC于点E，F，连接BE，DF，则四边形BEDF是菱形.

作法2：如图8，将[▱ABCD]沿某直线折叠使点A，C重合，折痕分别交AD，BC于点E，F，连接AF，CE，则四边形AECF是菱形.

【设计意图】变式练习1是依托“折纸活动”而设计的一道开放探究题.完全就是教材例题的另一个模版，尝试改变教材例题呆板的文字描述，试图从“探究”的角度去推动学生的学习进程，引导学生去分析、操作、发现. 同时，变式练习1是对学生逆向思维与推理能力的一个挑战，为学生从不同角度、用多种方法去探究指明了方向.

如何逆向思维呢？我们不妨适当还原学生的思维场景：（以图7为例）由于最终作出的四边形是BEDF，B，D两点已经确定，因此只要确定点E，F的位置即可. 如何确定点E与点F呢？因为四边形BEDF是菱形，不难发现BD是其中的一条对角线，EF必定是另一条对角线，那么如何确定另一条对角线EF呢？引导学生从菱形对角线特性的角度去寻求问题解决策略. 根据菱形特性，EF必然是BD的垂直平分线. 看到“垂直平分线”我们不难想到“折叠”，可以说“垂直平分线”为折叠探究活动的开展提供了操作的可能与良好的素材，“对折操作”完全可以与“垂直平分线”相匹配. 于是，通过逆向思维“作法1”很好地将两者进行融通. 使得不同作法的得出显得自然而然、水到渠成.

变式练习2：如图9，在[▱ABCD]中，点E在线段AB上，试在图中作出一个内接菱形EFGH，使得点F，G，H分别在边BC，CD，AD上，并说明理由.

作法：如图10，在DC上截取DG = BE，连接EG，作线段EG的垂直平分线，分别交AD，BC于点H，F，于是四边形EFGH就是所求作的菱形（理由略）.

【设计意图】提出数学活动经验，还有一个重要目的，就是培养学生在活动中从数学的角度进行思考，直观、合理地获得一些结果，提出猜想. 猜想：因为四边形EFGH是菱形，所以FH必然是EG的垂直平分线，于是只要确定点G的位置即可.如何确定点G呢？通过观察，大多数学生会想到“在DC上截取DG = BE”，教师用几何画板软件进行验证，发现猜想是正确的.这种基于理解的问题分析，恰恰是解决特殊四边形问题的基本套路，是逆向思维的理解与贯通，并为接下来菱形的证明提供了思考的方向.

接下来，如何验证是“菱形”呢？要作出的是一个菱形，借助以往的学习经验，大多数学生会从菱形的边或对角线这两方面入手.现在已知“FH⊥EG”，那么只需说明“四边形EFGH是平行四边形”即可.引导学生紧紧抓住“DG与BE之间的位置及数量关系”获得问题解决的多种策略. 使直观操作和逻辑推理有机地结合在一起，使推理证明成为学生观察、实验、探究得出结论的自然延续.

第3阶段：尝试运用——解决问题.

问题2：试折叠所给的矩形纸片，得到一个菱形，且使其四个顶点都在矩形的边上.

【设计意图】应该说“问题1”的解决为“问题2”提供了丰富的、可以借鉴的经验.从“平行四边形纸片”到“矩形纸片”创造性地使用素材（纸片），充分地挖掘出素材“差异”所带来的教学价值与潜在功能——一题多变、一题多用，帮助学生将零散的经验丰富化、条理化，让学生逐步地明确解决菱形问题的方法，实现了将知识向能力的转化.

作法1：（着眼于菱形的特性之——边）如图11，将矩形纸片ABCD对折两次，依次连接矩形四条边的中点E，F，G，H，则四边形EFGH即为菱形（理由略）.

作法2：（着眼于菱形的特性之——对角线）如图12，将矩形纸片ABCD沿EF折叠使点A，C重合，折痕EF交BC于点E、交AD于点F，连接AE，CF，四边形AECF即为菱形（理由略）.

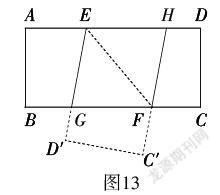
作法3：将矩形纸片ABCD沿任意线段EF折叠，如图13，得四边形[CDEF]. 使得[DE]交BC于点G，延长[CF]交AD于点H，四边形GEHF即为菱形（理由略）.

【设计意图】“作法2”巧妙地将“教材例题”蕴于其中，使得教材例题的呈现自然、简洁.“教材例题”只是作为活动中的一种形式，被学生发现并得以解决.“作法3”则是对“作法2”的进一步优化，是从特殊到一般的转化与提炼，更是对“教材例题”深入挖掘后的思维的“再认识”与“再提高”.

变式练习3：如图14，在矩形ABCD中，E为边BC上一点，且AE = CE.试仅用一把无刻度的直尺，画出一个以AE为边的菱形，并说明理由.

作法：如图15，第一步：连接AC，BD相交于点O;第二步：作射线EO交AD于点F，连接CF，则四边形AECF就是所求作的菱形（理由略）.

【设计意图】“变式练习3”创设学生主动运用已有知识解决新问题的情境，给学生更多自主学习、合作交流的机会，促进学生的主体参与，让学生在探究的过程中丰富活动经验.

五、教学反思

1. 以学生的学习视角预设活动场景，唤醒、激发学生的基本活动经验

设置问题1的目的之一是营造问题情境，激发学生主动学习的兴趣;其二，也是最主要的目的，是从学生的“现实知识基础”出发，唤醒学生已有的学习经验，引发学生思考，并促使学生在思考的过程中不断进行自我辨析、自我甄別、自我完善. 思考什么呢？一是要思考要作出菱形，首先要确保它是平行四边形，明确一般平行四边形与特殊平行四边形之间的从属关系与逻辑结构;二是要思考如何快速、准确地作出平行四边形，明确一般的平行四边形成立的标准（即平行四边形判定）;三是要思考具备怎样条件的平行四边形才是菱形，明确菱形作为特殊四边形所具有的特性（即菱形的判定）. 随着思考的深入，理性分析不断得到完善，问题解决的策略才会慢慢地清晰. 事实上，从学生作法当中，我们也深刻地感受到学生“冷静思维”带来作法上的不断创新、突破，紧紧围绕菱形“边”“对角线”的特性，特别是作法2、作法3，是学生通过自身的独立思考、相互交流、体验感悟，几何画板软件操作验证后的“集体智慧”的产物，可以说变式练习1的作法1、作法2（以及问题2的作法2）的得出已然完成“教材例题”所承载的教学功能.

问题1多样化、多角度动态演示菱形的形成过程，引导学生亲身体验、感知菱形与一般的平行四边形的图形特征差异，进一步明确菱形与平行四边形的构成关系，更好地呈现唤醒、激发学生基本活动经验等诸多学习过程，内化和发展学生的数学能力，提升学生的数学学科核心素养.

2. 以学生的自主探究创设活动素材，积累、发展学生的基本活动经验

问题2是对问题1的继承与拓展，渗透类比、转化、化归等数学思想，突出探究的过程，重视直观操作和逻辑推理的有机结合，使推理证明成为学生观察、实验、探究得出结论的自然延续，呈现积累、发展学生基本活动经验的活动过程，帮助学生将零散的经验丰富化、条理化，不单单是简单地完成对教材例题的解答，更是在问题解决的过程中，不断提炼方法、提升思维、打磨策略，形成有效化、多样化的活动经验与学科素养. 一是经验的迁移：学生运用问题1积累的学习经验即时解决问题2，