镍基高温合金高速超高速磨削成屑过程的三维仿真研究

2021-01-12丁文锋徐九华

金刚石与磨料磨具工程 2020年6期

夏江, 丁文锋, 仇博, 徐九华

(南京航空航天大学机电学院, 南京210016)

镍基高温合金由于具有强度高、耐高温、塑性韧性好、抗腐蚀性强等优势，已在航空、航天、舰船等领域得到越来越多的应用。与此同时，镍基高温合金优异的物理力学性能，也给其磨削加工带来困难，使其加工效率和精度降低、加工成本提高[1-2]。高速、超高速磨削加工作为一种高效磨削加工技术，其加工效率高，磨削力小，砂轮磨损少，能有效提高工件的表面质量，有助于改善难加工材料的可加工性[3-4]。

近年来，随着高速、超高速磨削技术的发展，国内外学者开展了许多高速、超高速磨削镍基高温合金材料的试验和研究工作，并取得了一定成果。JOHNSTONE[5]对Inconel 718镍基高温合金(类似于GH4169)进行了最大磨削速度为135 m/s的高速磨削试验，发现高速磨削在提高材料去除率的同时能降低磨削比能和工件表面温度。徐鹏[6]采用不同CBN砂轮在60～140 m/s速度下对GH4169镍基高温合金进行高速磨削试验，分析了磨削用量对其磨削力、磨削温度与比磨削能的影响规律。侯金涛[7]对高温合金开展磨削速度为90～150 m/s的高速磨削试验，研究了磨削工艺参数与其表面粗糙度的关系。尽管国内外学者对高温合金的高速磨削已经做了一些研究，但仍缺乏对其磨削成屑过程及成屑机制的研究，而这方面的研究有助于后续优化磨削工艺、控制磨削过程及改善磨削加工性能等[8]。

材料磨削过程实际上是大量磨粒同时与工件作用去除材料的过程，正因为磨粒数量多，影响磨削过程的因素复杂，从而对其进行准确分析比较困难。单颗磨粒磨削是对复杂磨削过程进行的简化，是了解磨削加工机理的一种行之有效的方法[9-11]。同时，高速、超高速磨削时的材料去除是在极短时间内发生的，磨削过程中磨削区域内的材料流动应力、塑性应变和温度等许多参数难以通过仪器实时且准确地观测；此外，许多试验研究都在150 m/s左右甚至以下速度进行，无法准确反映更高速度下高温合金的磨削加工情况，因而对超高速条件下的磨削研究较少。借助有限元仿真方法，可以有效模拟和再现高速磨削过程，反映单颗磨粒磨削时的材料去除和成屑过程[12-14]。因此，作者通过这一手段对更高速度下的高温合金磨削加工进行研究。

现在许多学者采用三维模型来进行磨削仿真研究，与二维模型相比，三维模型能建立更真实的磨粒模型，同时也考虑到了材料的侧向流动，能观察磨痕形貌和隆起特征等，因而更加直观、准确[9, 12, 15-16]。基于Abaqus软件对金刚石单颗磨粒磨削GH4169镍基高温合金的过程进行三维有限元仿真，研究其磨削成屑过程与成屑机制，讨论磨屑形貌及磨削力变化规律，探究应力、应变和温度等物理参量的分布和变化，分析磨削速度和单颗磨粒切厚对磨屑形貌、成屑频率及隆起情况的影响。

1 有限元模型建立

1.1 磨粒与工件材料模型

由于CBN磨粒彼此间形状差异大、不规则，而金刚石磨粒晶形较好且耐磨性高，所以单颗磨粒试验往往选用金刚石磨粒进行，以便控制磨粒位姿和刃型[17-18]。因此，仿真选取金刚石磨粒，工件为GH4169镍基高温合金，其材料物理属性见表1。

表1 磨粒与工件材料的物理属性[19]

材料的本构模型能反映材料形变过程中流动应力等的变化，而正确合适的本构模型，决定了仿真结果的准确性。高速、超高速磨削过程中，材料处于高应变、高应变率和高温等条件下，在磨屑形成时会产生应变强化、应变率强化和热软化等。J-C本构模型综合考虑了应变、应变率和温度等的变化因素，适合描述材料高应变率下的变形行为[20]。J-C本构模型可表示为：

(1)

J-C模型主要参数见表2。

表2 工件材料J-C模型主要参数[21]

切屑分离准则是有限元磨削仿真中判断切屑与工件基体是否分离的依据，本试验采用J-C损伤准则。它是基于单元积分点处的等效塑性应变的物理分离准则，当损伤参数D超过1时断裂发生。

(2)

(3)

表3 工件材料J-C损伤参数[22]

磨粒与工件的摩擦是磨削力的主要来源之一，摩擦产生的热量是导致磨削区域温度升高的重要因素。采用库仑摩擦定律，摩擦应力为：

(4)

式中：τf为摩擦应力；σn为接触面上的正应力；μ为摩擦系数，一般取0.1[23]；τs为材料的极限剪切应力。

1.2 单颗磨粒磨削有限元模型建立

单颗磨粒磨削时的磨屑厚度是不均匀的，图1为单颗磨粒磨削轨迹示意图。图1中单颗磨粒的最大切厚agmax是磨削过程中的关键要素，其表达式为[24]:

(a)单颗磨粒实际磨削轨迹Actual grinding track of single abrasive

(5)

式中：λ为有效磨粒平均间距，vw为工件进给速度，vs为磨削速度，ap为磨削深度，ds为砂轮直径。其中的磨削速度vs越大，磨削时材料的变形程度就更剧烈，进而也会对磨削过程产生影响。

图1a中单颗磨粒的磨削实际轨迹为圆弧，但由于磨粒的磨削深度远小于砂轮半径，从而单颗磨粒的切厚远小于磨削弧长，因而可将其视为图1b的直线运动。从磨削速度vs和单颗磨粒切厚agmax2个参数出发，分别进行改变磨削速度或单颗磨粒切厚条件下的2组单颗磨粒磨削仿真，探究其对磨屑形貌的影响规律。具体磨削仿真工艺参数见表4，其涵盖了高速磨削与超高速磨削时的工艺参数。

表4 单颗磨粒磨削仿真工艺参数

仿真中的磨粒采用代号40/45(平均粒径为420 μm)的金刚石磨粒，金刚石磨粒及其仿真模型如图2所示。从图2a可以看出：金刚石磨粒的表面形貌并不完全一致，不同金刚石磨粒的形状和尺寸都有差异，但也有一定规律性，其表面多为四边形与六边形。目前，诸多仿真研究都对金刚石磨粒进行简化，简化为圆锥体、球体、多棱锥体、截角八面体等。本试验采用截角八面体来对金刚石磨粒进行模拟[9]，其形状与实际磨粒形状更接近，磨粒尺寸为355～425 μm，关键边长尺寸a=104 μm，如图2b所示。

(a)金刚石磨粒Diamond abrasive

图3为单颗磨粒磨削仿真有限元模型，图中的工件尺寸为50 μm×60 μm×15 μm。由于金刚石磨粒的硬度和强度远大于GH4169镍基高温合金，且磨削中变形小，可不考虑其磨损与变形，将其定义为刚体。考虑到实际单颗磨粒磨削中，单颗磨粒的最大切厚agmax远小于磨削深度ap(图1a)，截取磨粒参与磨削的区域进行仿真以缩减计算量(图3a)，保留磨粒侧刃以便仿真观察材料的侧向流动。同时，因为磨粒与工件都具有一定对称性，取对称的一半仿真来节省计算时间。仿真中，磨粒前角为-45°(α=45°)，并给予一定后角(β=10°)；磨粒与工件相互接触的区域网格尺寸细化(图3b)。考虑到仿真的一致性以及结果的准确性，不同参数下磨粒和工件的网格保持不变。图3的工件单元数为1 500 000，磨粒单元数为110 711。

(a)仿真磨削示意图Schematic diagram of simulation grinding

此外，实际磨削中工件进给速度远小于砂轮线速度，因此仿真中可以将工件固定不动，对工件底部施加固定约束，同时在工件对称面施加对称约束。另外，限制磨粒在其他方向上的自由度，磨粒只沿磨削方向保持一定速度运动。

2 仿真结果与分析

2.1 磨屑与工件表面形貌仿真及试验

为了方便观察，对仿真结果中的磨粒进行隐藏，仿真得到的单颗磨粒磨削GH4169的磨屑和工件表面形貌如图4所示。

从图4a可以看出：工件整体形貌中的工件材料受磨粒挤压，在磨粒前面和侧面形成隆起，之后随着磨粒切入，大量材料沿前刀面流出，形成磨屑，同时侧面的隆起也发展成毛刺和飞边。图4b的磨屑与磨粒接触面比较平整，没有大的凸起。图4c的磨屑与磨粒的接触反面(即磨屑自由表面)则出现一些平行的条纹状凸起，与磨屑流出方向基本垂直。图4d和图4e分别为平行与垂直于磨粒运动方向的XY面和XZ面工件截面图，从图4d和图4e中可直观看到磨屑的侧面形态、磨痕深度与其侧面隆起等情况。如图4d所示：磨屑侧面一侧为直线，另一侧呈现锯齿形状，这与图4b、图4c中的磨屑情况吻合。如图4e所示：磨粒侧面的工件材料受到磨粒的挤压产生了一定的隆起，这在整个已加工表面则表现为毛刺，会降低已加工表面的质量，在磨削过程中应当抑制该现象发生。

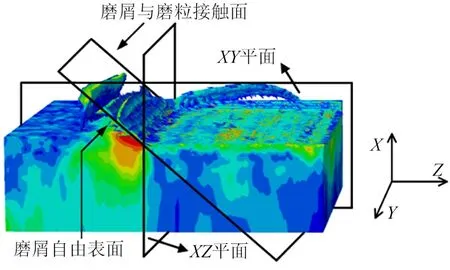
(a)整体形貌Overall topography

在高速、超高速磨削过程中，磨粒与工件会在极短时间内相互作用产生大量的热，由于接触区域处于绝热状态，热量来不及传出；同时，因磨粒一般为负前角，加工时加剧材料变形，产生更多热量，更容易发生绝热剪切，形成锯齿形磨屑，如图5所示，其剪切滑移特征如图5a所示。

(a)锯齿形磨屑模型示意图Schematic diagram of sawtooth chip model

由于镍基高温合金热导率低、高温下仍有较高强度等特点，磨削时绝热水平更高，更容易出现塑性失稳，产生集中剪切滑移。图5b为仿真得到的磨屑形貌，该形貌符合绝热剪切特征，即出现了很明显的锯齿形磨屑。

为验证仿真得到的上述磨屑形貌，开展vs=40～200 m/s，agmax=1 μm时的GH4169磨削试验。图6为试验工艺参数vs=80 m/s，agmax=1 μm时的磨屑形貌。

(a)磨屑与磨粒接触面Contact surface between chip and abrasive

从图6中可以看出：磨屑与磨粒接触面处的形貌与仿真得到的类似(图6a和图4b)，其整体平整，有许多褶皱，但起伏不大，这是磨削时出现集中剪切滑移，裂纹向磨屑底部延伸的特征(图5a)；磨屑自由表面沿磨屑流出方向整体呈片层结构，存在许多与磨屑流出方向垂直的条纹，其剪切滑移面比较光滑，这些特征也与仿真结果类似(图6b和图4c)。因此，仿真能一定程度上真实反映磨削中磨屑的形成过程以及磨屑形貌的变化。

2.2 磨屑形成过程与磨削力

单颗磨粒切厚为1 μm、磨削速度为200 m/s时的磨屑形成过程中的磨削力变化如图7所示，其中图7a、图7b分别表示整个磨削过程中磨削力的变化和1个周期内(图7a中的方块C区域)的磨削力变化。图7a中：磨粒与工件刚开始接触时，磨粒切厚增大，产生冲击载荷，导致磨削力急剧升高，达到0.90 N；之后单颗磨粒切厚保持一致，进入稳定磨削阶段，磨削力下降，但同时随磨削进行呈周期性变化，单颗磨粒磨削力在0.50 N左右波动；之后磨粒前刀面离开工件，其受到的阻力降低，磨削力减小，但磨粒后刀面和侧刃仍继续与工件接触摩擦产生磨削力，直到磨粒后刀面和侧刃完全离开工件，磨削力才变为0。

(a)整个磨削过程中磨削力的变化Changes of grinding force in the whole grinding process

由于图5中的磨屑呈锯齿形状且具有周期性，是由许多锯齿节块连续组成的。因此，取图7b的一个周期内的磨削力波形图上的1～6点，得到其各时间节点对应的磨屑形貌如图8所示。从图7b和图8可以发现：1个锯齿形节块的形成时间十分短暂，不到0.03 μs，因此材料在极短时间里发生剧烈变形。在第1点处，磨削力最小，为0.37 N，第3个锯齿节块基本形成，磨粒开始与新的工件区域接触，工件出现隆起；时间延长，与前刀面接触面积增大，磨削力不断增大；在第3点磨削力达到峰值，磨削力为0.70 N；再后，材料开始出现塑性失稳，主变形区开始集中剪切滑移，磨削力下降；而在第4点和第5点之间磨削力下降速度变缓，磨削力在0.45 N上下波动。从磨屑形成的形貌上看，主要是因为磨屑自由表面韧性断裂需要能量，进而导致磨削力变化不大甚至短暂升高；自由表面区域出现断裂后，剪切滑移程度加剧，磨削力很快降到谷底，第4个锯齿节块基本形成；第6点处磨削力为0.37 N，与第1点的磨削力大小一致，磨屑形成过程的1个周期结束。由此可见，磨削力的周期性变化与磨屑锯齿节块的形成相互对应，工件材料受挤压隆起时，磨削力增大，剪切滑移出现后，磨削力下降。

2.3 应力、应变、应变率及温度的分布与变化

磨屑形成呈连续周期变化，可以选取其中1个磨屑节块形成过程进行分析。图9为单颗磨粒切厚为1 μm、磨削速度为200 m/s时磨屑节块剪切滑移阶段的应力、应变、应变率及温度分布情况。

从图9a可以看出：磨削区的高温部分主要集中在磨刃附近和剪切带区域，最高温度可达到1 000 ℃以上。这是因为这些区域的材料等效塑性应变较大(图9b)，材料变形也较大，进而产生的塑性变形功较多，由其转化的热增多，所以温度也就较高。同时，由于材料热导率较差，加之磨削过程十分短暂，产生的大量热聚集在这些区域来不及传出，导致温度迅速升高，形成热软化区，产生热塑性失稳，发生剪切滑移。在剪切带区域，靠近磨刃处应变和温度更高，最先出现剪切滑移；而靠近工件表面处，应变和温度较中间区域大，随着剪切滑移的继续，区域内的材料塑性应变会增大至断裂标准后发生断裂，进而加剧第一变形区的集中滑移，最终形成锯齿形磨屑。从图9c可知：应力集中在剪切带两侧，而剪切带区域的流动应力小，这有助于材料剪切滑移的进行。图9d反映了等效应变率在剪切带两端(即靠近磨刃处与靠近工件表面区域处)升高，达到3×102(μs)-1左右，且有相互延伸趋势。

如图8a所示，从工件待加工表面向下取4个不同深度的单元(h=0.2、0.6、1.0和1.4 μm)为采样点进行追踪，得到其在磨削时的温度、等效塑性应变、等效流动应力及等效应变率随时间变化的情况图10。

如图10a和图10b所示：工件不同深度处的温度变化与其等效塑性应变的变化趋势基本一致，进一步说明温度与塑性应变密切相关。在0.126 0 μs时，磨粒与采样点位置材料接触，0.2 μm和0.6 μm深度处单元温度和等效塑性应变迅速上升，0.147 0 μs时就基本达到其最大值；而1.0 μm和1.4 μm深度处单元到0.143 0 μs时温度和等效塑性应变才开始大幅升高，在0.164 0 μs时达到其峰值。

如图10c所示：随时间延长，工件不同深度下的等效流动应力依次缓慢升高达到最大值，且最大值都比较接近，在1 850 MPa附近。时间继续延长，0.2 μm深度时的流动应力快速下降，1.4 μm深度时的流动应力剧烈波动，最后稳定在1 248 MPa(图10c中的细水平线)。但在0.6 μm和1.0 μm深度，根据前面的断裂准则，该处在成屑过程中网格失效，应力为0。

与此同时，磨削结束后，1.4 μm深度处的温度为129.6 ℃，等效塑性应变为0.256，说明已加工表面工件内部有塑性变形层和热影响区；其磨削后残余应力为1 248 MPa，高于前面表2中的材料屈服应力1 241 MPa，说明存在加工硬化过程[25]。

从图10d中可以看出：随时间增加，磨削深度0.2、0.6和1.0 μm处的等效应变率依次达到最大值，其中0.6 μm单元的最大应变率达到1.2×103(μs)-1，0.2 μm和1.0 μm处单元的等效应变率变化趋势相似，最大应变率可达2.1×102(μs)-1。1.4 μm处单元由于不在磨削区(材料的最大去除深度为1 μm)，因此等效应变率较低。由此可见，磨削尤其是高速磨削中材料去除过程是在极高应变率下发生的。

由图9和图10还可知：磨削区的不同深度是产生上述不同规律的主要原因。温度和等效塑性应变是从磨刃区域沿剪切带延伸分布的(图9a和图9b)，因而同一位置的表层材料(0.2 μm处)更早发生塑性变形且温度升高；同时，越靠近磨刃处，材料变形越大，温度和等效塑性应变就越高，因此图10a和图10b中的1.0 μm处的温度和等效塑性应变最高，分别为1 120.6 ℃和4.144。0.6 μm处由于处于剪切带的中心，变形程度大，变形速率快，因此温度、等效塑性应变和等效应变率也都很高；由于1.4 μm处位于已加工表面上(磨削结束后距离加工表面0.4 μm)，因此温度和等效塑性应变较小，但磨削结束后的流动应力较大，存在加工硬化现象。

2.4 磨削速度对磨屑形貌的影响

单颗磨粒切厚为1 μm时不同磨削速度下的磨屑截面如图11所示，图中所有的磨粒磨削距离相同。

从图11中可以看出：总体上随磨削速度增大，磨屑形貌由连续型锯齿状向锯齿分节分离的单元节状转变，最后发展成不规则带状断续磨屑。在磨削速度80 m/s时，磨屑自由表面就存在锯齿形特征，而在80～240 m/s时，磨屑形态均表现为连续的锯齿状；随着磨削速度进一步增大，锯齿间距变小，锯齿化程度增大；到400 m/s时，锯齿节块开始出现分离，随后变为单元节状磨屑。随着磨削速度继续增大，在600 m/s时磨屑形貌开始由锯齿状转变为带状，磨屑变得细长。磨削速度达到1 000 m/s后，磨屑已经转变为带状磨屑。

原因是磨屑的形成过程是工件材料在前刀面堆积，形成隆起，之后剪切带材料在绝热条件下剧烈变形，产生剪切滑移，而形成锯齿状磨屑。磨削速度越大，材料变形就越大，加剧剪切滑移的发生；但随着磨削速度进一步增大，在绝热环境下，大量热能聚集在磨刃周围的材料上，瞬间的高温导致其形成准流动相甚至流动相，材料流动加强，变形反而减小，许多工件材料甚至来不及发生变形就被去除，因而产生塑性流动，形成了细长的带状磨屑。磨削速度1 000 m/s时的仿真结果，就是明显磨屑材料自由表面基本没有变形，而形成了细长带状磨屑的典型例子。

从以上试验已知，磨削力的周期性变化与锯齿节块的形成相互对应，因而可以从磨削力曲线中得到磨屑锯齿节块的形成频率f。图12为磨削力信号及磨屑节块形成频率随磨削速度变化的规律，其中图12a是磨削速度为160 m/s、切厚为1 μm时的图像。

(a)磨削力信号Grinding force signal

如图12a所示：T为磨削力曲线中几个波谷间的一段时间，即取样时间；t1为一个波谷到下一个波谷之间的时间；n为取样时间T内的波峰数。在磨削过程中t1的大小并不恒定，为了能准确反映成屑情况，取样时间应尽可能长，且处于稳定磨削阶段，因而形成频率f可表示为f=n/T(n≥3)。而当磨削速度达到600 m/s时，由于磨屑转变为不规则带状(图11e)，磨屑节块形成频率f不再适合对磨屑形态进行表征。

如图12b所示：磨削速度为80 m/s时磨屑单元形成频率仿真结果为15.6 MHz，400 m/s时则达到了76.2 MHz；随着磨削速度增大，磨屑形成频率呈线性增大趋势。可见磨削速度增大会使材料变形更剧烈，剪切频率变大。同时，单颗磨粒磨削GH4169试验与仿真得到的磨屑单元形成频率能较好地吻合，在磨削速度为120～160 m/s时其相对误差不超过15%，进一步证明了仿真模型的可靠性[26]。

图13为磨削沟痕隆起随磨削速度的变化规律，通过测量图13a中隆起部分的截面积S1和沟痕部分的截面积S2，计算隆起比Rs=S1/S2值，来评价磨削表面的隆起情况。图13b中：磨削速度从80 m/s增大到1 000 m/s时，隆起截面积从1.27 μm2增加至3.93 μm2，隆起比从0.066增加到0.237，说明沟痕两侧隆起随磨削速度的增大而增大。主要原因是磨削等效应变率高，可达102～103(μs)-1(图10d)，极短时间内塑性变形产生的热无法传出，热软化作用使材料发生塑性流动，而速度越高热软化作用就越强，使沟痕两侧隆起面积增大；此外，因为单颗磨粒切厚保持不变，图13b中的沟槽截面积无明显变化。

(a)沟痕隆起截面示意图Schematic diagram of groove uplift section

2.5单颗磨粒切厚对磨屑形貌的影响

磨粒磨削相同距离且磨削速度为200 m/s时，不同单颗磨粒切厚下的磨屑形貌变化如图14所示。

图14中：单颗磨粒切厚为0.2 μm时，磨粒前方出现微小隆起，无磨屑出现，磨削还处于划擦耕犁阶段；而到0.3 μm时，材料在磨粒前端堆积，隆起加剧，开始出现少量磨屑；到0.5 μm时，碎状磨屑增多，磨削开始进入磨削成屑阶段；在0.8 μm处，可以看到锯齿状磨屑出现，但锯齿状磨屑较小且不显著；之后随着单颗磨粒切厚增大到1.0 μm和1.5 μm，锯齿状磨屑越明显，材料剪切变形也更剧烈。所以，从磨屑形貌变化上看，0.3～0.5 μm切厚为磨削开始成屑阶段。因此，磨削速度为200 m/s时，磨削高温合金GH4169的临界成屑切厚约为0.3 μm。

图15为不同切厚下单颗磨粒的法向磨削力及磨屑节块形成频率。通过计算图15a的磨削力波动周期得出磨屑节块的形成频率。

(a)不同切厚时单颗磨粒的法向磨削力信号Normal grinding force signal of single abrasive with differentcutting thickness

如图15b所示：单颗磨粒切厚在0.3 μm之前时，磨削还未成屑，因而磨屑单元形成频率f未予分析；单颗磨粒切厚为0.3～0.5 μm时，磨屑呈碎屑状，磨屑节块单元形成时间短，形成频率高，为53.0 MHz；在0.8 μm处磨屑出现锯齿化特征，磨削力呈周期性变化，节块形成频率下降，为45.7 MHz；单颗磨粒切厚继续增大，在1.5 μm时节块形成频率为31.8 MHz。可见随单颗磨粒切厚增大，磨屑单元的形成频率下降，但磨削力幅值变大[27]。

单颗磨粒切厚会对磨削沟痕隆起产生影响，如图16所示。图16中：单颗磨粒切厚为0.2 μm时，沟槽截面积几乎为0，几乎不存在沟痕隆起；单颗磨粒切厚从0.3 μm增大到1.5 μm过程中，沟痕隆起截面积从0.23 μm2增加至2.75 μm2，沟槽截面积从2.15 μm2增加至29.49 μm2。而隆起比则在切厚0.3～0.8 μm时，从0.11快速下降到0.04，这表明单颗磨粒切厚大于0.3 μm时，磨削加工从耕犁往成屑阶段过渡，大部分工件材料成为磨屑；单颗磨粒切厚从0.8 μm变化到1.2 μm时，隆起比又升至0.10，这主要是因为单颗磨粒切厚越大，磨削区域温度越高，热软化作用也越强所致；当单颗磨粒切厚从1.2 μm增加到1.5 μm时，隆起比略有下降。这是由于材料热导率低，切厚增大后表层材料的温度反而下降，不利于材料的塑性流动。图16b的θ1为50°，θ2为40°，θ1>θ2，即单颗磨粒切厚为1.2 μm时的材料隆起高于1.5 μm时的。