磨屑对TC4钛合金微动磨损行为的影响
2022-10-11王剑飞薛伟海高禩洋赵智超段德莉
王剑飞, 薛伟海*, 高禩洋, 赵智超, 段德莉, 李 曙
(1. 中国科学院金属研究所 辽宁省航发材料摩擦学重点实验室, 辽宁 沈阳 110016;2. 中国科学技术大学 材料科学与工程学院, 辽宁 沈阳 110016)
微动磨损是指两固体接触面上因出现周期性小振幅振动造成损伤的一种特有的磨损方式[1-3]. 微动形式主要分为切向微动、径向微动、扭动微动以及转动微动四种[4],其中,切向微动最为常见[5-6]. 钛合金由于其具有优良的性能,广泛用于制作航空发动机压气机和风扇的叶片[7]. 随着航空发动机高速运转,叶片的振动不可避免,而这个振动会导致叶片根部的榫槽连接处和相邻叶片的减振凸肩搭接处发生小振幅的相对运动,也就是切向微动磨损[8-9]. 微动现象的存在会造成接触面的磨损,引起结构间发生松动或破坏,也会加速疲劳裂纹的萌生和扩展,严重削减构件的疲劳寿命[9],甚至会带来灾难性的后果. 因此,研究钛合金间的微动磨损,具有重要的应用价值[10-11].
微动磨损相比于普通的滑动磨损,最重要的特点就是位移小,而小位移会导致微动磨损产生的磨屑难以排出,磨屑又以第三体的形式参与磨损[12-14]. 磨屑在微动磨损中既可能充当磨粒,加剧磨损,也可能黏附在接触面上形成氧化物薄膜,而这层薄膜能够在接触面上剪切和变形,从而缓冲接触面之间的相对滑动[15-16].因此,针对不同的磨损机制,磨屑对微动磨损的影响也不尽相同:如果是磨粒磨损占主导,磨屑的存在会促进磨损;如果是黏着磨损占主导,磨屑提供的抗黏着作用会大于其造成的磨粒磨损的影响,磨屑的存在会抑制磨损[17].
但是,在试验过程中无法实时观察到磨屑的演变[18],因此,磨屑对微动磨损影响的研究难度较大. 近年来,多数学者采用有限元方法研究磨屑对微动磨损的作用. Ding等[19-20]提出了微动磨损过程中可塑性演变的磨屑模型,并且和实测的磨屑厚度进行了比较. 研究表明,预测的磨屑层达到饱和时的厚度和相应微动循环周次随接触点的位置以及局部微动条件而发生变化. Arnaud等[21]通过改变第三体磨屑层的弹性性能,研究磨屑对磨损的影响. 结果表明,即使是弹性性能改善400%,对磨损深度的影响也仅为3%. Done等[18]对比了考虑磨屑和不考虑磨屑的数值模拟,然后与实际微动磨损试验结果对照,研究显示,考虑磨屑比不考虑磨屑更符合实际,对数值模拟而言,不考虑磨屑,磨痕深度更浅.
然而,有限元模拟只能得到一定微动周次后的接触区域的压力分布以及磨痕深度,无法给出一些反映微动磨损过程的信息,比如微动循环图(摩擦力-位移曲线)和磨屑的演化过程等,而微动循环图及磨屑的演化是反映微动磨损过程中动态信息的1个重要形式[22-24]. 通过微动循环图能直观得出施加位移和滑移位移,两者之差即被定义为系统形变量(System deformation)[25],研究施加位移、滑移位移以及系统形变量之间的关系,具有重要意义. Fourvry等[26]定义了滑动率(Sliding ratio,D),即滑移位移与施加位移之比,并且通过理论推导得出D=0.26,将部分滑移区与滑移区划分开. Wang等[25]通过研究载荷、施加位移以及系统形变量的关系,发现了当施加位移一定时,滑移区的系统形变量与载荷存在线性关系,进而借助这个线性关系,提出了1个Ti-6Al-4V的球-平面接触微动磨损运行区域的预判公式,γ =(3.337+0.360×Fz)/Δ∗,其中,γ表示系统形变量,Fz表 示载荷,Δ∗表示施加位移. 根据设置的载荷和施加位移,代入到上述公式中,计算出γ ,如果γ <0.9,微动磨损则处于滑移区.
综上所述,目前对微动磨损中磨屑的研究大多侧重在对磨损的影响上,且多是运用有限元模拟的结果,对微动磨损中更为重要的微动循环图、摩擦系数和系统形变量的研究仍然不足. 在实际微动磨损的工况中,磨屑的存在及其给微动磨损带来的影响不可忽略. 因此,研究微动磨损过程中磨屑的行为机制,对深入理解微动磨损具有重要的理论意义. 在本研究中,通过设计中间清除磨屑试验,从减少磨屑的角度,探究在微动磨损过程中,磨屑对微动磨损的影响. 另外,又设计了表面织构储存磨屑的试验,从增加磨屑的角度,进一步佐证磨屑的影响.
1 试验部分
1.1 试验设备及试验材料
试验设备为Rtec微动试验机,其示意图如图1所示. 在左右两个大推力高频电磁驱动器的推动下,上梁带动上试样左右高频往复运动,同时,梁的上方为加载装置,提供法向载荷. 往复位移监测采用分辨率为0.1 μm的LVDT传感器,两个压电陶瓷传感器分别测量试验过程中的切向力(Fx) 和法向力(Fz).
此试验采用球-平面的接触形式,上球和下平面试样材料均为退火状态的TC4钛合金. 球的直径为10 mm,下试样为直径24 mm、高8 mm的扁平圆柱. 由于单次试验磨出来的磨痕极小,做完单次试验之后,将下试样旋转一定的角度,便可在上1个试验的磨痕附近进行第二次试验,因此,1个下试样表面至少可以做10次试验(图2).
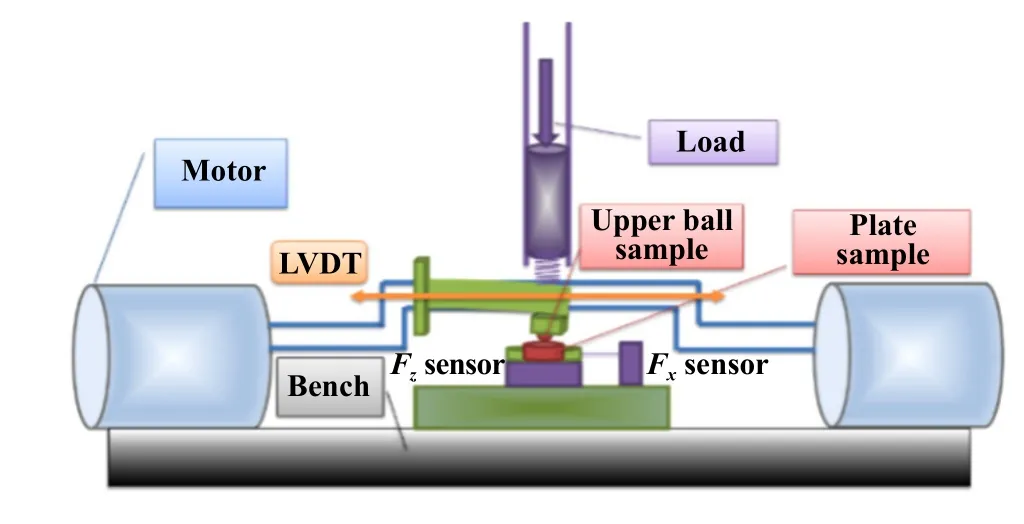
Fig. 1 Schematic diagram of Rtec fretting machine图1 Rtec微动试验机示意图

Fig. 2 Graphs of upper and lower samples after the test图2 试验后的上下试样照片
为了研究更多磨屑对微动磨损的影响,在钛合金表面制备沟槽状的表面织构,用于捕获磨屑. 表面织构用激光来加工,制备完成之后,使用砂纸打磨掉表面飞溅的熔滴. 使用KEYENCE VHX-6000光学显微镜对表面织构进行观察,其三维形貌结构如图3所示.
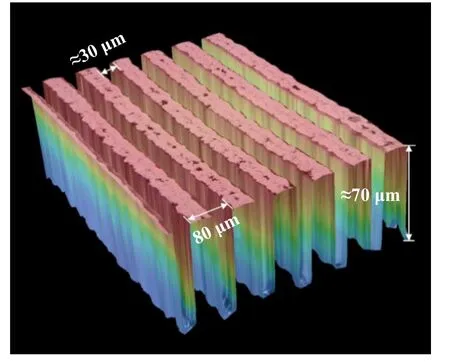
Fig. 3 3D topography of the surface texture图3 表面织构的三维形貌
1.2 试验过程
试验前,先依次用砂纸打磨下试样,随后用SiO2抛光液抛光10 min,最后放入无水乙醇中用超声波清洗15 min. 样品准备好后,在室温下进行微动磨损试验,试验参数列于表1中(施加位移50 μm时,增加载荷为110和120 N的测试). 在每次试验中,微动磨损达到8万周次后,暂停试验,用干净的抛光布轻轻擦拭上试样和下试样,清除粘附于样品磨损区域的磨屑. 在擦拭的过程中,下试样保持不动,保证清除磨屑前后上下试样接触并发生磨损的部位不变. 清除磨屑之后,继续微动磨损2万周次. 试验结束后,在前8万周次内分别选取第4 500、14 500、24 500、34 500、44 500、54 500、64 500和74 500周次作出微动循环图,在后2万周次内分别选取第81 500、82 500、83 500、84 500、86 500、89 500、94 500和99 500周次作出微动循环图,然后再根据微动循环图计算系统形变量.
在有表面织构的试样上,仅选择在载荷为20、40和60 N,施加位移为40 μm条件下进行微动磨损试验,微动运行10万周次. 试验结束后,同样记录摩擦系数和系统形变量.
1.3 系统形变量的介绍
微动循环图能实时反映微动磨损过程中摩擦力与位移的变化,是研究微动磨损的1个重要手段. 而通过微动循环图,可以定义系统形变量[25,27]. 如图4所示,Δ∗表 示试验设置的施加位移,δ∗表示上下试样之间实际滑移的位移,S表示斜边的斜率,同时也是系统的刚度. 系统形变量(δs)则被定义为施加位移与滑移位移之差,即

换言之,施加位移(Δ∗) 由两部分组成:滑移位移(δ∗)和系统形变量(δs).
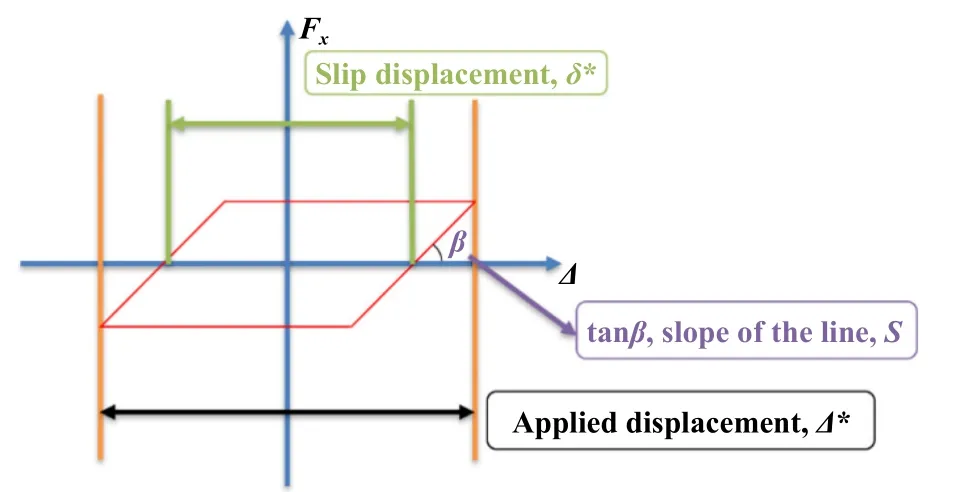
Fig. 4 Schematic diagram of the three parameters in the fretting loop[8]图4 微动循环图中3个参数的示意图[8]
系统形变量的物理意义为反映微动磨损的系统(摩擦对偶以及之间的磨屑层)在这个微动循环里面的变形程度,也可以理解为吸收部分施加位移从而减少滑移的能力. 比如,从公式(1)可以看出,当施加位移一定时,系统形变量的增大就意味着滑移位移的减小,因此,黏着区域增大. 换言之,系统形变量可以在一定程度上反映微动磨损中的滑移和黏着的关系,也就是能够反映出微动磨损中滑移区和部分滑移区所占比例. 在本研究中,摩擦对偶材料没有改变,通过暂停试验清除磨屑来改变磨屑层的厚度,制备织构捕获磨屑,从而探究磨屑对微动磨损过程的影响.
2 结果与讨论
2.1 清除磨屑对微动循环图的影响
从微动循环图的形状可以对微动运行区域进行划分:当微动循环图是直线或者是近似直线的椭圆时,微动磨损处于部分滑移区;当微动循环图是平行四边形时,微动磨损处于滑移区[28]. 因此,在本试验中,当20 μm施加位移下载荷大于等于40 N、30 μm施加位移下载荷大于等于60 N、40 μm施加位移下载荷大于等于90 N以及50 μm施加位移下载荷大于等于110 N时,微动磨损处于部分滑移区[24].
图5所示为在30和 50 μm施加位移下,清除磨屑前后的微动循环图. 从图5可知,无论是在30 μm还是在50 μm的施加位移下,微动循环图在清除磨屑的前后均有较大的变化. 具体表现为在30 μm位移下,当载荷为30 N时,清除磨屑后的摩擦力会显著下降,从而导致微动循环图由之前的“高瘦”状的平行四边形变成“矮胖”状的平行四边形;当载荷为60和90 N时,清除磨屑后最大摩擦力的变化不明显,但椭圆状微动循环图的短半轴开始变大,甚至开始向平行四边形转变(60 N载荷下),这意味着微动运行区域逐步由部分滑移区转换到滑移区. 在50 μm位移下,载荷为30、60和90 N时,微动磨损均处于滑移区,清除磨屑后摩擦力均出现了下降的现象,这些条件下微动循环图的变化与在30 μm位移和30 N载荷下微动循环图的变化相同.
在清除磨屑之后,继续进行微动磨损试验2万周次. 通过对比第99 500、83 500以及74 500周次下的微动循环图可知,在清除磨屑之后,又进行一定周次的微动磨损,微动循环图能恢复到清除磨屑之前的形状.这个结果说明在清除磨屑之后进行的这些周次的微动磨损,能产生大量磨屑. 在这个过程中,两接触体中间磨屑的产生和排出逐渐达到平衡. 随着磨屑的不断积累,微动磨损恢复到了清除磨屑之前的状态.
2.2 清除磨屑对摩擦系数的影响
图6所示为在清除磨屑之后,不同试验条件下摩擦系数随周次的变化曲线. 结果表明,在不同的施加位移下,微动磨损处于部分滑移区时,清除磨屑之后摩擦系数的变化不明显;然而,当微动磨损处于滑移区时,清除磨屑之后,摩擦系数会出现1个逐步上升的阶段,然后达到稳定,回到清除磨屑之前的水平. 由此可知,在微动磨损过程中清除磨屑对处于滑移区的微动磨损的摩擦系数影响较大,对处于部分滑移区的微动磨损的摩擦系数影响较小.
2.3 清除磨屑对系统形变量的影响
将1.2节中列出的相关周次下的系统形变量计算出来,然后用平滑的曲线连接,得到不同施加位移和不同载荷下系统形变量随周次的变化曲线(图7). 由图7可知,在试验清除磨屑之前,即微动周次小于80 000周次时,各个试验条件下的微动磨损都已经达到了稳定阶段. 然而,清除磨屑之后,大多数试验条件下系统形变量都会有所下降,只有一些处于部分滑移区的试验条件下,在清除磨屑后系统形变量几乎不变或者变化较小. 这是因为,当微动磨损处于稳定阶段后,如果在滑移区和混合区,由于上下试样间存在较大的相对滑动,有大量的磨屑产生,清除磨屑对系统形变量影响较大;而在部分滑移区时由于相对滑移较小,产生的磨屑也较少或者几乎不产生磨屑,清除磨屑带来的影响也较小.
另外,当微动磨损处于较大载荷的滑移区时,系统形变量在清除磨屑后的变化要比微动磨损处于较小载荷的滑移区更大. 这是因为,在大载荷下的滑移区,磨损更加严重,导致接触面之间的磨屑更多,在载荷较大的试验中清除磨屑,相比于载荷较小的试验,会有更多的磨屑被清除,由于原本储存的磨屑较多,因此清除磨屑后对系统形变量的影响也相应较大.
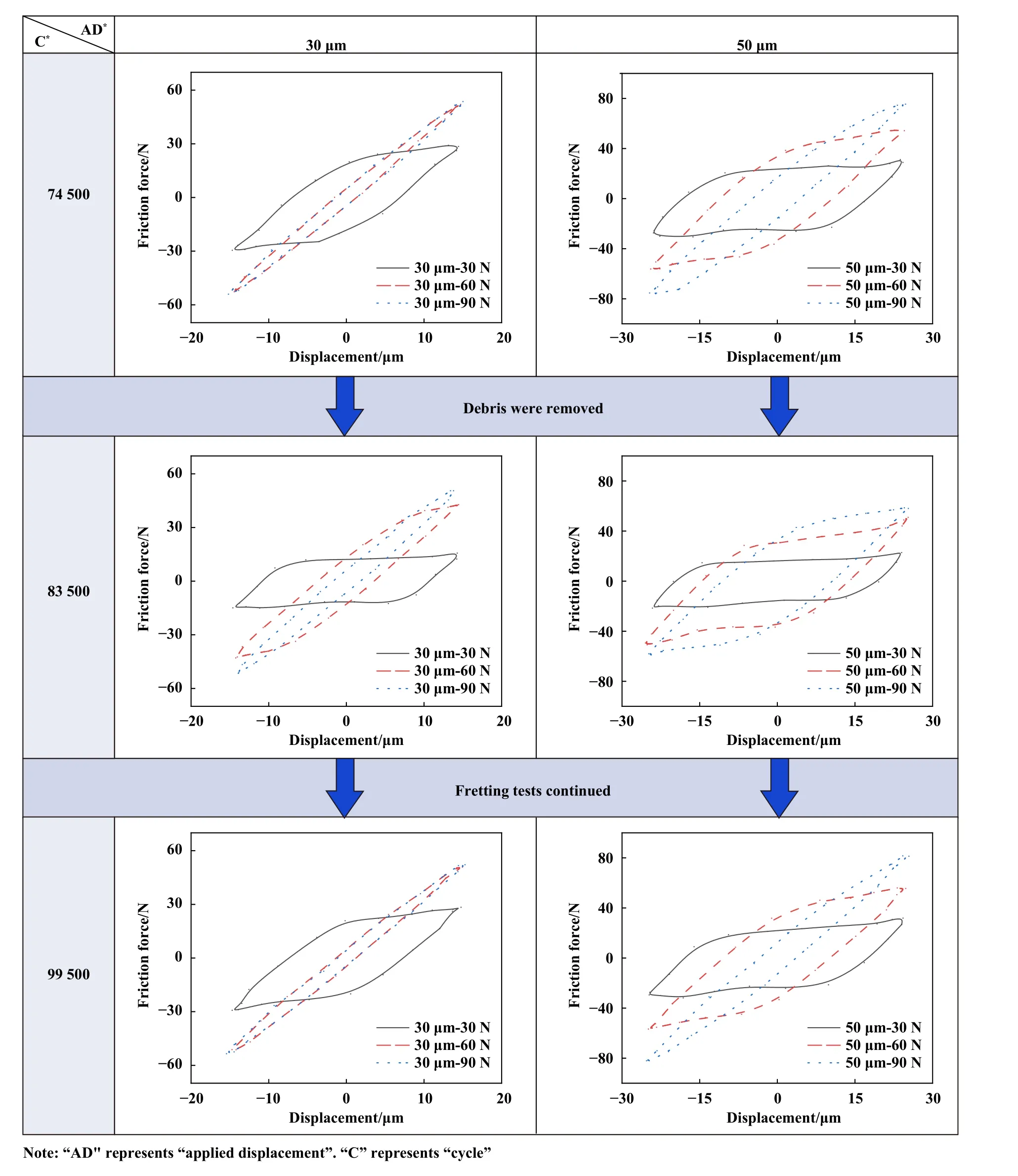
Fig. 5 Fretting loops of different cycles and different loads under the applied displacement of 30 μm and 50 μm图5 在30和 50 μm施加位移下,不同微动周次和不同载荷下的微动循环图
图8对比了不同施加位移下,在清除磨屑后系统形变量随载荷的变化. 结果显示,在第84 500、89 500、94 500和99 500微动运行周次下,随着载荷的增加,系统形变量都是最先在20 μm施加位移下达到1个稳定值,随着载荷继续增加,在30、40和50 μm施加位移下,也依次达到稳定的值. 并且,在清除磨屑之后运行的周次越多(例如第99 500周次和第84 500对比),上述规律越清晰明了,波动越小. 这与随着微动磨损过程的进行,磨屑的产生和排出逐渐达到平衡,磨损逐渐趋于稳定有关.
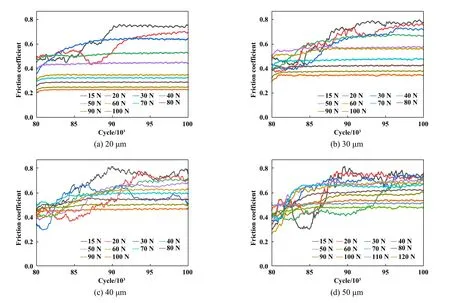
Fig. 6 Friction coefficient curves with fretting cycle after removing the debris under different applied displacement and different load图6 在不同的施加位移和载荷下,清除磨屑之后的摩擦系数随微动周次的变化曲线
由图8可以得知,当微动磨损处于滑移区时,在不同的施加位移下,系统形变量差别不大,且和载荷存在着线性关系. 因此,在不同的微动周次下,对特定载荷下滑移区的系统形变量取平均值,然后进行线性拟合,得到图9. 从线性拟合的结果可以看到,4条直线的斜率大致相等而截距有所差别. 直观地反映在图像上的结果就是,4个不同运行周次下的直线相互平行,随着运行周次的增加,直线整体上移,也就是同一载荷下,系统形变量增大. 这是由磨屑累积导致的. 直到94 500周次之后,磨屑的产生和排出达到平衡,直线便保持相对稳定.
2.4 磨屑的分布及尺寸
为了更清楚地探究磨屑在接触面之间的分布状态,在试验结束后,用导电胶分别在平面试样和球试样上粘取磨屑,以此来保证磨屑的分布状态不被改变,然后在扫描电镜下观察磨屑形貌,结果如图10所示. 结果表明从平面试样和球试样上粘取的磨屑均可分为两类:留在磨损区域的磨屑和被排出到磨损区域之外的磨屑. 通过平面试样上磨屑的放大照片[图10(c)]可以看出,留在磨损区域的磨屑呈块状,而被排出到磨损区域之外的磨屑呈细小的颗粒状. 块状的磨屑将两个接触面间隔开,能够在接触面相互运动时起到一定的缓冲作用. 根据前期的研究可以得知[29],外部的小颗粒磨屑是由中部块状的磨屑随着磨损的进行被不断地碾碎并排出到磨损区域之外形成的. 另外,对比图10(a)和图10(b)还可得知,平面试样上没有磨屑的区域(A、B和C区域),正好和球试样上磨屑聚集的区域(A*、B*和C*区域)互补,这个现象说明小颗粒磨屑是相对均匀地从各个方向被排出到接触区域之外的.
对外部小颗粒状的磨屑进行放大观察,结果如图11所示,可见大多数磨屑颗粒的尺寸较小,少部分磨屑颗粒较大,并且这些较大的颗粒是由一些较小的颗粒聚集在一块组成的. 根据kirk等[15]的研究可知,在微动磨损中,较小的颗粒状的磨屑会烧结成大块的颗粒,这是由于金属的氧化以及摩擦能量的耗散会导致接触表面的局部温度迅速升高[30],加之法向载荷和剪切载荷的影响,部分小颗粒会被压实. 而在高温的作用下,这些被压实的颗粒便被烧结成了尺寸较大的颗粒状磨屑[15]. 在图11中,对大颗粒磨屑的A点和小颗粒磨屑的B点进行能谱分析(表2),结果显示,大颗粒磨屑A中氧的质量分数明显高于小颗粒磨屑B中氧的质量分数. 这个结果同样能够佐证部分小颗粒磨屑团聚和烧结,进而形成较大颗粒的磨屑.
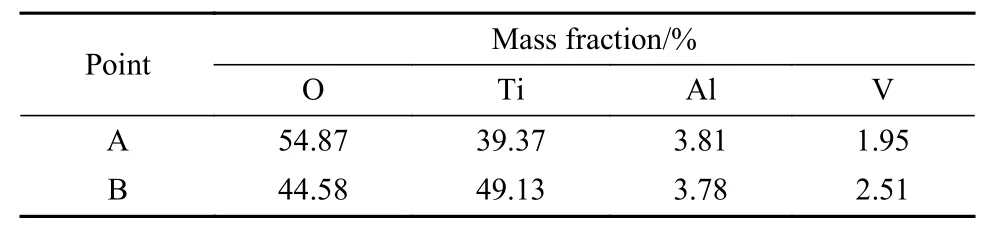
表2 磨屑的EDS结果Table 2 EDS results of debris
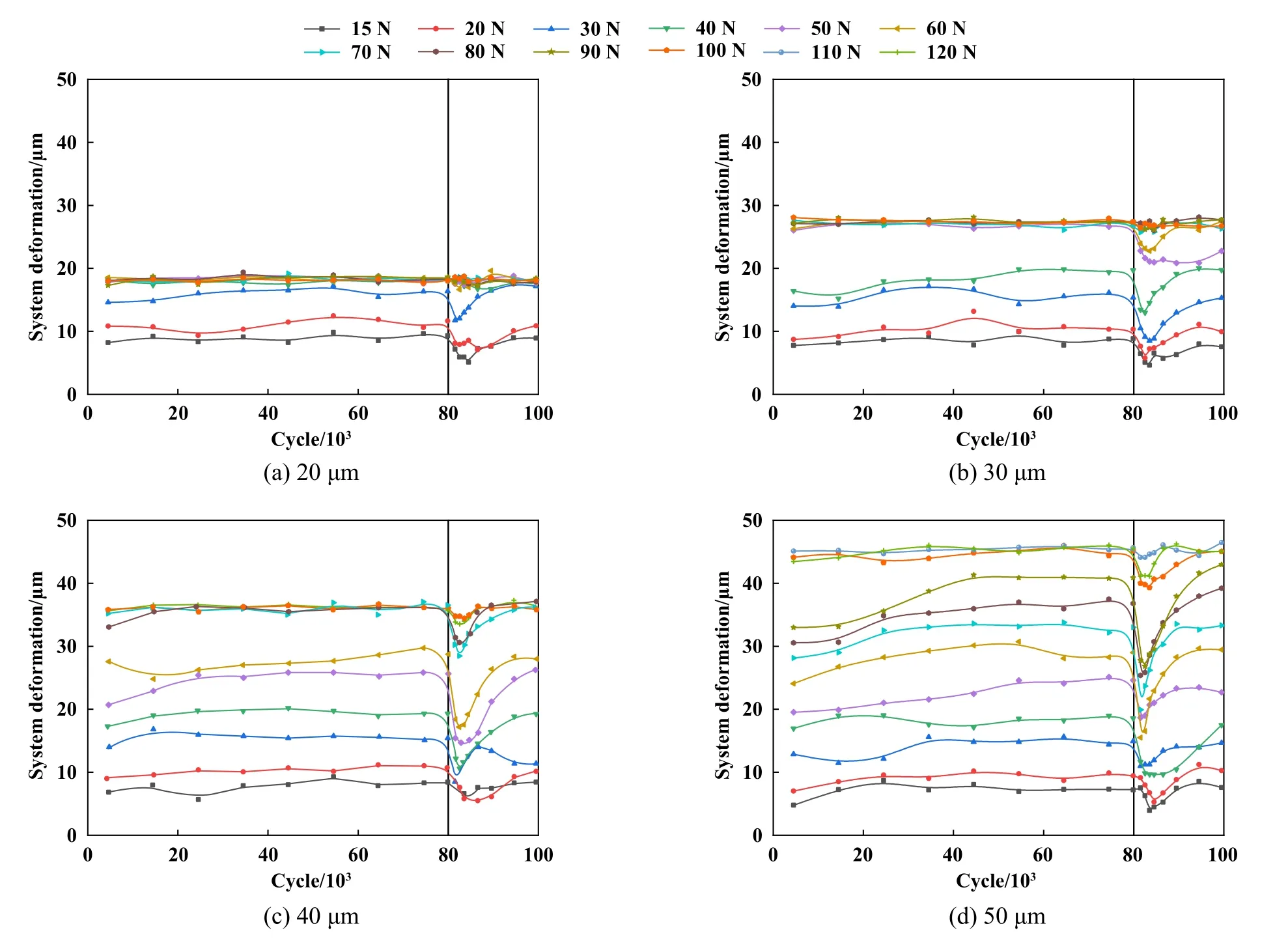
Fig. 7 Variation curves of system deformation with fretting cycles under different test parameters图7 在20、30、40和50 μm的施加位移以及不同载荷下,系统形变量随微动周次的变化曲线
对磨屑的尺寸进行统计,如图12所示. 结果表明,磨屑的尺寸集中在0.2~1.5 μm,并且尺寸在0.5 μm左右的磨屑最多. 据此可以推测,单个小颗粒磨屑的尺寸应该以0.5 μm为中心的正态分布. 而由于部分小颗粒磨屑被烧结成大颗粒,因此磨屑尺寸的分布曲线在大于0.5 μm的一侧偏离了正态分布.
2.5 制备表面织构储存磨屑对微动磨损的影响
通过清除磨屑的试验可以研究接触面之间没有磨屑或者仅存在较少磨屑对微动磨损的影响,而在样品表面制备沟槽状的表面织构可以储存磨屑,进而能探究接触面之间存在较多的磨屑对微动磨损的影响.为了将微动运行区域控制在滑移区,设置施加位移为40 μm,载荷为20、40和60 N,其他参数和之前的试验参数相同. 图13所示为有无表面织构的样品在40 N载荷下微动磨损试验结束后磨屑的分布情况. 结果显示,当样品的表面没有织构时,磨屑会较为容易地从接触区域溢出;而当样品有垂直于微动方向的沟槽状表面织构时,大量的磨屑会被束缚在接触区域[31],因此,在这个样品上的磨屑更多、磨屑层更厚.
将无织构样品第83 500周次(清除磨屑后继续微动磨损试验的第3 500周次)的系统形变量、无织构样品清除磨屑前达到稳定阶段的摩擦系数和系统形变量、有表面织构的样品达到稳定阶段的摩擦系数和系统形变量与载荷的关系绘成折线图(图14),用以反映接触区域中磨屑量对摩擦系数和系统形变量的影响.图14(a)中,在20、40和 60 N的载荷下,清除磨屑之后的摩擦系数分别从清除磨屑之前的1.06、1.04和0.99下降到0.39、0.46和0.44,在20 N载荷下降幅最大,达到63%. 在有表面织构的样品上,织构储存磨屑,导致摩擦系数增大, 20、40和 60 N的载荷下,摩擦系数分别为1.28、1.11和1.12,相较于无表面织构清除磨屑之前的样品,增幅同样在20 N载荷下最大,达到了21%.根据Halliday等[32]以及Fayeulle等[33]的研究,细小的磨屑在接触面之间能够降低摩擦系数,而被烧结、团聚在一起的大颗粒磨屑则会增大摩擦系数. 由图11可知,团聚的大颗粒磨屑数目较多且分布较广,并且结合图10可知,分布在磨损区域中部的是较大的块状磨屑. 因此,在大颗粒磨屑存在的情况下,掩盖了小颗粒磨屑降低摩擦系数的作用. 而在清除磨屑的过程中,大颗粒的磨屑会更容易被清除出去,进而导致摩擦系数降低;在存在表面织构的情况下,大颗粒磨屑堆积更多,进而导致摩擦系数较无织构的样品更大.
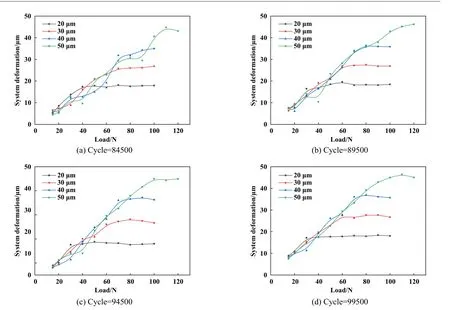
Fig. 8 Variation curves of the system deformation with the load under the fretting cycle number of 84 500, 89 500, 94 500 and 99 500图8 在第84 500、89 500、94 500和99 500微动运行周次时,对比不同施加位移下系统形变量随载荷的变化曲线
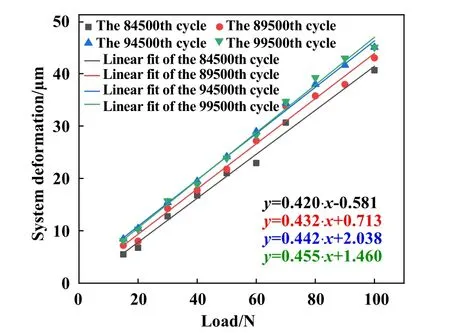
Fig. 9 Linear relationships between system deformation and load in the gross slip regime under different cycles图9 清除磨屑后不同运行周次下滑移区的系统形变量与载荷的线性关系
类似于摩擦系数,磨屑越多,系统形变量也越大.图14(b)中,在20、40和60 N的载荷下,清除磨屑之后的系统形变量分别从清除磨屑之前的10.78、19.15和28.73 μm下降到6.36、11.60和17.92 μm,在20 N载荷下降幅最大,达到41%. 另外,在有表面织构的样品上,表面织构储存磨屑,导致系统形变量增大,在20、40和60 N的载荷下系统形变量分别为12.42、21.08和33.62 μm,相比于没有表面织构的样品在清除磨屑之前的情况,系统形变量在60 N载荷下的增幅最大,达到了17%.这是因为,磨屑作为第三体材料,又较为疏松,能在两个接触面之间起到缓冲的作用,接触面之间的磨屑越少,缓冲越小,在外力作用下的变形能力也就越差[34].而系统形变量反映的是在微动磨损中通过系统自身的变形来减小相对滑动的能力. 清除磨屑之后,接触面之间的缓冲小,变形能力差,也就代表此时的系统形变量比稳定阶段的系统形变量更小;当存在垂直于微动运动方向的沟槽状表面织构时,磨屑被大量储存,接触面之间的缓冲好,变形能力强,此时系统形变量较无织构时更大.
3 结论

Fig. 10 SEM micrographs of debris collected from the plate and the ball samples after fretting wear under the load of 40 N and the applied displacement of 40 μm图10 在40 N载荷、40 μm施加位移下的磨损试验结束之后,从平面和球试样上收集到的磨屑的SEM照片

Fig. 11 SEM micrograph of debris图11 磨屑形貌的SEM照片
a. 清除磨屑之后继续微动磨损试验,摩擦力和摩擦系数会下降,进而导致微动循环图会由“高瘦”变成“矮胖”;随着微动磨损的进行,磨屑的产生和排出重新达到平衡之后,微动循环图又会恢复到清除磨屑之前的形状.
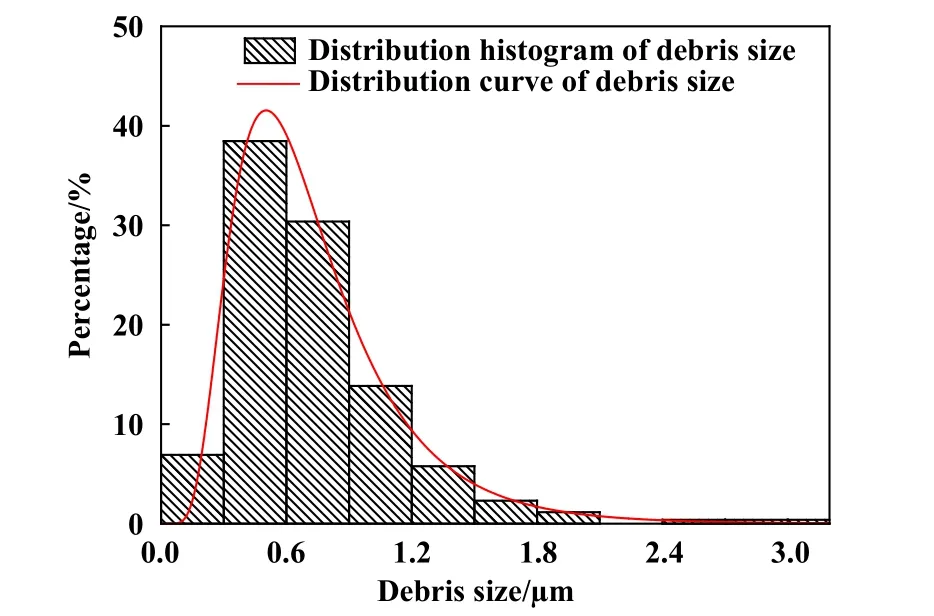
Fig. 12 Distribution histogram and distribution curve of the debris size图12 磨屑粒径的分布直方图以及分布曲线
b. 磨损区域中部的磨屑呈块状,而被排出到磨损区域之外的磨屑呈松散的颗粒状,其尺寸集中在0.2~1.5 μm,并且尺寸在0.5 μm左右的磨屑最多. 在载荷以及高温的作用下,一些小颗粒的磨屑会被烧结成较大的颗粒,导致磨屑尺寸的分布曲线在大于0.5 μm的一侧偏离了正态分布.
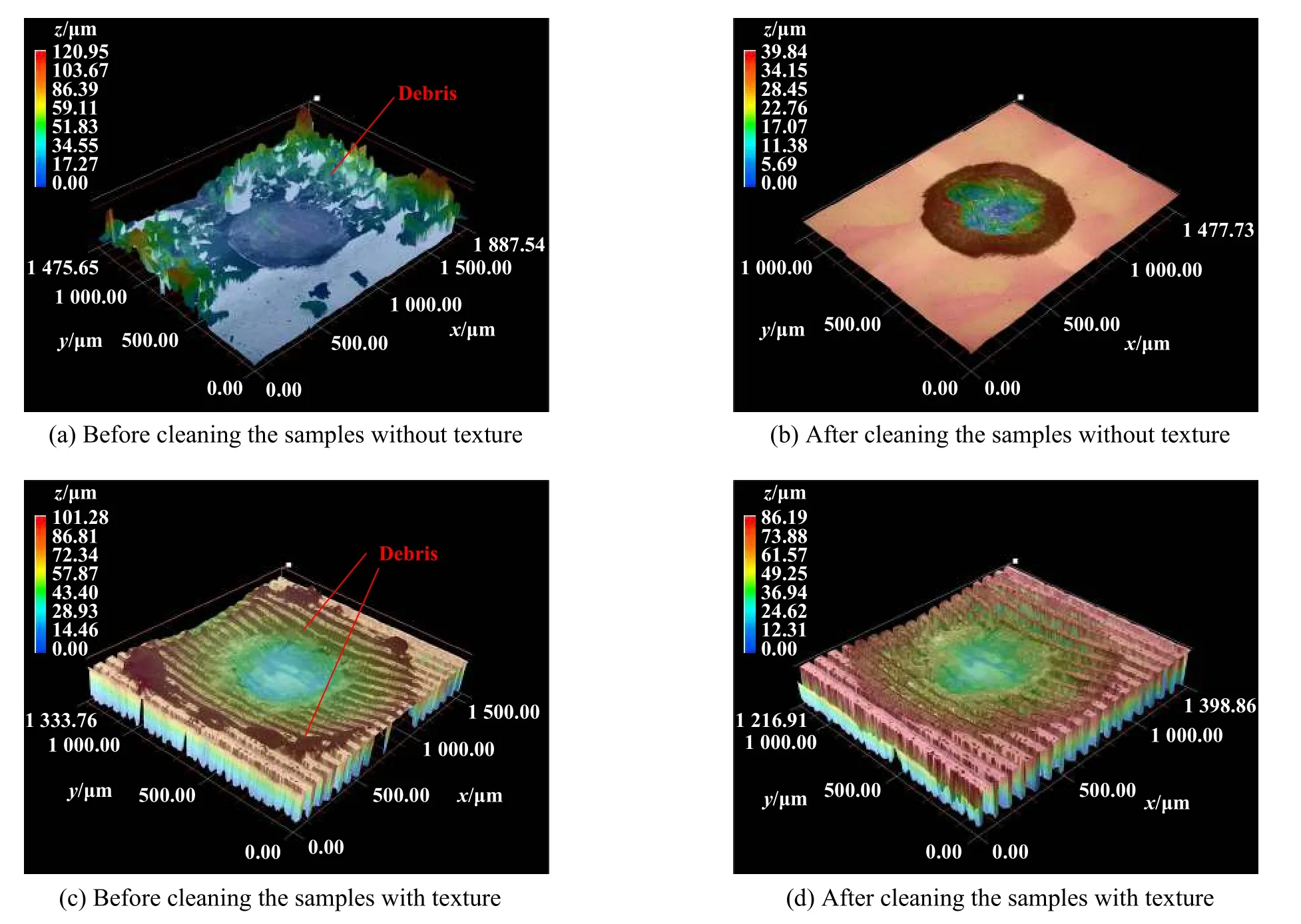
Fig. 13 The distribution of debris of different samples under the load of 40 N and the applied displacement of 40 μm图13 在40 N载荷、40 μm施加位移下,不同样品的磨屑分布
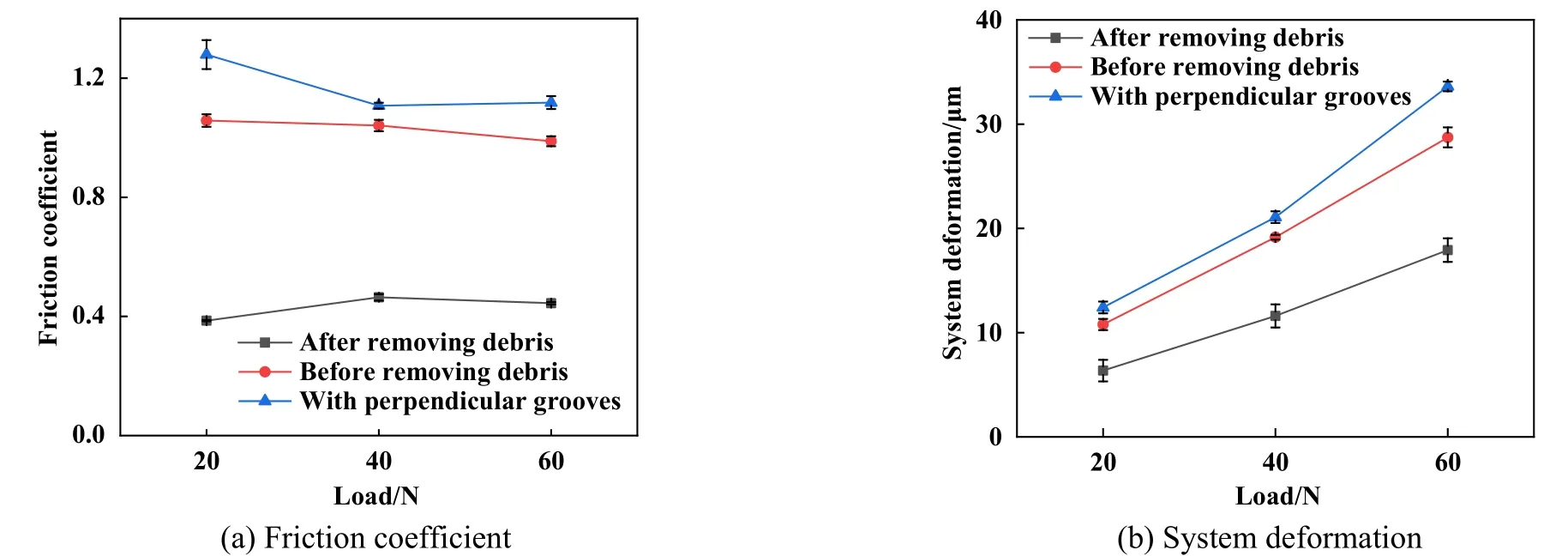
Fig. 14 Comparison of (a) friction coefficient and (b) system deformation under the applied displacement of 40 μm when fretting run in gross slip regime under three conditions图14 在40 μm施加位移下微动磨损处于滑移区时,三种条件下(a)摩擦系数和(b)系统形变量的对比
c. 当样品有垂直于微动方向的沟槽状表面织构时,接触面之间磨屑较多,摩擦系数和系统形变量比无织构时的更大,其中在20 N载荷下的增幅最大,分别为21%和47%. 当清除磨屑后,接触面之间的磨屑较少,摩擦系数和系统形变量比清除磨屑之前更小,其中在20 N载荷下的降幅最大,分别为63%和41%.
d. 在大颗粒磨屑存在的情况下,掩盖了小颗粒磨屑降低摩擦系数的作用. 而在清除磨屑的过程中,大颗粒的磨屑会更容易被清除出去,进而导致摩擦系数降低;在存在表面织构的情况下,大颗粒磨屑堆积更多,导致摩擦系数较无织构的样品更大.
