区间毕达哥拉斯犹豫模糊集的不确定性研究
2021-01-08李龙妹郑婷婷尹文静
李龙妹,郑婷婷,尹文静
(安徽大学 数学科学学院,安徽 合肥 230601)
0 引言
现实世界中存在着大量的不确定、不完整的信息,Zadeh[1]提出的模糊集理论是解决这类问题的有效工具。许多学者在此基础上进行了深入的研究,并推广至直觉模糊集[2](Intuitionistic fuzzy set, IFS),区间直觉模糊集[3],毕达哥拉斯模糊集[4](Pythagorean fuzzy set,PFS)等。但当多位专家对某项决策出现犹豫不决、决策难以达成一致时,上述的模糊集方法显得有些力不从心。为解决此类问题,Torra[5]提出了犹豫模糊集的概念,其元素的隶属度是由一般模糊数组成的集合,从而包含所有专家在决策中产生的模糊信息。人们在犹豫模糊集的基础上进一步研究,产生了对偶犹豫模糊集[6]、直觉犹豫模糊集[7]、区间直觉犹豫模糊集[8]等概念,这些理论已经成功应用到聚类分析、模式识别、多属性决策等领域。现实世界可能会存在隶属度和非隶属度之和大于1的情形,此时在直觉模糊环境下就不能解决此问题。Yager[4]提出了毕达哥拉斯模糊集,其中隶属度和非隶属度的平方和小于等于1,显然毕达哥拉斯模糊集的应用范围比直觉模糊集更广泛。近年来一些学者把犹豫模糊集和毕达哥拉斯模糊集结合在一起,提出了毕达哥拉斯犹豫模糊集,但不同的学者对此的定义不同,Khan[9]和Liang[10]认为任意一个元素的隶属度与非隶属度是两个独立的犹豫模糊数。Wei[11]认为一个毕达哥拉斯犹豫模糊数是几个毕达哥拉斯模糊数组成的集合。Zhang[12]研究了区间毕达哥拉斯犹豫模糊集 (Interval-valued Pythagorean hesitant fuzzy set,IVPHFS),将每个区间毕达哥拉斯犹豫模糊数 (Interval-valued Pythagorean hesitant fuzzy element,IVPHFE) 视为几个区间毕达哥拉斯模糊数 (Interval-valued Pythagorean fuzzy element,IVPFE) 的集合,该理论更适合描述复杂模糊的环境。她提出了IVPHFS的一些算子,并把它们应用到群决策问题中。Zheng[13]构造了一系列IVPHFS相关系数,并用它们去解决聚类和多属性决策问题。到目前为止,关于区间毕达哥拉斯犹豫模糊环境下的不确定性问题的研究还很少。
模糊集的不确定性一直是模糊集理论的研究热点之一。这其中最重要的度量指标就是熵和相似度。熵是度量不确定信息的重要组成部分。熵值越大,说明信息越模糊。相似度反映的是两个模糊集之间的近似程度。相似度越大,说明两个模糊集越接近。它们在模式识别、属性决策、医疗诊断等领域都有非常广泛的应用。1968年Zadeh[14]首先提出了模糊熵的概念,用于度量模糊集的模糊程度。Burillo和Bustiuse[15]进一步给出了直觉模糊熵的公理化定义。Mao[16]结合直觉度、模糊度和区间跨度提出了新的区间直觉模糊熵和混合熵的概念,并基于混合熵作为相似性度量成功应用于多属性决策问题。Xu[17]给出了犹豫模糊熵、犹豫模糊集相似性度量的公理化定义。Peng[18]研究了毕达哥拉斯模糊集的各种信息测度间的关系,包括距离测度、相似度、熵等。Peng[19]还继续推广研究了区间毕达哥拉斯模糊集(Interval-valued Pythagorean fuzzy set,IVPFS)的相似度。然而目前对IVPHFS的模糊熵和相似度的研究还少见报道。为探究区间毕达哥拉斯犹豫模糊集的不确定性,本文提出了区间毕达哥拉斯犹豫模糊熵的公理化准则,定义了区间毕达哥拉斯犹豫模糊熵,并将其应用到属性权重完全未知的区间毕达哥拉斯犹豫模糊多属性决策中,为解决多属性决策问题提供一种新的思路。
本文首先介绍了区间毕达哥拉斯模糊集和区间毕达哥拉斯犹豫模糊集的定义和相关知识,然后定义区间毕达哥拉斯犹豫模糊集的模糊因子和直觉因子,并给出区间毕达哥拉斯犹豫模糊熵的公理化准则。基于香农熵和两个因子去构造区间毕达哥拉斯模熵,证明其符合公理化准则。之后基于模糊贴近度提出区间毕达哥拉斯犹豫模糊集的相似性度量,在此基础上给出了加权相似度公式。最后利用新提出的熵和相似度去解决毕达哥拉斯犹豫模糊环境下的多属性决策问题。
定义1[2]设X是一个有限论域,称A为论域X上的一个区间毕达哥拉斯模糊集IVPFS,定义为:
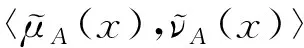
定义2[12]设X是一个有限论域,称A为论域X上的一个区间毕达哥拉斯犹豫模糊集IVPHFS其定义为:
A={〈x,hA(x)〉|x∈X},
其中
当IVPHFEs中IVPFEs的个数全为1时,一个IVPHFS退化为一个IVPFS。当所有IVPFEs都满足μ-=μ+,ν-=ν+时,一个IVPFS退化成一个PFS。当所有毕达哥拉斯模糊数满足μ+ν≤1时,一个PFS退化成一个IFS。
1 区间毕达哥拉斯犹豫模糊熵
熵可以有效地度量模糊信息,熵值越大,表明信息越模糊。考虑到区间毕达哥拉斯犹豫模糊集的不确定性由模糊因子和直觉因子两部分构成,下面给出模糊因子和直觉因子的定义:
定义3设A∈IVPHFS(X),则A的模糊因子定义为:
ΔA(x)=
A的直觉因子定义为:
ψA(x)=

下面根据模糊因子和直觉因子来定义区间毕达哥拉斯犹豫模糊熵的公理化准则:
定义4设映射E:IVPHFS(X)→[0,1],对于A∈IVPHFS(X),若E(A)=F(ΔA,ψA),且E(A)满足以下准则:
(1)E(A)=0当且仅当A是X上的清晰集,即∀x∈X,hA(x)={〈x,[1,1],[0,0]〉}或hA(x)={〈x,[0,0],[1,1]〉};
(2)E(A)=1当且仅当∀x∈X,hA(x)={〈x,[0,0],[0,0]〉};
(3)E(A)=E(AC);
(4)E(A)随ΔA(x)的增大而减小,随ψA(x)的增大而增大。
则称E(A)为区间毕达哥拉斯犹豫模糊熵。
下面根据香农熵来定义区间毕达哥拉斯犹豫模糊熵。
设G(x)=-[xlog2x+(1-x)log2(1-x)]是香农熵,其中x∈[0,1]。
定义5设A∈IVPHFS(X),定义:
定理1定义5中的E(A)是一个区间毕达哥拉斯犹豫模糊熵。
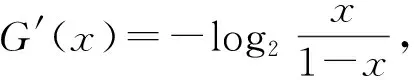

(1)E(A)=0
⟺∀x∈X,hA(x)={〈x,[1,1],[0,0]〉}或
hA(x)={〈x,[0,0],[1,1]〉}。
(2)E(A)=1
⟺∀x∈X,hA(x)={〈x,[0,0],[0,0]〉}。
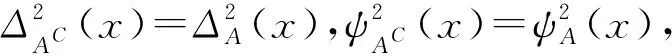
(4)设x=ΔA(x),y=ψA(x),
其中x∈[0,1],x2∈[0,1],y∈[0,1],y2∈[0,1]。对x,y求偏导,结果如下:
因此F(x,y)随x的增大而减小,随y的增大而增大,所以F(ΔA,ψA)随ΔA(x)的增大而减小,随ψA(x)的增大而增大。即E(A)随ΔA(x)的增大而减小,随ψA(x)的增大而增大。
综上知定义5中的E(A)满足定义4中的公理化条件。
2 区间毕达哥拉斯犹豫模糊集的相似性度量
相似度可以衡量两个IVPHFSs之间的差异,相似度越大,说明两者越相近;相似度越小,则反映出两者的区别越大。
采用Peng[20]的方法对IVPFEs从大到小依次进行排序。

分别为A和B的得分函数,
分别为A和B的精确函数。
(1) 如果K(A)>K(B),则A≻B;
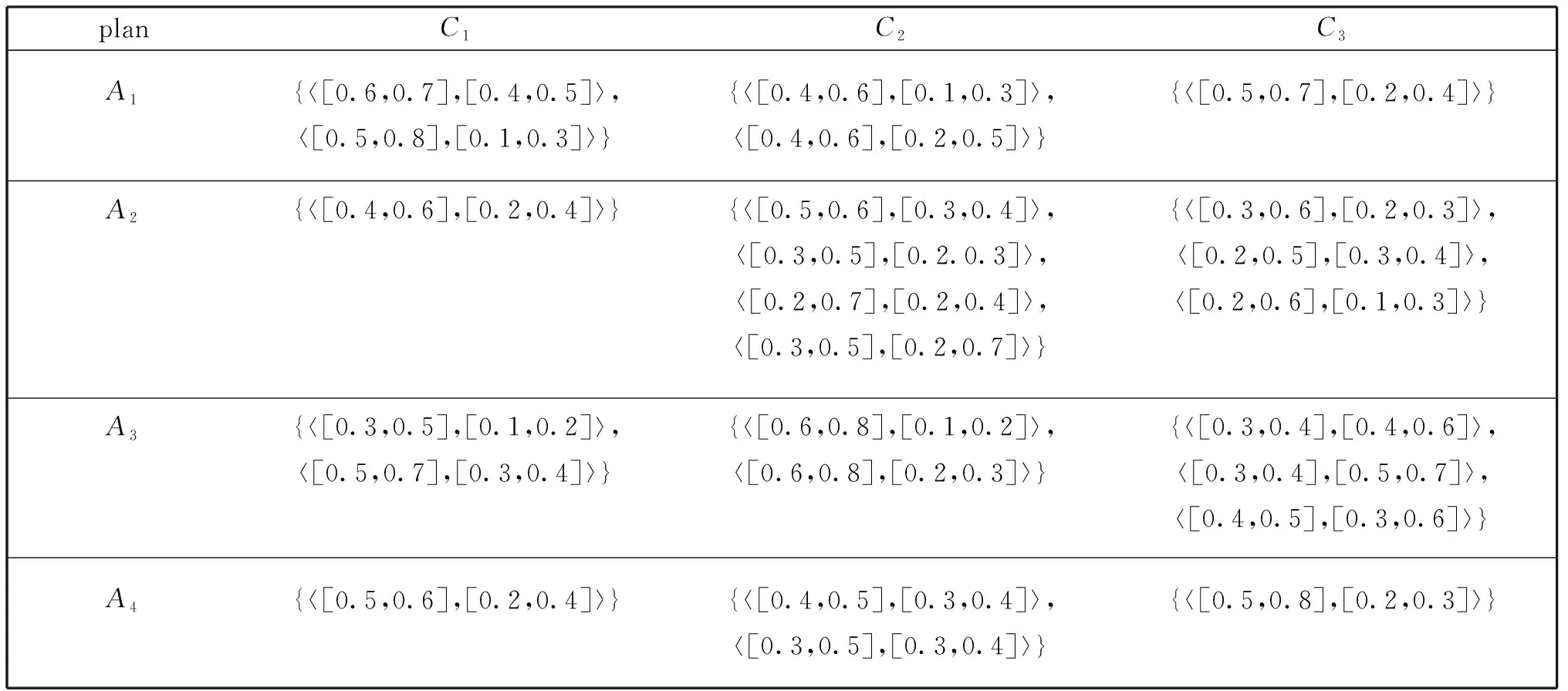
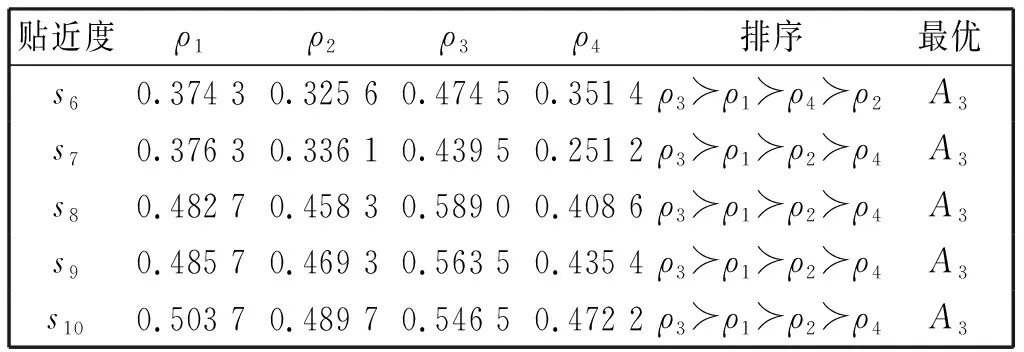
(2) 如果K(A) (3) 如果K(A)=K(B),则 当H(A)>H(B),则A≻B; 当H(A) 当H(A)=H(B),则A=B。 不同的IVPHFEs中IVPFEs的个数可能不同,为了解决这个问题,本文采用最小公倍数法[13]对IVPHFEs进行扩充。 对某个IVPHFE中的IVPFEs进行排序扩充后,基于模糊贴近度给出区间毕达哥拉斯犹豫模糊集的相似性度量。 定义8设A,B∈IVPHFS(X),则A与B之间的相似度定义如下: s1(A,B)= s2(A,B)= 其中 σ(j)表示IVPHFE中IVPFEs重新排序扩充后的第j大的IVPFE,LA(xi)为|hA(xi)|和|hB(xi)|的最小公倍数。 性质1设A,∈IVPHFS(X),定义8的5个相似度具有以下性质: (1)0≤s(A,B)≤1; (2)s(A,B)=s(B,A); (3)s(A,B)=1⟺A=B。 证明下面以s1为例: (2)显然s1(A,B)=s1(B,A)。 (3)如果s1(A,B)=1,则 即 可得A=B。 如果A=B,则 可得 故s1(A,B)=1。 s2,s3,s4,s5的证明过程与s1类似。 例1 设A,B∈IVPHFS(X),X={x},其中 A={x,〈[0.2,0.3],[0.4,0.5]〉, 〈[0.4,0.5],[0.2,0.3]〉}, B={x,〈[0.4,0.5],[0.2,0.3]〉, 〈[0.2,0.3],[0.4,0.5]〉}。 如果不对其中的IVPFEs进行排序,以s1为例:s1(A,B)=0.7544。但经过排序后得到 A′={x,〈[0.4,0.5],[0.2,0.3]〉, 〈[0.2,0.3],[0.4,0.5]〉}, B′={x,〈[0.4,0.5],[0.2,0.3]〉, 〈[0.2,0.3],[0.4,0.5]〉}。 且s1(A,B)=s1(A′,B′)=1。 从上述例子会发现,在探讨两个IVPHFSs间的相似性时,我们需要对每个IVPHE先进行排序,如果不进行排序则相似度可能会不满足性质1中的性质(3)。 当IVPHFS退化为IVPFS时,设A,B∈IVPFS(X),以s1为例: s1(A,B)= 其中 当两个IVPFSsA,B退化为PFSs时, 进一步,当A,B继续退化为IFSs时, 其中 以上退化后所得s1均满足性质1中的三条性质。 同样可以发现s2,s3,s4,s5经过上述退化后与s1的情形类似,均满足性质1中的三条性质。 定理2设A,B,C∈IVPHFS(X)。如果si(A,B)=1,si(A,C)=1,则si(B,C)=1 (i=1,…,5)。 证明由性质1中的(3)知si(A,B)=1 ⟹A=B,si(A,C)=1⟹A=C,所以B=C,因此si(B,C)=1 (i=1,…,5)成立。 上述讨论的IVPHFSs中每个元素所占比重相同,但实际问题中,元素所占比重往往是不同的。下面介绍IVPHFSs的加权相似性测度。 显然s6,s7,s8,s9,s10满足性质1中的3条性质。 在实际的决策问题中,不同属性所提供信息的重要性可能是不同的,此时可通过属性权重加以区分。熵可以有效地度量模糊信息,熵值越小,信息越清晰。当属性权重完全未知时,我们可以通过熵权法来计算属性权重。一个属性的熵值越小,则属性所占的权重越大,否则对于决策者来说,该属性所提供的信息越不重要。 算法步骤如下: (2)计算属性权重 (1) (3) 计算每个方案的贴近度 (2) (4)对贴近度进行排序,ρi越大,则选择Ai越优。 一个投资公司根据Cj(j=1,2,3)这三个指标来评估四个方案Ai(i=1,2,3,4),其中C1和C2为效益型,C3为消费型,专家给出决策矩阵[15]如表1。 (1) 正理想解: A+={{〈[0.5,0.8],[0.1,0.3]〉}, {〈[0.6,0.8],[0.1,0.2]〉}, {〈[0.3,0.4],[0.5,0.7]〉}}; 负理想解: A-={{〈[0.3,0.5],[0.1,0.2]〉}, {〈[0.3,0.5],[0.2,0.7]〉}, {〈[0.5,0.8],[0.2,0.3]〉}}。 (2) 通过公式(1)算得属性权重结果如下: ω1=0.326 2,ω2=0.322 0,ω3=0.351 8。 (3) 分别用s6,s7,s8,s9,s10来计算方案与正负理想解之间的相似度,再由公式(2)计算贴近度,表2为在5个相似度下方案的贴近度及其排序。 (4) 从表2可以看出ρ3总是最大的,即A3是最优方案。此结果与文献[13]中的结果一致。 表1 区间毕达哥拉斯犹豫模糊决策矩阵 表2 排序 区间毕达哥拉斯犹豫模糊集是区间毕达哥拉斯模糊集和犹豫模糊集的推广,其在多属性决策、聚类分析、模式识别等方面有广泛的应用。本文首先提出了区间毕达哥拉斯犹豫模糊熵的公理化准则,基于模糊因子和直觉因子定义了一个区间毕达哥拉斯犹豫模糊熵。然后基于模糊贴近度提出了区间毕达哥拉斯犹豫模糊集间的相似性度量。最后用提出的熵和相似度去解决区间毕达哥拉斯犹豫模糊环境下的多属性决策问题。实例结果证明了方法的合理性和有效性。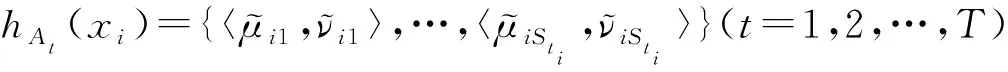
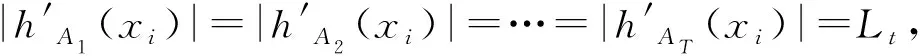

3 多属性决策
3.1 算法步骤

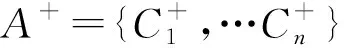
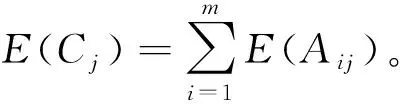
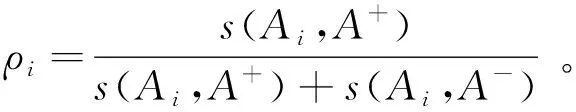
3.2 实例分析
4 结论
