E-广义凸直觉模糊集①
2014-07-09李选海范传强
李选海, 刘 锋, 范传强
(1.海军大连舰艇学院,基础部,辽宁大连116018;2.东北大学,系统科学研究所,辽宁沈阳110004;3.辽宁石油化工大学理学院,辽宁抚顺113001)
0 引言
凸集及其性质是最优化领域的一个重要研究课题.同样,凸模糊集也是模糊数学中研究的一个热点.本文通过将 E - 广义凸模糊集[1~4]、凹模糊集[5]和凸直觉模糊集[5~6]相结合,提出了 E - 广义凹模糊集和E-广义凸直觉模糊集,从而推广了E-广义凸模糊集,并对它们的性质进行了初步研究,得到了一些好的理论结果.本文把现有的凸模糊集理论研究向前推进一小步,从而能引出一个相对较新的研究方向和领域,先行为解决未来出现的新问题提供理论支撑.
1 预备知识
定义 1.1[1]设 A ∈F(X),设 λ,μ ∈[0,1],且λ < μ,∀l∈[0,1],若存在E:X→X,使得∀x,y∈ X,有 A(lE(x)+(1-l)E(y))∨ λ≥A(E(x))∧A(E(y))∧μ,则称A为 E -(λ,μ〛一凸模糊集,简称E-广义凸模糊集.
定义1.2[5]设为n维欧氏空间,X的模糊子集A被称为凹模糊集,如果∀λ∈[0,1],x,y∈X,有A(λx+(1-λ)y)≤A(x)∨A(y).
定义1.3[5]设X为欧氏空问,若μA为X的凸模糊集且υA为X的凹模糊集,则称直觉模糊集(X,μA,υA)为X的凸直觉模糊集.
定理1.1[1]设A,B ∈ F(X)是广义凸模糊集,则A∩B是广义凸模糊集.
2 E-广义凹模糊集和E-广义凸直觉模糊集
定义2.1 设A ∈F(X),设 λ1,λ2∈[0,1],且 λ1> λ2,∀l∈[0,1],若存在 E:X → X,使得∀x,y∈X,有 A(lE(x)+(1 -l)E(y))∧ λ1≤A(E(x))∨A(E(y))∨λ2,则称A为 E - (λ1,λ2〛一凹模糊集,简称E-广义凹模糊集.
定理2.1 设A,B∈F(X)是E-广义凹模糊集,则A∪B是E-广义凹模糊集.
证明: 设λ1,λ2∈[0,1],且λ1> λ2,∀l∈[0,1],∀x,y∈ X,则有
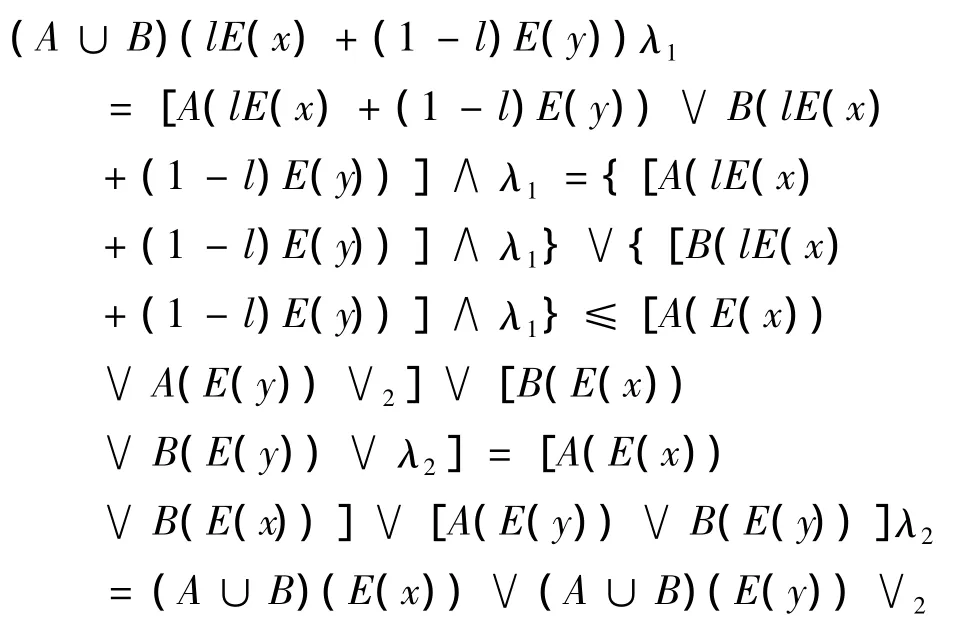
因此,A∪B是E-广义凹模糊集.
定理2.2 设Ai∈F(X),i∈I(I是指标集)是E-广义凹模糊集,则Ai是E-广义凹模糊集.
证明: 与定理2.1证明类似,故略.
定理2.3 设f为欧氏空间X到Y的可逆线性映射,若A∈F(X)是E-广义凹模糊集,则f(A)为Y上的E1-广义凹模糊集,其中E1:f(X)→f(E(X))为E:X→X的派生函数.
证明: 设λ1,λ2∈[0,1],且λ1> λ2,∀l∈[0,1],∀y1,y2∈ Y,则有 ∃!x1,x2∈ X,s.t.f(x1)=y1,f(x2)=y2,
所以,

因此,f(A)为Y上的E1-广义凹模糊集.
定义 2.2 设 A ∈ IFS(X),设 λ1,λ2∈[0,1],且λ1< λ2,∀l∈[0,1],若存在E:X→X,使得∀x,y∈ X,有 μA(lE(x)+(1 - l)E(y))∨ λ1≥μA(E(x))∧ μA(E(y))∧ λ2,υA(lE(x)+(1 -l)E(y))∧(1-λ1)≤υA(E(x))∧υA(E(y))∨(1 - λ2),则称A为 E - (λ1,λ2]一广义凸直觉模糊集,简称E-广义凸直觉模糊集.
定理2.4 设A,B∈IFS(X)是E-广义凸直觉模糊集,则A∩B是E-广义凸直觉模糊集.
证明: 设λ1,λ2∈[0,1],且λ1< λ2,∀l∈[0,1],∀x,y∈ X,则有


因此,AB是E-广义凸直觉模糊集.
定理2.5 设Ai∈IFS(X),i∈I(I是指标集)是E-广义凸直觉模糊集,则Ai是E-广义凸直觉模糊集.
证明: 与定理2.4证明类似,故略.
定理2.6 设f为欧氏空间X到Y的可逆线性映射,若A∈F(X)是E-广义凸直觉模糊集,则f(A)为Y上的E1-广义凸直觉模糊集,其中E1:f(X)→f(E(X))为E:X→X的派生函数.
证明: 设λ1,λ2∈[0,1],且λ1< λ2,∀l∈[0,1],∀y1,y2∈ Y,则有 ∃!x1,x2∈ X,s.t.f(x1)=y1,f(x2)=y2,所以有
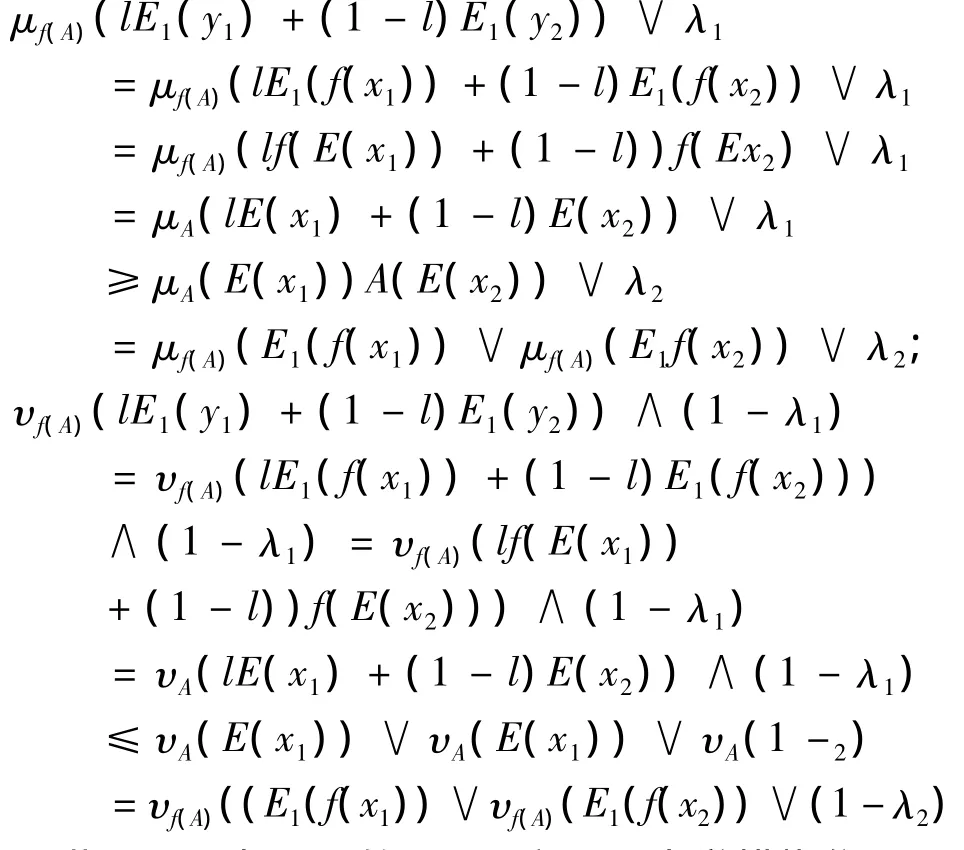
因此,f(A)为Y上的E1-广义凸直觉模糊集.
故命题得证.
[1] 刘卫锋.E-广义凸模糊集和E-广义反凸模糊集[J].云南师范大学学报,2012,32(6):39-44.
[2] 鞠红梅,袁学海,陈图云.凸模糊子集的再定义[J].模糊系统与数学,2001,15(1):68-70.
[3] 顾惠,廖祖华.广义Fuzzy凸集[J].模糊系统与数学,2004,(18):153-156.
[4] 廖祖华,黄昱,居世宾.反凸模糊集[J].江南大学学报:自然科学版,2005,4(4):431 -433.
[5] 沈正维,徐国俊.凹模糊集和凸直觉模糊集[J].辽宁师范大学学报:自然科学版,1997,20(4):278 -280.
[6] Atanassov K.Intuitionistic Fuzzy Sets[J].Fuzzy Set and Systems ,1986,20:|87 - 96.
