基于GRU-Attention的无监督多变量时间序列异常检测

郑育靖,何强*,张长伦,2,王恒友

(1.北京建筑大学 理学院,北京 100044;2.北京建筑大学 北京未来城市设计高精尖创新中心,北京 100044)

0 引言

时间序列数据异常检测一直是学术界和工业界的热点问题。对异常点的检测以及对异常区域的定位可以在关键时刻提供重要信息,人们才能有针对性地干预异常事件,达到防止或消除异常的效果。时间序列数据异常检测在工业、金融、军事、医疗、保险、关键系统安全、机器人、多智能体、网络安全、物联网等领域[1-2]都受到人们的关注。

所谓时间序列的异常检测,就是在时间序列数据中检测出少部分具有离群、震荡等异常情况的点。通常情况下异常占整体时间序列的比例很低,人们希望通过算法,学习到原始数据的分布或其他特征来实现对异常点的成功捕捉。单变量异常检测是对仅存在一个特征的时间序列上展开的,由于只有一个维度的数据,可以应用很多传统滤波算法,例如Spectral Residual算法[3]。多变量时间序列异常检测指对具有多个特征的时序数据进行异常检测,这类问题是在单变量时序异常检测的基础上扩展而来。多变量时序数据异常的出现往往是由多个特征共同决定,对每个特征单独分析无法准确判断异常。所以更合理的方法是对多个特征序列综合分析,进而识别出多个变量共同作用下的异常。

目前,多元时序异常检测在深度学习领域的研究取得了显著的进展。例如,Malhotra 等人[4]提出基于LSTM的编码器解码器网络,该网络对“正常”时间序列的重构概率进行建模,利用重构误差在多个传感器中检测异常。Hundman等人[5]利用长短时记忆网络(LSTM)来检测基于预测误差的航天器多元时间序列。Ding等人[6]提出了一个基于分层时间记忆(Hierarchical Temporal Memory, HTM)和贝叶斯网络(Bayesian Network, BN)的实时异常检测算法RADM,提高了实时异常检测的性能。然而,已提出的模型往往依赖循环神经网络学习数据的性质或分布,没有考虑特征间的关系和数据固有的周期性等性质,故本文提出了基于GRU-Attention的无监督算法,从时间维度和特征维度两个角度充分利用数据信息进行异常检测。

本文的主要贡献如下:

(1)提出了一种新的无监督多变量时间序列异常检测框架,模型在三个公共数据集上展示了优越性能。

(2)模型在预测部分利用GRU-skip弥补传统预测模块在长期记忆上的缺陷。

(3)模型通过案例的图像分析部分,验证贡献大的特征对识别异常的重要性。

(4)本文模型对于异常点具有较好的可解释性。

本文在第1节给时间序列异常检测相关工作。在第2节介绍基于GRU-Attention的无监督检测方法。在第3节从实验上验证本文所提方法的有效性。最后总结全文。

1 时间序列异常检测

异常检测在其他相关领域也被称为新颖性检测、离群值检测或事件检测[7]。时间序列异常检测是其中一个深受人们关注的问题。根据在训练过程中是否使用标签可以分为监督,半监督以及无监督异常检测。监督学习方法[8]需要标记数据进行模型训练,只能识别已知的异常类型[9],因此应用范围有限。时序异常检测研究方法主要关注无监督问题。根据数据中特征的个数可以将问题分为单变量时序异常检测和多变量时序异常检测。单变量时序异常检测[3,10-11]只考虑特征是否符合长期特性,当数据值与总体分布有较大差异时将其视为异常实例[12-17]。多变量问题在每个时间戳上有多个特征[18]。现有的多元时间序列异常检测方法主要可以分为两类:一、基于单变量的异常检测[19]:通过单变量算法对每个特征进行单独监控,最后将结果汇总给出最终判断。二、直接进行异常检测[5,20-23]:将多个特征同时考虑,从而进行算法分析。Zong等人[24]提出的利用深度自编码器来生成低维的数据,表示每个输入数据点的重构误差,输入到高斯混合模型中(GMM)来进行多变量异常检测。LSTM-VAE算法[7]是基于编码解码器的LSTM网络,对时间序列进行误差重构,运用重构误差对若干传感器进行异常检测。LSTM-NDT[5]是一种无参数阈值选取的无监督算法,该文目标是在没有利用随机信息的情况下,建立一个异常检测系统来监测航天器发回的由相关领域专家标记好的数据。Gugulothu等人[25]通过端到端学习框架,将非时间维度约简技术和周期性自动编码器结合起来,用于时间序列建模。OmniAnomaly[26]提出了一种随机递归神经网络,通过随机变量建模数据分布,从而捕获多变量时序的正常模式。

本文针对无监督的多维时间序列异常检测,对多条线数据直接进行预测,并考虑异常点的可解释性。模型的可解释性部分与OmniAnomaly模型相比,不仅考虑了预测与实值的均方根误差,还考虑了特征的信息,对于数据信息的利用更全面可靠。

1 基于GRU-Attention的无监督检测方法

1.1 问题阐述

1.2 网络结构

本文模型分为两部分:预测部分与误差阈值选取部分。如图1所示,多变量时间序列数据同时输入到基于时间预测层和基于特征预测层中,所得结果拼接后进行线性变换即为预测结果。预测结果与真实值的均方根误差输入到误差阈值选取部分,超过设定的误差上限则认为该时刻出现异常。

图1 网络结构Fig.1 Overall structure

模型从两个方面对多变量时序进行预测:

1) 基于时间预测层:为了更好地捕捉时间序列长期特征,本文运用Gated Recurrent Unit (GRU)进行时序预测。考虑到数据可能存在周期性以及GRU无法记忆长期历史数据,运用GRU-skip来弥补这些缺陷,捕获时序数据之间的更深层关系。相关内容将在1.3节解释。

2) 基于特征预测层:在特征维度上运用注意力机制,得到每个变量对预测时刻的贡献,从而帮助进行时序预测。相关内容将于1.4节讲述。

1.3 基于时间预测层

GRU细胞内的结构经过精心设计,以更好地记忆历史信息,缓解RNN的梯度消失问题,从而捕获信息之间的长期关系。然而,GRU在实际应用中往往不能捕捉到长时间变量的相关性,仍旧存在梯度消失的问题。根据文献[27],可以在GRU中增加一个跳跃组件来缓解这个问题,本文将这一结构称为GRU-skip。此组件针对具有周期性这一特性的数据,具体来说就是在当前隐藏单元与相邻周期内同一相位的隐藏单元增加跳转链接,更新过程如公式(1)。

rt=σ(Wr·[ht-p,xt])

zt=σ(Wz·[ht-p,xt])

yts=σ(Wo·ht) 。

(1)

GRU-skip的输入是CNN的输出。其中p是一个超参数,表示当前隐藏单元与其向前跨越p个单元建立了链接。这个跳跃链接的建立对于周期不太明显或是具有动态周期的数据集而言效果欠佳。

(2)

图2 基于时间预测层Fig.2 Time-based prediction layer

1.4 基于特征预测层

对于多维时间序列而言,不同变量的重要性不同,即对于待测点的权重不同。特征维度的信息对于异常检测十分关键,以往模型并没有重视此维度的信息。文献[28]将注意力机制运用到时间序列预测中得到了良好的效果。因此为了充分利用特征维度上每个变量的重要性这一信息,本文在特征维度上应用了注意力机制。

目前,注意力模型被广泛应用于深度学习的各个领域,如图像处理、自然语言处理、语音识别等。它的核心操作是从序列中学习每个元素的重要性,得到每个元素对应的权值参数,然后根据重要性合并元素,权重参数是由这个注意力系统分配给元素的系数。

如图3所示，将原始数据Xt={xt-w,xt-w+1,…,xt-1,xt}∈Rw×m输入到维持特征维度不变的GRU层中，得到输出Gt={gt-w,gt-w+1,…,gt-1,gt}∈Rw×m，gt是t时刻GRU的输出。之后，用k2个1×w的卷积核(w是滑动窗口大小)对Gt的行向量进行卷积操作，得到每个变量在时间维度上的深层特征，卷积结果用不同颜色正方形表示。所有卷积核扫过隐藏状态的m个特征得到矩阵HC∈m×k2,此处激活函数仍选择ReLu。卷积输出指的是第j个卷积核扫过gt-w+1,gt-w+2,…,gt-1的第i个变量的结果，接下来通过得分函数计算每个变量的得分α，即每个变量对预测时刻的重要性。传统的注意力机制的得分函数如下：

(3)

(4)

(5)

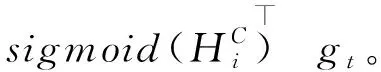
(6)

为减少参数提高效率，本文选择(3)作为得分函数。得分函数：1×k2×Rk2×11,αi∈R1。αi越大意味着变量i对预测时刻t的贡献越大，影响也越大。最后选择sigmoid函数是因为在大多数情况下，softmax函数用于分类问题，输出是互斥的。sigmoid函数的输出并不互斥，意味着可以同时选择多个变量。在这里，我们希望得到每个变量的重要性，而不仅仅是重要性最大的变量，故激活函数选择sigmoid。

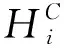
(7)

(8)

(9)

1.5 误差阈值选取

预测模型的损失函数选择均方根误差(RMSE)：

(10)

将测试集输入到训练好的预测模型中，得到的测试集中每个观测点的预测值与真实值的均方根误差记为{l1,l2,…,lQ}∈Q，并运用极值理论(EVT)中的POT(Peaks over Threshold)模型对这个子序列选取阈值。

极值理论是寻找序列中极值规律的一种统计理论，一般认为极值在异常检测问题中就是要寻找的异常点,它们在大多数情况下位于分布的尾部。极值理论的优势在于无需对数据分布进行假设并且可以通过参数选取达到自动设置阈值的目的。其第二定理POT表明：大于某阈值的样本服从广义帕累托分布(GPD)。因此，通过POT去选取阈值th：

(11)

(12)

q是L>th的比例，Q是观测值个数，Qth是L>th的个数。用POT做阈值选取，需要调参过程。

图3 基于特征预测层Fig.3 Feature-based prediction layer

2 实验与分析

2.1 数据集描述与数据预处理

为验证该模型的有效性，在以下三个数据集上进行实验:MSL (Mars Science Laboratory rover)、SMAP (Soil Moisture Active Passive satellite)和SMD (Server Machine Dataset)。其中，MSL和SMAP是美国NASA的两个航天器公共数据集[29]。SMD数据集[26]来自一家大型互联网公司长达五周的服务器数据，数据已发布在GitHub上。SMD分为数据大小相同的两部分，第一部分是训练集，第二部分是测试集。测试集上的异常数据已经由相关领域的专家进行了标记，其中，训练集和测试集分别包含28组数据，需要分开训练和测试，即训练集中第1组数据训练的模型，由测试集中第1组数据进行测试。最终SMD数据集中指标得分取的是28组数据的平均值。

MSL和SMAP数据集保持时间顺序被分成训练集(60%)、验证集(20%)和测试集(20%)，SMD数据集是已经分好的28组训练集与测试集中，分别训练之后一一对应分别测试。

表1 数据集信息

表1给出了三个数据集的详细信息，包括变量个数、训练集大小、测试集大小以及测试集中异常样本比例。对于多维时间序列而言不同变量的量纲不同，为了不让这种数值大小差异影响模型预测和阈值选择，运用最大最小归一化方法对所有数据进行预处理：

(13)

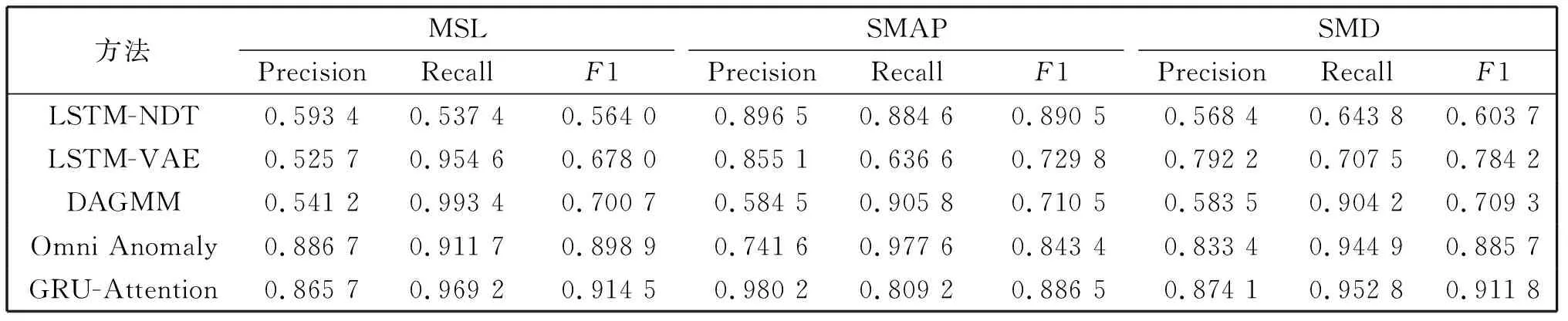
表2 模型性能比较

2.2 评价指标与参数设置

与大多异常检测问题相同，本文使用精度、召回率和F1-score来评估GRU-Attention和其他算法。计算方法如下：

Precision(P)=TP/(TP+FP)，

(14)

Recall(R)=TP/(TP+FN)，

(15)

(16)

其中，TP和FP分别表示真正例数和假正例数,FN指假负例数。上述三个指标的值越高，表明模型鲁棒性越强。

模型参数设置：滑动窗口w都取100,使用Adam优化器训练100次，学习率是0.1，GRU-skip中的p=20,两个预测层中卷积核个数k1=k2=200，基于时间预测层中d=6,GRU隐藏层维度为300，阈值选取中q=0.001。

2.3 模型比较

本部分将展示与其他4种模型在三个数据集上的比较结果，比较的模型包括有LSTM-NDT[5]、LSTM-VAE[7]、DAGMM[24]、OmniAnomaly[26]。如表2所示，GRU-Attention具有良好的泛化能力,在两个数据集上取得最高的F1值，在SMAP略低于最优结果。

LSTM-NDT在SMAP上有很高得分，但是在MSL和SMD数据集上表现较差，体现出该模型对不同场景十分敏感。而本文模型在不同数据集上表现稳定且性能优异。

短期信息对于多元时序也很重要，DAGMM的性能不够理想的原因是没考虑短期信息。模型GRU-Attention使用GRU以及GRU-skip来捕捉时序的短期和长期的依赖性，这些设计有助于获得比DAGMM更好的鲁棒性。本文还进行附加消融实验(见2.4节)以比较不同部分设计的有效性。OmniAnomaly应用了随机模型，将变量看成随机变量进而学习其分布，在三个数据集上都有很高的性能体现。该模型局限性在于没有利用特征维度上变量间的关系，GRU-Attention在特征维度应用注意力机制有效提高了模型性能，在三个数据集上得分都高于OmniAnomaly。

2.4 模块有效性

为了更好说明预测部分每个组件设计的必要性和有效性，本文增加了四组对比试验。分别在原始模型中的预测部分去掉基于时间预测部分、基于特征预测部分、基于时间预测部分的GRU和GRU-skip模块再进行训练，最后进行测试。并且对于去掉不同组件之后的模型，都将参数个数调整到与原始模型参数个数相近，从而避免模型复杂度对于各个模块有效性分析的影响。

去掉时间预测层中的传统预测部分GRU：模型记为w/o GRU。预测层的输出直接为特征预测层与GRU-skip结果拼接后进行线性变换得到。

去掉时间预测层中的GRU-skip部分：模型记为w/o GRU-skip。预测层的输出直接为特征预测层与GRU-skip结果拼接后进行线性变换得到。

从表3来看，不同模块对于不同数据集的影响不同。对于MSL数据集而言，去掉特征预测层后F1值降低15%，GRU-skip对其影响次之。时间预测层对SMAP影响最大，其他部分的影响比较平均。在SMD上的数据显示所有的组件对于异常检测都很关键，F1值降低超过18%，尤其是GRU部分的缺失使得模型性能降低了近27%。通过这一部分的实验，说明本文模型每个模块的设计是必要且有效的。

2.5 异常点解释性评估

多变量异常检测比单变量异常检测复杂的原因在于异常的出现可能是多个特征共同作用的结果，因此能否找到导致异常出现的特征至关重要。异常点解释性评估指评估模型找到导致异常出现的关键特征的能力。SMD数据集的28个测试集标出了导致异常出现的特征，其他数据集均没有相关信息，故本文仅在SMD数据集上做异常点解释性的评估计算。将特征对观测点xt的重要性定义为ASt：

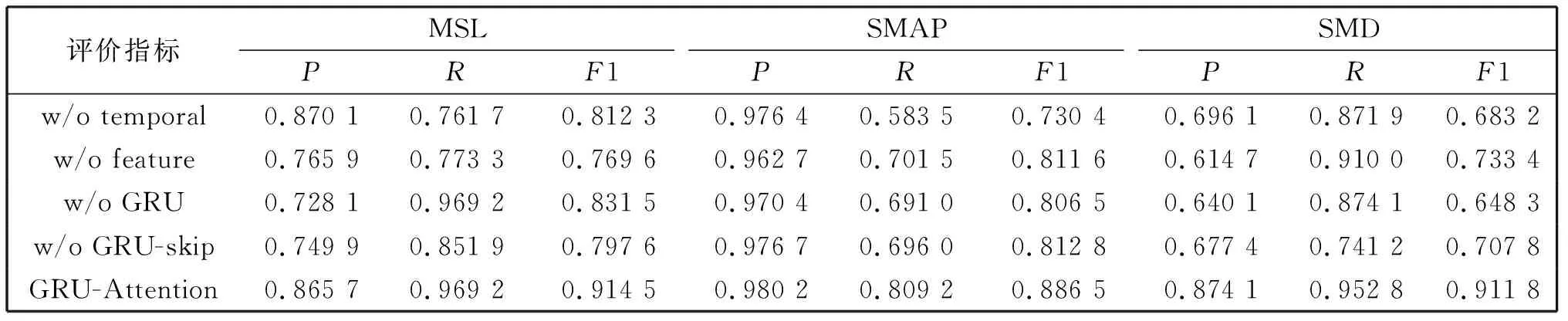
表3 模块有效性比较

图4 案例分析Fig.4 Case study

ASt=losst+at，

(17)

losst=(yt-xt)2∈Rm，

(18)

其中，yt是预测模型对t时刻的预测值，xt是真实值，losst为预测值与真实值的均方根误差，yt,i与xt,i(i=1,2,…,m)之间误差越大意味着第i个特征出现异常的可能性越大，对xt的影响也越大。αt∈1×m是特征预测层中注意力机制得到的每个特征对预测点的贡献，αt越大显然对xt影响越大。因此，本文将这两部分相加定义为特征对于待测点的重要性。

之后，将ASt中的值按重要性大小排序，将其对应的特征记录在ASLt中，故ASLt中就是按照重要性大小排序的特征。将SMD数据集中提供的对xt起主要影响的特征记为GTt，由于尚无评估异常点解释性的标准度量，故本文采用文献[17]相同的评估方法：

(19)

此处，|GTt|是真实情况下造成t时刻出现异常的特征个数。Hit@P×|GTt|是指ASLt中的前P×|GTt|个特征与GTt中的特征重叠的个数，P取1和1.5。假设xt是异常点，模型得到的导致异常出现的特征降序为ASLt={3，6，15，21，10，18}，GTt={6，15}，则P=1时，HitRate@P=0.5；P=1.5时，HitRate@P=1。在SMD中的28个数据集分别进行上述过程后取平均值之后得到HitRate@1=0.740 8；HitRate@1.5=0.794 3。可见，多数导致异常出现的特征都能被准确找到。

2.6 案例研究

前文提到注意力机制旨在将多条线对当前预测结果的贡献度进行量化，为了验证注意力机制获得得分的实际价值，在本节通过图4展示正常和异常点部分特征的原始图像进行分析。图4(a)展示数据正常时的情况：抽取该时间点的8个特征，按照注意力机制得到的得分α降序画出8个特征的原始数据曲线图,绿线是正常点的对应时刻。这个正常点得分高的特征有特征23、6、14、24。具有较高贡献度的特征23和特征6具有显著的周期性，并且周期性没有出现明显的震荡或者波动，贡献度较低的特征同样处于稳定状态。说明正常情况下，注意力机制侧重于关注周期性明显的特征，这些特征对于预测更为重要，故给予较高权重。对于长期是定值或是正常情况下取值范围波动较小的特征给予较少关注。

图4(b)展示数据异常时的情况，红线是异常点出现的时刻。可以看到贡献度最高的特征23的周期性被打破，明显出现异常。第二和第三条曲线代表的特征14和9都出现了明显的尖峰，显著的区别于之前正常情况下的平稳状态。第四条曲线可以看到异常时刻特征24的取值发生下降，显然不在正常时刻的取值范围内。得分较低的后四个特征取值没有出现异常。

通过以上的案例分析，得知注意力机制能够有效得到每个特征对于待测点xt的权重(即每个特征的重要性)。因此，注意力机制中得到的每个特征的得分可以作为衡量特征对预测点重要性ASt值(2.5节提到)的一部分。

3 结论

本文提出了一种新的多变量时间序列异常检测框架。通过利用多元时间序列的时间关系和特征关系联合进行预测。模型在三个公共数据集上优于其他的4种模型。除此之外，该模型拥有良好的异常点解释性，能够有效帮助人们寻找异常事件的实际根源，定位到出现异常的特征。未来的工作可能来自于两方面，第一，尝试将预测模型与重构模型结合，有望进一步提升模型的精度；第二,目前的异常诊断是在相对简单的场景下进行的，之后可以将模型来应用于复杂案例。