斜吹气流入射角对纱线折入的影响

刘宜胜，徐光逸

(浙江理工大学 机械与自动控制学院，浙江 杭州 310018)

近几十年，以片梭织机、喷气织机、剑杆织机为主要形式的织机占领了纺织工业的主要装备市场[1]。无梭织机的出现不仅大大提高了织造效率，而且能有效减少织机运转过程中的噪声，对优化工作环境、保护工人身体健康具有积极意义。有梭织机凭借其在梭子内的纡子可以织造出性能良好的光边织物；但是无梭织机具有机外供纬的特性，每根纬纱由于单向引纬的特点必须剪断，故存在布边问题[2]。

由于无梭织机中织物多为毛边下机，为了方便后续印染工序，引入折入装置以实现织物光边下机。折入装置分为气动和机械2种主要形式，机械折入装置应用更为广泛[3]。因气动折入装置自动化程度较高，近年发展也较快，其不仅可以有效避免机械折入装置由于机械部分加工误差所导致的装置不稳定性，而且可以在高速状态下持续工作。

近年来国内外对无梭织机的折入装置进行了一系列研究。刘培德等[4]开发了一种筘座直连式气动光边装置。其将气缸、纬纱剪刀机构、气动折边器整体安装到气缸定位座中形成一个整体，再通过气缸定位座连接到打纬筘座的槽上，实现整体随着打纬筘座一同摆动，提高了打纬操作的方便性，减少了零部件的磨损，延长了装置的使用寿命。郭岭岭等[5]在使用基于ZAX9100型喷气织机(日本津田驹工业株式会社)的无针折入装置对高密光边织物进行开发时，对钢筘的位置进行了设计微调，并且对各个时间斜吹和折入气流的压强进行设计，提高了生产效率。赵敬[6]针对其加工帘子布用的OMNIplus 800TC型喷气织机(比利时必佳乐公司生产)上使用的针头式折入装置进行了改进，使得装置可以随着钢架移动且不需要调整钢筘宽度。

Kim等[7]通过Spalart-Allmaras湍流模型和纳维-斯托克斯方程(Navier-Stokes equations)对喷气织机中纬纱通道的气流场进行分析，得到气流速度和纬纱表面受力存在较大联系的结论。纱线与气流场的仿真研究属于流固耦合范畴，其因学科交叉覆盖了广泛的研究领域[8]。以本文研究对象为例，在气流场和纱线的耦合系统中，一般的数值研究基于二者的耦合界面，流场通过力的作用在纱线表面影响纱线的运动，与此同时纱线的变形和运动使得周边的计算气流场区域和边界条件发生了改变。其研究方法可以归结为古典分析法、交错分析法和整体分析法，后二者的耦合方式均为双向流固耦合(fluid-structure interaction，FSI)[9]。

与固体颗粒不同，纱线具有长径比较大的特点，同时兼具弹性和柔性，故对其进行建模具有一定的难度。在不同的流体环境中有研究者通过直线段链、珠-簧链、黏弹性铰接多球链、有限单元等方式对其进行了复杂建模。 Osman等[10]通过建立以直线段链组成的柔性纬纱三维模型和二维超声速模型进行了单向和双向的流固耦合仿真模拟，并且仿真结果与实验有较高的相似度。对于装置结构设计和入射气流压强等设计参数已进行了较为深入的探究，但是缺少入射气流角度对于纱线运动轨迹影响方面的相关研究。

本文采用有限元分析软件(ADINA)搭建二维纱线和气流的双向流固耦合气流场模型，对不同入射角度的斜吹气流对纱线的运动轨迹的影响情况进行研究。并通过可编程控制器控制电气阀设定调节气动折入装置在不同入射角度下斜吹气流的气流压强和作用时间，以期对气动折入装置结构优化和其余参数设定提供理论参考。

1 气动折入装置仿真模型

采用ADINA软件对气动折入装置进行建模。气动折入装置二维气流场模型见图1。可以看出，模型具体结构与各个边界条件设定的情况。气流由斜吹孔和折入孔吹入并先后协同作用在纱线上，将纱线一端固定、一端自由以模拟纬纱未打入梭口时的状态。其仿真步骤如下：斜吹气流首先从压力入口进入，通过斜吹气流喷嘴射出后作用于纱线上端；在斜吹气流作用一定程度后，纱线在气流的作用下弯折至一定状态；关闭斜吹气流的同时打开折入气流，纱线在折入气流的作用下完成折入。

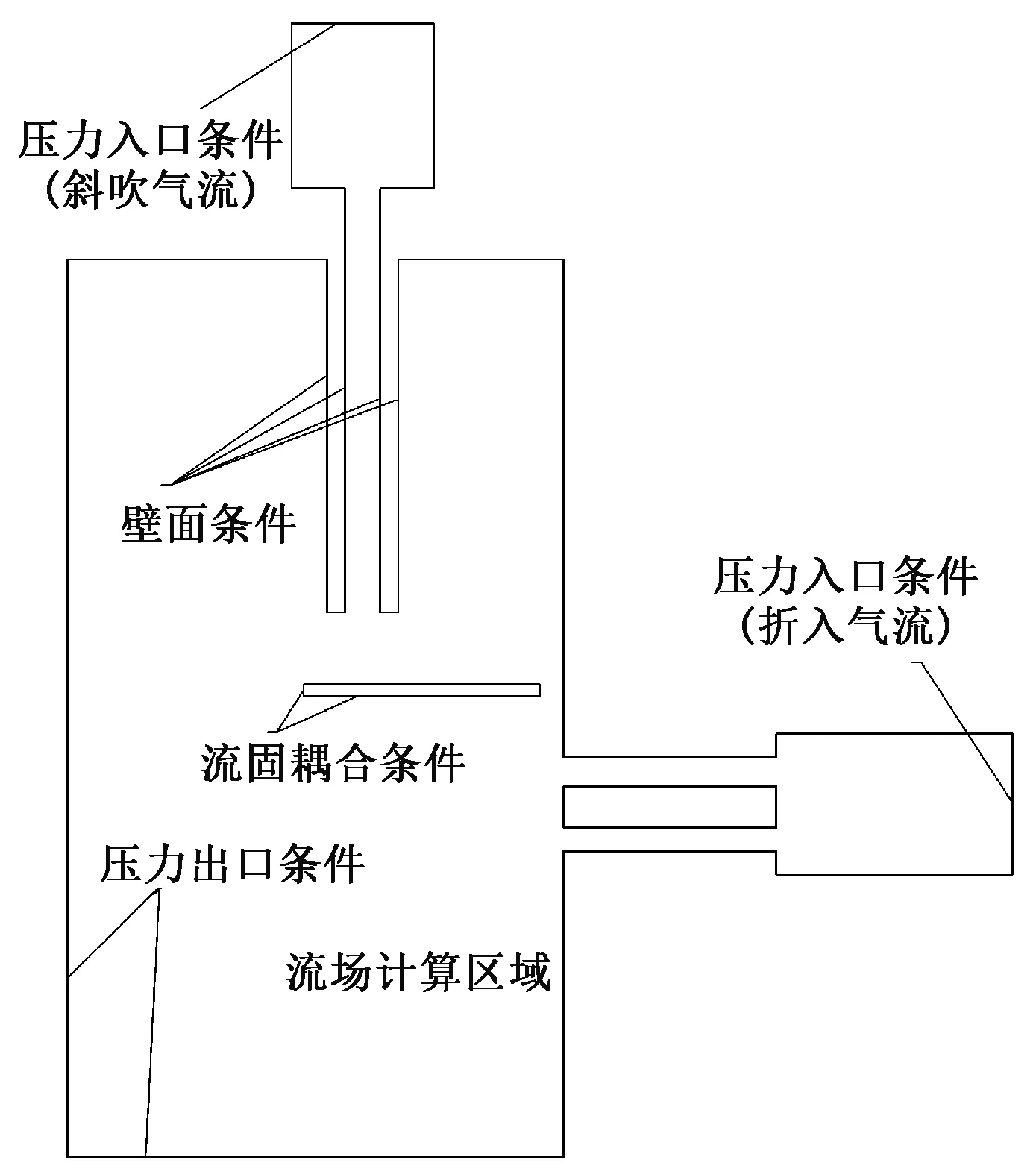
图1 气动折入装置二维气流场模型Fig.1 Two-dimensional airflow field model of pneumatic tucking device

1.1 数值模拟办法

在ADINA自带的双向耦合计算方法中，有直接计算法和迭代计算法2种不同的方法。直接计算法也可称为同时计算法，在此系统中流体和固体的变量完全耦合。其相较于迭代耦合法需要更多的内存，但因纱线和气流场数据在1个系统中进行计算，提高了仿真的准确率。本文选用直接耦合法对纱线和气流进行双向流固耦合的仿真分析。采用普通K-ε湍流模型建立气流场模型。在对湍流模型进行设置时采用系统缺省值，初始条件设定为标准大气压。在纱线模型建立时忽略重力对纱线的影响。实验采用的纱线线密度为55 tex，其直径为0.38 mm。根据公式计算得出纱线的密度为485 kg/m3，在实际建立仿真模型时将密度设置为500 kg/m3，弹性模量为8×10-7Pa，泊松比为0.307。仿真研究中的纱线忽略其粗糙表面，将其简化为各向同性的线弹性体。

1.2 边界条件与网格划分

将斜吹气流入口和折入气流入口设置为压力入口条件(图1)。在模型边界条件设定中，将气流孔孔壁设定为壁面条件，其余外部均设定为开放边界即压力出口条件。将纱线视为矩形，纱线边界设定为流固耦合边界。被边界条件所包围的区域即为计算流场区域。纱线模型和气流场模型需分开建模并对其进行网格划分。本文采用自适应的动网格技术应对计算过程中边界和网格的移动。

1.3 实验平台搭建和测试准备

本文基于自行设计的气动折入装置进行实验平台的搭建，气动折入装置实验平台见图2，可以看出实验时相关组件的工作流程。首先空压机产生的气流通过橡胶软管引导至ITV3030-014CS3-Q电气比例阀(日本SMC株式会社)，通过SIN-C702信号发生器(中国温州标诺仪器有限公司)控制电气比例阀对气流进行调压输出，并通过CP1H-XA40DT-D可编程控制器(欧姆龙自动化(中国)有限公司)设置的程序控制电磁阀1、2的开闭来实现喷嘴的异步动作。其中电磁阀1控制斜吹气流，电磁阀2控制折入气流。本文使用24 V稳压电源保证设备正常运行，并采用PCO.1200hs(德国PCO公司)高速摄像机对实验结果进行拍摄。通过对电气比例阀中的电流调节，分别实现斜吹、折入气流0.3、0.35、0.4 MPa这3种不同的实验入射压强。

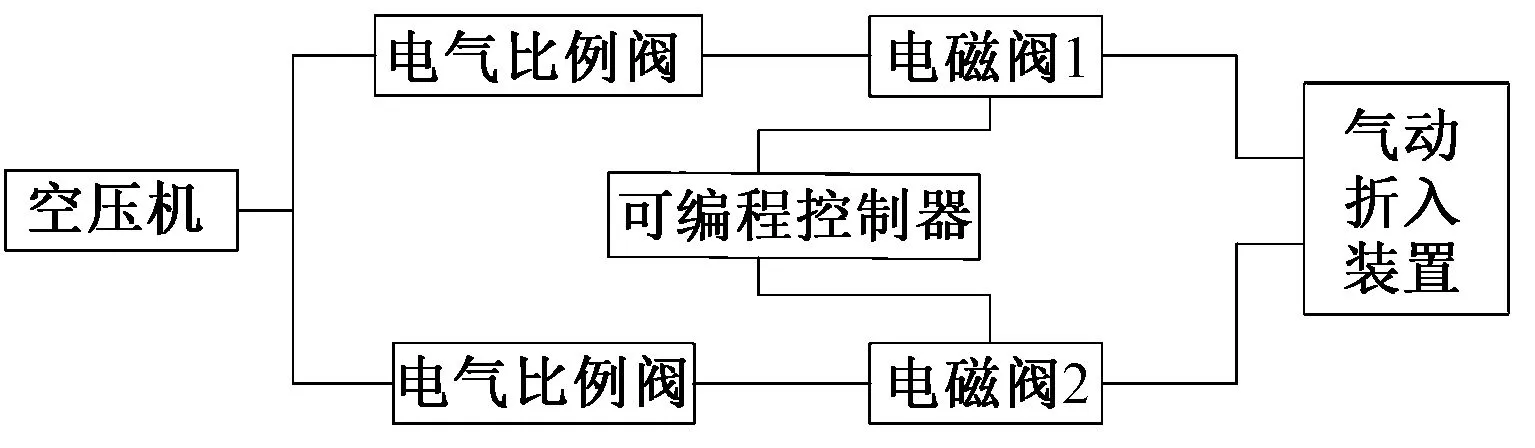
图2 气动折入装置实验平台Fig.2 Pneumatic tucking device experimental platform

2 数值模拟仿真结果及分析

为探究不同入射角度的斜吹气流对纱线折入的影响，本文将对入射角度分别为90°、60°、45°、30°的斜吹气流在相同工作条件下对纱线的影响进行探究。斜吹孔位置见图3，可以看出入射角度与纱线的对应位置。其中斜吹气流的入射压强为0.35 MPa，折入气流的入射压强为0.4 MPa，纱线线头长度为10 mm。

图3 斜吹孔位置Fig.3 Indication of oblique blow hole position

气流场中入射角为90°时不同时间步下纱线的运动状态见图4。

图4 气流场中入射角为90°时不同时间 步下纱线的运动状态Fig.4 Motion state of yarn in different time steps when incident angle is 90° in airflow field. (a)Time step 0.17 ms; (b) Time step 3.48 ms; (c) Time step 3.98 ms

从图4可以看出在每组仿真实验中选取0.17、3.48、3.98 ms时间步时纱线的运动状态，并进行相互对比。将其作二维坐标系定义：水平向左为X正方向；竖直向上为Y正方向。在设置纱线时忽略重力对纱线的作用，所以纱线开始时呈水平状态(X方向)，其左端固定右端自由以模拟纱线线头等待折入的状态。其中喷嘴口对纱线的相对位置固定，避免其因位置不同所引发的对仿真结果的影响。

气流场中入射角为60°时不同时间步下纱线的运动状态见图5。气流场中入射角为45°时不同时间步下纱线的运动状态见图6。

图5 气流场中入射角为60°时不同时间步 下纱线的运动状态Fig.5 Motion state of yarn in different time steps when incident angle is 60° in airflow field. (a)Time step 0.17 ms; (b) Time step 3.48 ms; (c) Time step 3.98 ms

从图5、6可以看出，气流首先从斜吹入口吹入，通过喷嘴管道射入大气环境，并作用于纱线上端。开始阶段有1个高压气团从喷嘴出口脱落附着于纱线与喷嘴口相对一侧。随着作用时间延长，纱线上端上侧高压区域由于对气流的阻挡作用，高压气团慢慢发展变大并随着纱线边线向着水平方向两侧延展。由于纱线上端高气压区的缓慢形成，与纱线下端的低气压区域形成压差，推动纱线向Y轴负方向运动。纱线在斜吹气流作用下，纱线上端从与Y轴垂直的状态向与X轴垂直状态移动。在斜吹气流作用下纱线运动到一定程度时，关闭斜吹气流，打开折入气流。此时纱线正对折入喷嘴的一侧，由于高速气流被纱线阻挡，在该侧形成了高压区，如图6(b)所示，高压区继续推动纱线朝着X轴负方向运动。在上述过程中，高压区域从纱线固定端向自由端缓慢移动，推动纱线运动直至折入状态，如图6(c)所示。综上所述，纱线折入主要依靠纱线两侧的压强差，高压气团随着纱线空间位置的改变进行移动并助推纱线更快地完成折入。

图6 气流场中入射角为45°时不同时间步下 纱线的运动状态Fig.6 Motion state of yarn in different time steps when incident angle is 45° in airflow field. (a)Time step 0.17 ms; (b) Time step 3.48 ms; (c) Time step 3.98 ms

气流场中入射角为30°时不同时间步下纱线的运动状态见图7，可以看出纱线在其余工况相同时30°斜吹气流作用下运动姿态的变化。

图7 气流场中入射角为30°时不同时间 步下纱线的运动状态Fig.7 Motion state of yarn in different time steps when incident angle is 30° in airflow field. (a)Time step 0.17 ms; (b) Time step 3.48 ms; (c) Time step 3.98 ms

在纱线斜吹和折入过程中，纱线由于高速气流的不稳定性均有晃动的情况发生，其不影响最终折入。仿真结果表明：在相同斜吹气流压强作用下，不同入射角度的斜吹气流对纱线有一定影响。纱线在不同斜吹气流作用下最终均能达到其斜吹气流喷嘴的角度。入射角为45°和30°相较于90°和60°，纱线在斜吹气流作用下的抖动情况显著减少，2组纱线在之后折入气流作用下的抖动也有所减少。其中45°入射角度的斜吹气流对减少纱线在气流场中的晃动效果最为显著，在后续折入气流作用在纱线的过程中，由于其初始位姿不同，纱线能更好地完成折入。由此可以看出，适当倾斜斜吹气流入射方向，即在竖直方向入射气流的作用下增加一定水平方向的气流，能显著减少纱线在气流场中的抖动现象，有助于纱线更好地完成折入。

3 实验结果及分析

通过对斜吹气流喷嘴位置的调整，研究不同入射角度对纱线折入的影响。由于本文平台很难达到30°入射角，且在实际工艺中过小的入射角会增大折入装置的体积和加工难度，过小的入射角也会导致在装置体积限制下喷嘴弯折程度的增加，加剧紊流的产生；故本文仅分别对90°、60°、45°斜吹角度的气动折入装置进行实验，纱线的运动状态如图8所示。斜吹角度为90°时纱线的运动状态见图8(a)，可以看出在不同时间步下实验中纱线的运动状态变化。由于只研究不同斜吹角度对纱线折入的影响，对折入气流的压强均设置为0.4 MPa；斜吹气流压强均设置为0.35 MPa；纱线线头(55 tex)长度选取10 mm。

图8 斜吹角度为90°、60°和45°时纱线的运动状态Fig.8 Motion state of yarn at 90°, 60° and 45° oblique blowing angle

用高速摄像机对斜吹气流入射角分别为90°、60°、45°时纱线的运动状态进行摄像，并对结果进行对比可知，3种状态下纱线均能完成折入。由于实验状态下纱线头端纤维丝的不规则导致各个实验组的纱线抖动情况均略大于仿真情况。其中斜吹气流入射角为90°实验组的纱线在斜吹过程中轻微抖动的程度最大，入射角为45°实验组的纱线抖动最小，入射角为60°实验组的纱线次之。实验结果和仿真实验结果基本吻合。

4 结 论

本文通过二维流固耦合数值模拟仿真和高速摄像实验相结合的方法研究了气动折入装置中不同入射角(90°、60°、45°、30°)的斜吹气流对纱线线头运动情况的影响规律，并通过对比分析优化气动折入装置的相关结构参数，得到如下结论：本气动折入实验装置中，10 mm长度的纱线线头在入射角为90°、60°和45°的斜吹气流作用下均能完成折入；适当减小斜吹气流入射角能提高纱线运动稳定性，使纱线更平稳地吹入梭口；通过数值模拟仿真和实验结果的对比分析，相较于入射角为90°和60°的斜吹气流，入射角度为45°的斜吹气流在纱线完成折入这一动作中的稳定性和可靠性较高。对斜吹喷嘴入射角的对比研究为气动折入装置斜吹喷嘴空间位置的设定提供了依据。