基于遗传算法及仿真技术的服装生产流水线平衡

黄珍珍，莫碧贤，温李红

(1. 闽江学院 服装与艺术工程学院，福建 福州 350108； 2. 福建省服装行业技术开发基地，福建 福州 350108； 3. 香港理工大学 纺织及服装学系，香港 999077； 4. 香港理工大学 深圳研究院，广东 深圳 518000)

服装生产线大都采用单件流生产线形式，生产流水线的平衡主要取决于流水线编排方案的合理性。服装流水线编排方案是根据生产任务，结合车间生产线情况，安排生产线内各加工设备的作业任务。合理的流水线编排方案可以缩短生产周期，节约生产成本，提高生产响应能力。在近几年的相关研究中，智能优化算法被较多地用于生产流水线编排。有研究采用遗传算法对生产流水线人员与工序进行一一指派以达到生产线平衡[1-2]，但是缺少与实际工位和平均生产节拍的结合；有研究结合工人熟练程度和环境等因素，采用蚁群算法分析服装生产流水线平衡问题[3]，虽算法本身具有分布式计算等优点，但涉及到的参数多，使得算法不是很容易确定合适的参数，计算相对复杂；有研究结合实际生产中的平均生产节拍和加工设备，采用粒子群算法解决服装流水线编制问题[4]，在流水线编制模型的约束条件中，对于工作地有3种不同作业性质的工序组合时，要适当增加该工作地总作业时间，以降低流水线因不同性质工序组合带来的误差；还有研究从仿真及评价指标方面对服装缝制流水线进行理论分析[5]，以及采用成组技术优化生产工序编排[6-7]。在这些研究中，智能优化算法的应用最多，证明了智能优化算法是解决服装生产流水线编排问题的一种有效方法。在调研童装企业生产流水线现状时发现，对于主要依靠经验型工人进行流水线编排的生产方式主要存在2个问题：一个是编制效率不稳定，时高时低；一个是投产前需要较长时间的生产流水线试运行以调试流水线的平衡。针对这2个问题，综合考虑企业实际生产情况，在关于用智能优化算法解决生产流水线平衡问题的现有研究基础上，本文先采用拓扑方法和遗传算法实现服装工序的自动优化编排，再采用仿真技术对编排方案进行单件流生产线仿真。以智能算法编排生产流水线，以仿真优化对流水线编排方案进行投产前平衡调试，可提高编排方案的编制效率，缩短编排方案的调试时间，促进传统生产方式向数字化生产方式转型。

1 服装生产流水线的平衡

1.1 问题描述

本文选择某中大型童装企业的生产流水线为调研对象，该企业的订单生产数量较大，生产的款式种类较多。通过实地调研发现，企业基本实现了吊挂单件流生产线模式，在所调研的车间中总共有15条生产流水线，工艺设备较好，空间配置能力高。一般在生产大货之前，企业先对服装工序及工时进行分析，由经验丰富的技术人员根据工人的工艺水平初步将各个工序分配到生产流水相应的设备上，为使生产流水线达到相对平衡，需要在流水线上试运行3 d左右，在试运行期间对不合理的工序和人员进行调整，直到流水线能顺畅地运行。从最近生产的大量订单中挑选出具有一定代表性的童装款式，包括连衣裙、单裤、上衣等近20余款，分析得到的生产数据显示，这些服装款式的生产线编制效率基本在50%～70%之间，最低的编制效率只有42.1%，最高的编制效率为78%。该企业的订单生产数量少则几千件多则上万件，如果能提高生产线编制效率，缩短产前生产线平衡的调试时间，企业的产品生产周期将大大缩短，生产响应速度也随之相应提高。企业若是解决了生产流水线平衡存在的主要问题，借助企业相对先进的吊挂生产设备，那么企业在生产环节上的数字化智能生产和管理水平都会得到一定程度的提升。

针对该企业的单件流生产线作业方式，分析近20余款童装的生产流水线编排方案，归纳为如下问题：一件童装成衣的缝制是由若干工序按照一定的加工顺序完成，每道工序具有一定的标准时间和加工设备，将这些工序分配到一定数量的工位上加工，那么在不改变加工顺序以及每个工位上的设备尽量一致的约束条件下，如何将这些工序进行指派使其在要求的工位数上按照单件流水形式最均衡地完成整个缝制工作，这是一个较为典型的非确定性多项式(简称NP-hard)难题。

1.2 流水线的平衡优化算法

通过以上问题描述和相关的智能优化算法研究得知，在进行智能优化算法设计时，如果实际生产的约束条件过多，会增加算法设计的难度，确定合适参数的难度也相应增加，也有可能会导致算法易陷入局部最优。由于影响服装生产作业的因素较多，如工人的技术水平、浮余时间、工厂的作业环境以及加工设备的先进程度等等，分析这些因素对生产流水线平衡的影响权重，将其分为主要决定性影响因素和次要决定性影响因素。主要决定性影响因素是工序的加工顺序、平均生产节拍、加工工位数以及加工设备；次要决定性因素为工人技术水平、浮余时间、在制品传递时间等等[8]。为了降低算法设计的难度以及增加算法运算的准确度，将主要决定性影响因素作为约束条件与遗传算法相结合，在MatLab(R2016b)中建立生产工序自动编排模型；将次要决定性影响因素作为仿真的约束条件，在Plant Simulation仿真软件中进行流水线编排方案的生产仿真，优化流水线编排方案，使其可以适用于实际的批量投产，从而找到一种解决生产流水线平衡问题的方法。

1.2.1 生产工序自动编排数学模型

根据以上问题描述，建立单件流生产线数学模型。企业大都采用单件流生产线，设1条吊挂流水线为1个加工单元，该加工单元由W个加工工位，N个作业工人组成。设1个订单款式为1个加工任务P，它由k道工序完成，Pi表示加工任务P的第i道工序。设ti表示工序Pi的标准工时，Mi表示工序Pi对应的加工设备[9]。本文的模型有以下假设：

1)在制品的传递时间可以在流水仿真中进行设置，在此模型中不予考虑；

2)工人的熟练程度可以通过岗前培训进行训练，熟练程度差异可以在流水仿真中作为浮余时间进行设置，在此模型中不予考虑；

3)W为加工单元上用于加工的总工位数；

4)已知每道工序的标准工时和加工设备，并且工序的作业排序不可改变；

5)工序组合过程中，加工设备不同的工序尽量不组合在一起，为便于设备排布，同一个工位最多布置2种加工设备。

平均生产节拍SPT的计算公式为

(1)

储备站加工数量的计算公式为

(2)

式中：Qf为储备站加工数量，件；tj为工位j的加工总时间，s；Q为生产线总的加工件数。

在评价服装流水线平衡问题时，常用编制效率和均衡指数2个评价指标。编制效率η的定义为

(3)

在遗传算法模型设计中，优先采用均衡指数St作为生产流水线平衡的优化目标函数:

(4)

1.2.2 算法实现与步骤

根据以上数学模型，为满足模型的约束条件，将拓扑方法以及优化目标函数应用在遗传算法中实现工序的自动优化编排。遗传算法是一种比较成熟的智能算法，通用性强，具有鲁棒性和随机全局搜索能力，能以极大的概率找到全局最优解，适合并行分布处理，并且计算过程简单。拓扑方法能简单有效地解决工序的作业排序问题；优化目标函数能对平衡率和加工设备分布都进行最优处理。因为工序自动编排模型是基于主要决定性影响因素建立的，所以自动计算得出的结果能决定生产流水的整体平衡性和优化性，但对一些次要决定性影响因素[10]，需在Plant Simulation仿真软件进行生产流水线仿真运行时考虑，增加实际生产条件的设置，更直观地模拟实际生产。Plant Simulation仿真软件在工厂和生产线的建模、仿真和优化生产系统等方面，可以创建广泛的统计数据和图表来支持对生产线工作负荷、设备故障、空闲与维修时间、关键性能等参数的动态分析，从而能将次要决定性因素和人工经验很好地结合，预防生产流水线的不合理问题，大大缩短产品的生产周期，直观地再优化生产流水线平衡，解决工序编排方案过于理论化问题[11]。

根据以上优化思想和算法，得到生产流水线平衡优化算法的流程图，如图1所示。

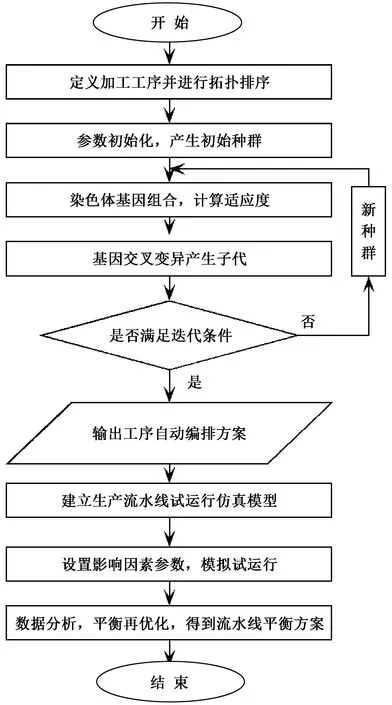
图1 服装生产流水线平衡算法流程Fig.1 Optimization algorithm for garment production line balance

平衡优化算法的主要步骤如下：

步骤1，根据工序流程图定义每道工序的标准工时和加工设备，对工序进行拓扑排序。

步骤2，加工单元工位数、初始种群以及交叉变异概率等参数的初始化设置，随机产生初始种群。

步骤3，根据生产流水线平均节拍，将初始种群中的工序进行组合作为染色体中新的基因；结合工位上加工设备尽量一致的约束条件，计算种群中各个染色体的适应度值，适应度函数为f(St)=1/St。

步骤4，根据交叉概率对染色体基因进行交叉，再根据拓扑排序对基因进行变异，得到子代，将子代中适应度较好的染色体作为新的父代选择到种群中。

图3 连衣裙工序流程图Fig.3 Flowchart for skirt manufacturing

步骤5，重复步骤3、4，直到满足迭代条件为止。

步骤6，选取适应度最大且加工设备约束最优的工序编排方案。

步骤7，根据工序编排方案，在Plant Simulation仿真软件中，采用串并联的方式将各个工位按照实际生产流程，建立单件流生产线仿真模型。

步骤8，在仿真模型中，进行在制品传递时间以及生产总数量等实际生产参数的设置，生产流水线动态仿真运行。

步骤9，分析生产流水线仿真运行数据，结合生产环境和人工经验进行生产流水线再优化，得到优化后的生产流水线编排方案。

2 生产实例应用

2.1 童装生产流程图

以所调研童装企业中的连衣裙生产为例，其款式图如图2所示，工序流程图如图3所示。总生产数量为46 806件。以其中1条生产线为例，该线实际生产数量为4 000件，目标日产量为850件/d，人均台产量为3件/h，线上加工工序为23个，编制效率为78%；线外加工工序为4个，线外加工工序为图3中的10号、11号、12号、14号工序。

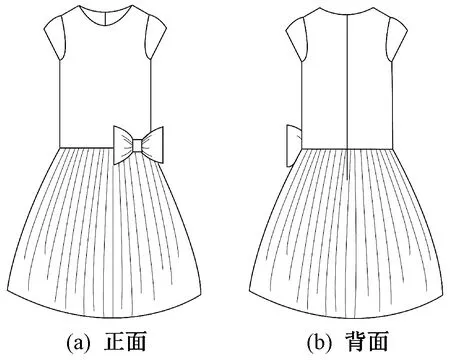
图2 连衣裙款式图Fig.2 Dress sketch. (a) Front details; (b) Back details

2.2 生产工序自动编排方案的生成

在MatLab优化模型中，为了能给实际应用带来灵活性，模型可以根据实际生产需要自行设置加工工位数W(W大于或等于最小工位数)，再根据工序流程图中显示的工序相关信息，输入工序的加工设备M={M1,M2，…,M26}，工序的标准工时t=[t1,t2, …,t26]。根据式(1)，模型可以自动计算得出流水线的平均节拍，在平均节拍和加工设备的约束条件下，还可自动计算出当前工位数的优化工序编排方案。同时，模型也可以根据需求设置不同工位数，得到不同的工序编排方案，再分别对其进行生产仿真，选择出最适合的生产流水线编排方案，增加了方案的选择性。本文仅以1个工序编排方案为例来说明方案的自动生成和仿真优化。以输入工位数12为例，运行程序，得到工序编排方案，见图4。

由工序编排方案可以看出，方案总体上实现了生产流水线平衡和加工设备的最优约束，但是还需要在仿真软件中进行生产环境等次要决定性因素的设置，以还原真实生产环境，优化工序编排方案，达到生产流水线的平衡优化。首先，结合在制品传递时间、工位设备现场布置等现实因素，将使用同种加工设备的工序2和工序17合在一起进行生产，降低设备排布难度；将工序18～26整体指派给工位J、K、L进行加工，降低工位节拍[12]。调整后的工序编排方案见表1。由此，首先在Plant Simulation软件中进行生产流水线建模，由于工位I相对闲置，因此设置1个储备站，用于工位I利用闲置时间分流后3个工位的加工作业，整个生产流水线仿真模型见图5。

图4 工序编排方案Fig.4 Workstation scheduling

表1 调整后工序编排方案表Tab.1 Restructured workstation scheduling

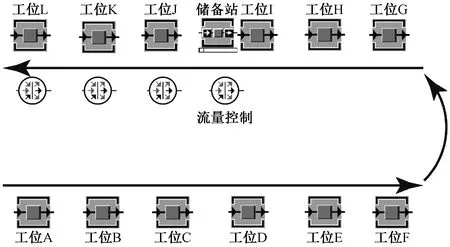
图5 生产流水线仿真模型Fig.5 Simulation model for production flow

然后，在每个工位模型中设置工序参数以及工位分流参数。在源工位设置该生产线实际生产数量为4 000件,代表加工单元物料的进入数量。在储备站分流设置时，根据式(1)计算得出平均生产节拍SPT为98.88 s，从而计算得出工位I的闲置时间为39.97 s，再由式(2)计算得出储备站最大分流生产数量为436件。对源工位、工序返修率、生产工位以及各工位之间物料流动方式、物料终结工位进行参数设置，对模型进行生产流水线的仿真运行，得到完成生产总数量的生产流水线仿真运行情况，结果如图6所示。从流水线仿真运行数据中可以得出，经工位I分流之后，J、K、L这3个工位的平均生产节拍由原来的122.18 s降为108.8 s，图7示出每个工位上的生产节拍。由式(3)计算得出，经过仿真优化之后的生产流水线编制效率提高至90.8%。

图6 生产流水线仿真动态图Fig.6 Dynamic chart for production flow simulation

图7 各工位生产节拍Fig.7 Pitch time of work stations

2.3 生产流水试运行结果

通过生产工序自动编排到生产流水线仿真优化，以上实例的线下加工工位减少，编制效率达到90.8%，比原编制效率提高了12.8%；并且该生产流水线平衡优化方法的计算时间短，在一定程度上缩短了生产周期。

3 结束语

通过理论分析和实例验证，针对单件流生产线作业形式，将遗传算法与仿真技术相结合的方法可以有效地平衡优化服装生产流水线。在算法设计中，采用拓扑方法和遗传算法，考虑影响生产流水线平衡的主要决定性因素，实现工序自动编排，达到编排方案的初步优化，同时结合实际生产条件和生产经验，采用仿真技术平衡生产流水线，符合实际生产需求。这种方法在一定程度上降低了智能优化算法在解决非确定性多项式问题时各种参数和约束条件的设置难度；同时，从仿真实验中总结流水线仿真的影响因素和方法，可为后期工作中开发服装生产流水线优化仿真系统提供一种研究思路。