多智能体博弈的纺织车间搬运机器人任务分配

李 珣，南恺恺，赵征凡，王晓华，景军锋

(1. 西安工程大学 电子信息学院，陕西 西安 710048； 2. 工业和信息化部 电子第五研究所，广东 广州 510610)

无人化、智能化的生产加工环境是近年纺织产业升级的主流方向，因此，将机器人设置在生产环节中替代一部分简单的人力工作是纺织企业所采用的初步升级方式。对于纺织产品生产的基本单元车间而言，特别是纺织车间的棉卷搬运，以及某一特定棉卷装卸需求，存在时间上的连续性和状态上的离散性特征，所以需要多个移动机器人协作完成，但是，当大量的机器人出现在生产现场，各机器人之间的对抗关系会显著增加，系统生产效率会大大减小；因此，将机器人个体间的信息与资源共享，对多机器人系统进行智能化改造，能够互补机器人状态未知造成的任务完成时间断续、累积，提升系统的鲁棒性和容错能力。多机器人智能系统中，多任务的分配方案最优化，是保障整体工作有序完成的基本条件，同时也是提高生产效率和降低机器人使用成本的前提。

当前多机器人任务分配的研究尚未有直接应用在纺织制造领域的研究方案，但针对其他不同的应用场景，国内外学者提出了诸多卓有成效的任务分配实现方法[1-2]。从宏观上主要可划分为集中式和分布式2类。集中式的任务分配，如多维旅行商模型[3]、多维动态网络流优化模型[4]，能够得到在静态环境中的任务分配最优解。随着计算机运行能力的提升和机器人个体智能化发展的需求，分布式的任务分配方法已成为主流的研究方向。其中，基于行为的分配方法，如Tang等[5]提出了一种基于启发式搜索的多机器人系统任务分配算法，实现了异构多机器人系统中的任务分配。虽然实时性和鲁棒性较好，但是不能获得全局最优解。市场机制的任务分配方法[6-7]是基于市场经济的原则，在求解过程中充分考虑各个平台间的信息交互和协商：如段俊花等[8]提出的基于视觉的阈值模型和基于通信的显式协商协调机制相结合的多模态融合算法，解决了多机器人对未知区域有害废弃物的清理问题；齐心跃等[9]提出的基于市场机制的多机器人救火任务分配策略，能较好地实现不同工况下动态分布式任务的分配。但该类方法工作时各系统独立运行，应变能力较差，通信成本高，当网络通信较差时，系统性能将大大降低。

基于多智能体的任务分配算法[10]能够较好解决未知环境中多机器人的自组织任务分配问题，且具有随机性，任务探索范围广，对于动态的任务分配适应性强。秦新立等[11]提出的改进蚁群算法，实现了发电厂清洁机器人对太阳能电池板清洁工作的任务分配；刘淑华等[12]针对大规模多机器人系统中任务的紧密耦合性，采用了层次结构，分别使用基于蚁群、粒子群蚁群和量子蚁群实现机器人集合，产生紧密耦合型任务解；Fang等[13]考虑到情感对行为和决策自主性和多样化的影响，将情绪感染引入到机器人任务分配中，提出了一种基于情感传染的寻踪任务分配算法(PTA-EC)，该算法描述了机器人之间情感的相互影响对任务分配的积极影响。但这些算法收敛速度较慢且易陷入局部极值。近年来，借鉴经济学中的博弈论[14]，将其进行启发式改进应用于任务分配中，较好地解决了上述智能体在资源分配中存在的问题。

综上，现有多机器人系统中任务分配研究，多以分布式方法解决非特定环境下的任务分配，基于启发式的智能算法在面向特定环境下的任务分配的解决上已初现优势。本文通过调研相关纺织企业，根据当前纺织厂所存在的提高车间物料调度效率、减少人工成本等问题，针对具体的棉卷搬运过程：多任务、多机器人、分配任务随机等复杂动态任务分配问题，以及任务分配过程中的个体间的冲突、化解的最优化问题，根据实际生产空间、时间、效率等限制，进行了针对多机器人多任务分配模型和优化算法的研究。引入博弈论思想,并进行启发式改进，提出基于智能体博弈理论分布式自主决策框架，在该决策框架下任务的分配能够得到全局最优解，具有较强的可扩展性、良好的鲁棒性与收敛性能和合理的分配结果。

1 纺织车间物理环境及任务描述

1.1 纺织车间物理环境及智能体抽象描述

1.1.1 车间物理环境及机器人状态

图1 精梳车间工艺流程图Fig.1 Process flow chart of combing workshop

由于传统的人工上料存在这些较长的延误时间，大大影响车间生产效率，因此，本文从消除以上时间延误着手对精梳车间智能化改造，将实际车间生产环境构造为多机器人随机分布的精梳机车间示意图，如图2所示。每个机器人只有负载1个棉卷的能力，只要并条机某一工位有任务需求则机器人就能够响应，使得各工位之间独立运行，换料时间互不等待。针对工序特征，将每个工作点位独立作为供料对象，存在条并卷机8台，工作点位8个/台，充电位1个，棉卷供给机1台，替代人工的机器人若干。

图2 纺织车间生产任务抽象简化示意图Fig.2 Abstract description and simplified schematic of textile workshop production task. (a)Combing workshop; (b) Machine distribution in combing workshop; (c) Simplified task abstraction diagram of workshop

1.1.2 智能体及任务抽象描述

由于多任务的完成需要智能体具有彼此合作、协调和谈判的能力，移动机器人需要进行自身判断和信息共享，所以将搬运机器人抽象成一个具有简单逻辑判断的智能体Agent。同时，由于从精梳机上下料的棉卷在厚度上存在一定的差异，并且任意2个并条机的不同工作点在工作完成时间上不同步，所以对于顺序执行和分配仅存在于车间内机器首次开车工作时。本文研究内容是针对正常生产需求时的多任务分配工作，任务与机器人状态均为随机，因此，纺织车间棉卷搬运任务分配问题是一个动态决策问题，从实现的角度来看，可以看作是3个基本对象：时间、任务环境状态信息和智能体之间的交互，该问题符合在时间上迭代求解[15]。将具体的纺织生产过程中的任务环境进行抽象简化，如图2(c)所示。图中：方框表示生产工位；T1～Tn代表存在n个任务需求(即任务分布情况)；圆点表示具有简单思维判断的智能移动机器人。

综上，以现实需求的场景为例：当某时刻、某工位处有任务执行需求(装载/卸载)，则会向分布在工位周边的多个智能体发出任务请求，智能体根据自身状态进行应答。为完备智能体工作环境，根据生产环境对任务分配研究背景进行以下假设。

1) 任务环境地图已知，以某精梳车间为例，如图2(b)所示，任务位置和智能体位置存在于已知的环境地图中，即本文中智能体在获得任务分配时不需要考虑创建环境地图。

2) 智能体移动范围有界，由于生产车间通信和场地范围限制，智能体仅于有界范围内移动。

3) 智能体任务获得过程不存在复杂障碍物的干扰，无人化生产环境，除生产设备和工作机器人自身的相互位置冲突外，无其他突发障碍物对智能体的任务获得过程造成干扰。

4) 智能体的运动路径不受约束，实际生产对象为非循迹机器人，智能体在任务分配过程中自主决策，路径除受固定设备约束外不受随机障碍约束。

5) 智能体与任务之间的强通信连接，智能体能够实时获取与发送任务需求与自身状态。

6) 智能体移动速度相同，考虑实际工作中所有的搬运机器人是同构的，则要求智能体的运动速度恒定且相同，仅在启停时存在加速度和减速度。

7) 智能体预知的信息：每个智能体实时获取自身的状态StateAj，通信获知其余智能体状态，以及该智能体当前时刻可选择的某个任务Ti。

1.2 基本任务分配

1.2.1 静态任务分配

静态任务主要出现在系统第1次上线情况，即在任务分配初始时刻所有工位均处于未分配状态，智能体处于空闲状态；或是车间中某台机器进行检修，首次加入到车间生产系统中时，该并条机整机工位均处于未分配状态。则任务分配决策过程中，每个智能体根据目标函数值，选择最适合自己的任务，如果有智能体选择了相同的任务，则它们之间呈现协作关系。任务执行时，由于每个智能机器人被认为单独完成任务的能力有限，因此，每个智能体在时刻t只能选择1个任务T执行，每个任务需要由多个智能体协作且智能体处于空闲状态才能响应任务的请求。

1.2.2 动态任务智能体响应

在实际生产中存在动态情况发生时，定义动态情况为系统中某一时刻t有新任务的产生或任务丢失事件发生时，环境的动态变化会导致任务完成的代价发生变化，从而导致目标函数值的变化，故系统需要根据智能体的能力约束和目标值，尽量在不改变原期望结果的情况下快速寻找最优调整策略。这就要求将1组任务分配给1组机器人的同时，要将能力约束与任务调度结合起来，在约束条件中建立和时间有关的目标函数找到1组任务的最优分配给1个智能体子集，该子集将负责完成任务。

2 基于博弈理论多任务分配模型

在对纺织生产过程中的机器人基本任务类型归类的基础上，针对车间任务类型简单，任务数量较大的特点，依据多智能体和多任务间“多对多”的协作关系、扰动关系，首先需要分别对智能体和任务状态建立数学模型；其次，对于任务和资源的时间上连续，状态离散特征，借助复杂博弈论对此类问题进行建模，已被证明较其他方法具有先进性[16]。因此，本文针对特定环境下的任务分配，根据任务和对象特点，对复杂博弈论根据文中优化决策对象进行启发式算法改进，建立多任务分配模型，解决纺织车间多智能体任务分配问题。

2.1 博弈理论

2.2 纺织车间多任务智能体基本模型

借助博弈理论中个体博弈以及Nash均衡的描述，同时结合1.2节中车间任务需求和智能体的任务状态，对任务与智能体进行模型建立。

2.2.1 物理集合

(1)

执行任务Ti,智能体所需代价为Pi，代价矩阵为

Pn×m=(bi,j)

(2)

式中，bi,j表示任务Ti与智能体Aj之间的欧氏距离，距离越远，代价越高。

物理集合中，本文根据任务等待时间确定了任务的优先级，将任务优先级转化为任务收益；根据任务与智能体之间的物理距离确定了每个智能体对应不同任务的代价矩阵。

2.2.2 工位任务状态

2.2.3 智能体状态

在t时刻智能体Aj的状态用函数StateAj(t)=〈posj(t),ej(t),vj,q(t)〉描述。其中，posj(t)为智能体Aj在t时刻的位置信息；ej(t)为智能体Aj在t时刻相应的能量存储值；vj为智能体Aj的速度值；q(t)为t时刻的智能体Aj任务分配状态矩阵。

(3)

qi,j(t)=1表示t时刻将目标任务Ti分配给智能体Aj；qi,j(t)=0表示未将任务Ti分配给Aj，即智能体Aj处于空闲状态。智能体间信息交互能力用con表示，为n×n矩阵，其元素conij表示智能体之间的通信网络连接强度，conij=k。k∈[0,1]，其中1表示强连接，0表示无连接。同时，t时刻智能体Aj完成任务Ti的能力用式(4)表示：

capi,j(t)=ej(t)-FPi

(4)

式中：F是阻力常量；Pi是执行任务Ti所需的距离代价。任务分配映射关系：T×A⟹{S1,S2,…,Si}，Si是对任务Ti特定的任务集合。

2.2.4 目标函数

本文中对某一时刻进行多任务分配的目的，是计算该时刻多个任务机器人完成收益，并寻找到全局收益最大化的分配，根据式(1)和(2)，要求该时刻机器人全局消耗最优，任务收益最大。即本文中智能体获得任务后保留最大能量存储和最大任务收益，因此认为系统目标函数是整个智能体个体能力与收益的总和。目标效用函数的定义如下：

(5)

(Ti,l)表示对完成任务Ti所形成的智能体集合。

上式满足条件：

dij∈{0,1}, ∀Ti∈T, ∀Aj∈A

(6)

这里的dij是智能体的二进制决策变量，指是否将执行任务Ti。

2.3 多智能体博弈的任务分配算法

以往在完全连接的网络中，在每次迭代中只选择1个智能体(领导者)来做出决策，而本文中提出的分布式的决策算法，将纺织车间搬运机器人任务分配问题转化为一个博弈事件，建立一个针对特定任务无需领导机制的智能体集合决策框架，当有任务需求时，其中每个智能体会根据自己的状态StateAj(t)加入一个集合。

2) Nash稳定性分区的建立：对智能体建立不相交分区∏={S1,S2,…,Si}，如果对于任意一个智能体Aj∈A，存在maxA(T∏(j),|S∏(j)|)≥maxA(Ti,|Si∪{Aj}|),∀Si∈∏。则称这个分区∏是Nash稳定的。即在Nash稳定分区中，与其他任何集合相比，每个智能体都更倾向于其当前所在的集合。每个智能体在该分区内无需任何形式的信息和通信技术，任何智能体不得单方面偏离其目前的决定，系统保持一种稳定状态。

3) 决策结果：在智能体寻找强偏好任务的决策过程中Nash均衡理论决定任务的最终分配结果。Nash稳定分区一旦建立，任意一个智能体都不可能在其他智能体任务完成策略不变时，单方面改变任务完成策略增加其整体收益，即对任务目标生成了一种最优策略组合。

4) 对不确定性问题的适应：本文将纺织车间多机器人系统的不确定性主要归结为机器的机械故障、搬运机器人的动作输出故障、噪声所造成的通信的不确定性和传感器的不确定性。当前主要考虑车间环境下的多任务分配问题，在任务分配过程中智能体只对任务需求作响应，即任务层面的协调，而不考虑多机器人运动控制层面的协同，所以搬运机器人动作输出的不确定性和传感器所造成的运动上的不确定性不在本文考虑范围；机械故障所造成的工位停工，任务需求中止，属于任务动态的发生；另外由于任务分配很难保证每个智能体之间能够强通信连接，因此将噪声所造成的通信的不确定性和传感器信息感知的不确定性归结为通信失效，而针对通信失效的问题，本文多智能体博弈的分布式智能算法中，以局部信息广播的形式做个体信息的交互，对通信具备很好的自适应能力，具体在模型中体现为每个智能体只需根据自己的目标效用函数maxA选择加入一个任务分区∏，只需将自己的决策状态dij广播出去，而其他智能体只根据自身所获得的局部信息State(t)做出决策，并同时影响其相邻智能体。决策实现的算法流程如图3所示。

图3 算法流程图Fig.3 Algorithm flow chart

3 实验结果与分析

3.1 实验环境及数据初始化

1) 实验环境描述。根据实际生产需求，本文实验中的任务为紧耦合型任务，即每个任务的完成需要多个智能体的合作，要求将m个智能体合理地分配给n个工位的任务，任务的分配决策过程应该由智能体以分布式、自组织的方式完成。

从分析结果可以看出，电机的温度分布中，最高温度产生在绕组部位为130℃。对于一般电机来说完全不是问题，也就是说该电机完全可以满足长时工作的需求。

2) 数据初始化及实验流程。本实验在MatLab R2016a上实现。实验结果如图4所示，图中X,Y为伪坐标，用于描述智能体位置之间的相互关系。

图4 任务分配迭代完成过程Fig.4 Iterative completion process of task allocation. (a) Iteration 79th; (b) Iteration 139th; (c) Iteration 189th; (d) Iteration 331th; (e) Iteration 597th; (f) Iteration 682th; (g) Iteration 771th; (h) Iteration 804th

图4示出用于任务(n=6)分配的多个智能体(m=60)的分布式决策过程，任务分布在1 000×1 000的范围，智能体分布在800×800的范围。图中，圆表示智能体，正方形则表示任务，圆之间的线代表智能体的通信网络。为了直观，本文任务分配结果根据颜色的区分将有色智能体被分配给相同颜色的任务，例如黄色智能体(图中黄点)属于执行黄色任务(黄色方框对应任务t4)的集合。如图4(a)中,初始时刻智能体针对任务需求决策处于随机状态，随着时间的推移，算法迭代，智能体之间以局部交互的方式做出对任务的临时决策(迭代过程如图4中(b)～(g)所示)。最终如图4(h)所示，经过804次算法迭代之后，各智能体集合形成Nash稳定分区，系统得到稳定的决策结果。

3) 实验结果及分析。为验证本文算法针对不同任务的完成效率，首先进行了弱通信网络强度下不同任务需求数量的任务分配结果比较，完成了智能体个数m=60,任务个数分别为n=5,6,7,8状态下的任务分配。以算法迭代次数作为性能评价依据，实验结果如图5所示。

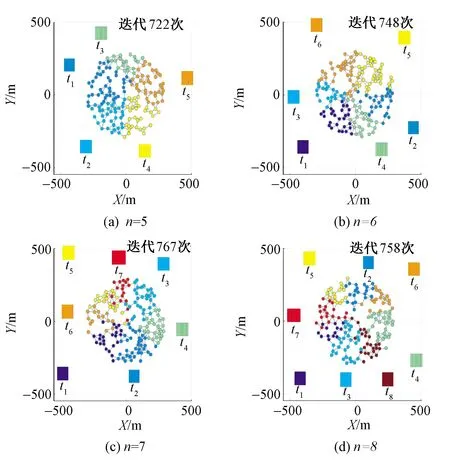
图5 相同数量智能体在不同任务数量下的完成结果Fig.5 Results of the same quantity of agents in different task quantities

在相同执行智能体数量下，任务数n=5,6,7,8时任务分配完成算法迭代次数分别为722、748、767、758。可以看出，在弱通信网络强度状态下任务的增加对本文任务分配决策的完成效率影响并不显著。

本文任务分配算法在强通信网络强度下，分别取任务数n=4,5,6,7,8的不同数量级智能体的任务分配完成性能实验，结果如表1所示。

针对紧耦合型任务中智能体数量m略多于任务数量n时算法均能快速迭代完成分配。在表1结果中观察每一行实验数据，不论智能体数量m的值取多少，任务数n=4,5,6,7,8算法迭代结果比较接近，不存在明显异常情况，那么同样可以得到如前述结果，即本文算法在同一数量级智能体情况下，每一行中任务的增加对决策的完成效率影响并不显著。

从表1数据还可看出，随着智能体数量的增加，算法中智能体需要更多的信息交互，因此算法迭代次数也会如表1结果所示随之增加。当n=4，m=120时；n=5,m=130时；n=6,7,8,m=135时，在有限的空间内智能体数量达到饱和，此时当智能体数量继续增加，算法无法完成任务的分配。

3.2 对比实验

表1 不同数量级m,n下算法迭代性能结果Tab.1 Iterative performance results of algorithms under different order of magnitude m and n

图6 3种不同方法的任务分配收益情况Fig.6 Task allocation income of three different methods

从实验结果可以看出，在任务完成的总收益值上本文特定模型下的多智能体博弈任务分配算法具有明显优势，本文算法的任务总收益值明显高于文献[9]基于市场法的任务分配算法，略高于文献[14]中救火任务模型中的空闲型实验。这是由于市场法中参加招标的智能体并不能保证其他个体选择与其相同的任务策略，个体之间存在竞争和干扰关系，因此需要更多的迭代次数算法才能达到收敛，系统获得的收益值较少。而文献[14]所提出的救火模型不仅计算其自身的最优效用函数，还计算其他可能参与合作灭火的机器人的效用函数，虽然获得的总收益高于市场法，与本文算法收益值接近，但是需要更多的计算，且算法在迭代65次之后才能达到稳定状态；而本文算法能够在保证获得稳定的高收益值的情况下，仅需要迭代45次即可得到稳定的分配结果，因此，本文算法在紧耦合型任务分配中的系统收益和分配效率明显优于另外2种算法。

3.3 动态任务决策能力和系统扩展性分析

在实际生产加工环境中，存在大功率电动机等强电磁干扰，任务信号的丢失与干扰信号的出现也是本文算法需要考虑的问题，因此，对提出的决策框架进行了动态环境扰动实验，如意外的任务添加或丢失。以m=15,n=10进行实验。算法在第1阶段迭代45次后完成分配决策获得稳定收益，本文设置了在a点处随机丢失1个任务，b点处增加该任务，结果如图7所示。

图7 任务发生动态变化时系统收益Fig.7 System benefits in dynamic task change

本文算法在迭代105次时随机丢失1个任务，此时系统收益值明显下降，但是依旧能够达到稳定状态，当稳定状态持续一段时间后又增加该任务，算法仍能快速收敛获得稳定收益。这是因为智能体博弈过程中能够根据自身收益决定对任务的偏好关系，快速组成新的任务集合收敛到Nash稳定分区，可以响应于任何动态任务环境变化。

为验证本文所述算法对通信网络动态环境的鲁棒性，以相同数量的智能体和任务对不同网络通信情况下的任务分配效率进行比较，实验结果如图8所示。图8(a)为强通信连接；图8(b)为通信失效30%的弱通信连接。

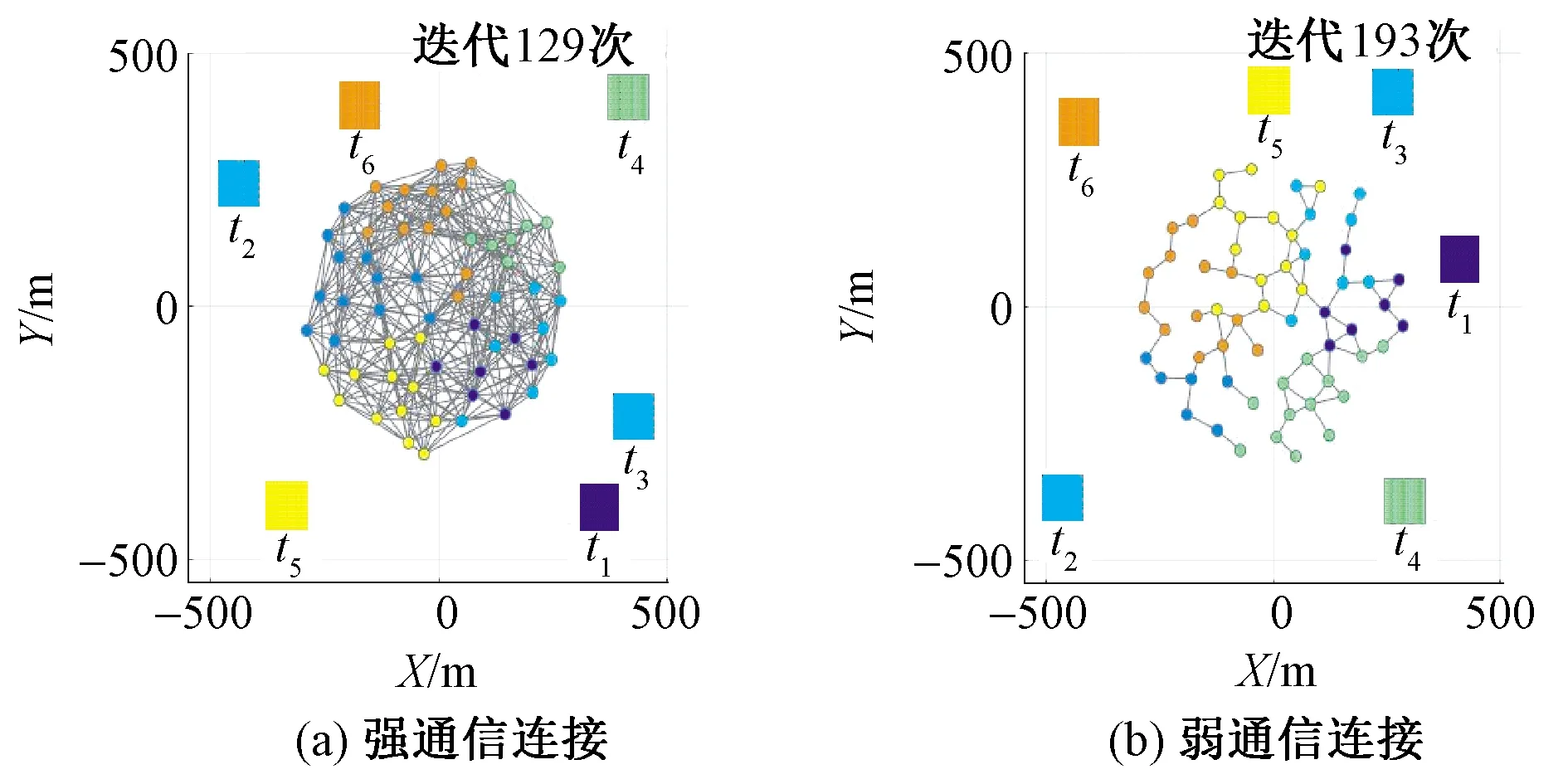
图8 不同通信网络强度下的任务分配结果Fig.8 Task allocation results under different communication network strength. (a) Strong communication; (b) Weak communication

当智能体之间的通信网络是强连接时，本文的分布式决策算法能够快速完成129次迭代，达到良好的任务分配结果。以同一实验对象，在智能体弱通信网络情况下，通过193次算法迭代完成分配，虽然在弱通信网络连接下算法迭代次数多于强通信网络下，但同样具有良好的任务分配结果表现。

为进一步探讨本文算法的鲁棒性，实验对本文算法和常见的基于粒子群算法(PSO)及基于市场法的任务分配，在无通信失效的强网络连接和通信失效30%的弱通信网络进行任务数为6，不同数量级智能体任务完成时间比较，实验结果如表2、3所示。

表2 强通信网络连接实验结果Tab.2 Experimental results of strong communication network connection

表3 通信失效30%的弱通信网络连接实验结果Tab.3 Test results of weak communication network connection with 30% communication failure

从表2、3结果可以看出，通信部分失效使得系统完成任务的时间均有所增加。在强通信网络下，市场法优于PSO算法，但收敛速度不及本文算法。在弱通信的情况下，本文算法能更快地收敛，找到最优的任务分配方案，此时PSO算法的鲁棒性较优于市场法。这是由于基于市场机制的任务分配算法本身应变能力较差，而且对通信成本要求很大，当网络通信较差时，系统性能大大降低，任务分配完成时间受通信失效的影响较大；而PSO算法由于粒子之间不需要全连接，所以通信鲁棒性较好。但粒子随机运动中允许不可行解的存在，因此存在部分死锁解的情况，而死锁解的存在使得PSO解空间减小，因而全局寻优能力受到影响，在强通信连接下收敛较慢。而本文博弈论中在Nash稳定性区间建立过程中个体以自身收益值作为目标函数的关联度，进行局部的广播式的信息交互使得该决策框架对通信部分失效具有很好的鲁棒性，同时在相同的任务环境下，博弈论任务完成时间明显优于PSO和市场法，因此，本文的多智能体博弈的任务分配算法更适合于纺织车间这种环境复杂、通信覆盖不稳定、对任务分配完成时间有严格限制的实际生产场合。

为验证该任务分配决策框架的可扩展性和大规模任务分配的效率，分别取5～8个任务，采用大规模智能体群体做实验验证，分别针对不同任务以165～210个智能体作为实验对象，实验结果如图9所示。

图9 不同情况下任务分配实验Fig.9 Task allocation experiments under different conditions. (a) Allocation of efficiency in different situations; (b) Isometric map for allocation efficiency

对比发现，任务分配的完成效率和智能体的数量相关性较强，随着智能体数量的增加，任务完成的迭代次数呈现正相关性。而任务数量的增加对迭代次数的影响较为微弱，在图9(b)等高线图中呈现出清晰的分布和均匀的过渡，所以该任务分配决策框架不论在任务还是智能体上均表现出良好的扩展性能。

4 结束语

本文将多智能体博弈论的思想引入纺织服装生产过程中搬运机器人的任务分配决策中，将移动机器人定义为能够独立思考的智能体，智能体间各自通过局部状态信息的交互，追求利益的最大化，实现了随机环境下多机器人系统的分布式自组织任务分配。文中深入探讨了智能体集合建立过程中的关键问题和博弈论中Nash稳定性分区建立的过程。最后对算法实现了仿真，仿真结果表明该决策框架具有良好的鲁棒性、可扩展性和良好的动态任务分配结果表现。对特定问题的模型构建和算法求解是解决精梳车间具体问题的关键，也是下一步在机器人本体应用调试的重要基础。在今后的研究中，将根据实际生产需求完善约束条件，进一步改进任务模型和决策框架，进行初步的多机器人多任务应用研究，使之适用更多的实际任务分配需求。