熔覆层厚度对相控阵表面波聚焦特性的影响

周永立，周 刚，胡宏伟，刘芝平

(长沙理工大学 汽车与机械工程学院，湖南 长沙 410114)

0 引言

激光熔覆是对零件进行表面改性、修复、增材制造等重要手段，在航空航天、海洋工程、汽车等重要工业中得到了广泛应用。然而熔覆过程中产生的应力及熔池流动性差，易导致裂纹、气孔和夹杂等缺陷[1]，严重降低了激光熔覆零件的使用性能，甚至会导致关键零件失效而引发重大事故，故对熔覆层进行检测极为重要。

超声无损检测具有检测速度快，灵敏度高及适应性强的优点，是常用的检测手段之一[2]，也是目前激光熔覆层检测的研究热点[3-4]。由于激光熔覆层厚度一般在3 mm以内，若采用超声纵波和横波对激光熔覆层表面缺陷进行检测，则难以避免出现熔覆层界面回波和缺陷回波重叠[5]，且纵波对表面缺陷的灵敏度较低。表面波可以有效避免上述问题，同时表面波能够探测到表面以下2个波长的深度，非常适用于厚度较薄的熔覆层的检测[6]。董世运等[7]建立了Fe314激光熔覆层中单探头表面波的声弹关系公式，且成功检测了激光熔覆层的应力。刘彬等[8]采用超声单探头表面波对激光熔覆层裂纹深度进行了评价，结果显示表层裂纹信号幅值随裂纹深度的增大而增大。受熔覆层各向异性组织及表面粗糙度等因素的影响，缺陷回波信号的信噪比低，使缺陷检测分辨率低[9]。与单探头超声表面波检测相比，超声相控阵表面波检测具有检测速度快，灵敏度高及能适应复杂对象的优势。Ohara等[6,10]和Xiang等[11]分别采用楔块式相控阵表面波和电磁超声相控阵表面波对表面缺陷进行检测，结果表明相控阵表面波对缺陷有较高的灵敏度。这些研究表明采用相控阵表面波检测激光熔覆层缺陷是可行的，但相控阵表面波的成像效果与缺陷处表面波能量相关且易受厚度的影响[12]。但是，上述研究均未考虑到厚度对相控阵表面波缺陷检测的影响，且由于实际工业生产的激光熔覆层厚度的变化，为了研究激光熔覆层相控阵表面波成像，有必要研究激光熔覆层厚度对缺陷聚焦能量的影响。

本文开展了超声相控阵表面波检测激光熔覆层的研究，首先采用有限元法建立单探头与阵列式超声表面波的传播模型，随后结合相控阵表面波的延时法则，研究了相控阵表面波的聚焦和偏转特性，最后研究了激光熔覆层的厚度对超声相控阵表面波聚焦特性的影响。

1 相控阵表面波检测原理

超声相控阵由多个独立换能器阵元按一定形状和尺寸排列构成，每个阵元都有自己独立的发射和接收电路，并不受其他阵元的影响。通过在每个阵元施加特定的延时来改变超声波声束的方向，从而达到合成声束偏转、聚焦的效果。对于常用的楔块耦合式相控阵表面波，当楔块角度大于第二临界角时，入射纵波会经楔块发生波形转换后在检测对象表面产生表面波。

以一维线性相控阵(见图1)为例，相控阵主要参数有：阵元个数N，阵元宽度a，阵元间距d，阵元间隙g，阵元总长度2L。阵元中心距熔覆层的高度为H，超声波在楔块和熔覆层内的传播速度分别为c1、c2。激励阵元i，接收阵元j，入射角θ，折射角θs，Si(xi,yi,zi)、Sj(xj,yj,zj)分别为声束在工件上的入射点和声束从工件反射至j阵元的点，F(x,y,z)为缺陷位置。

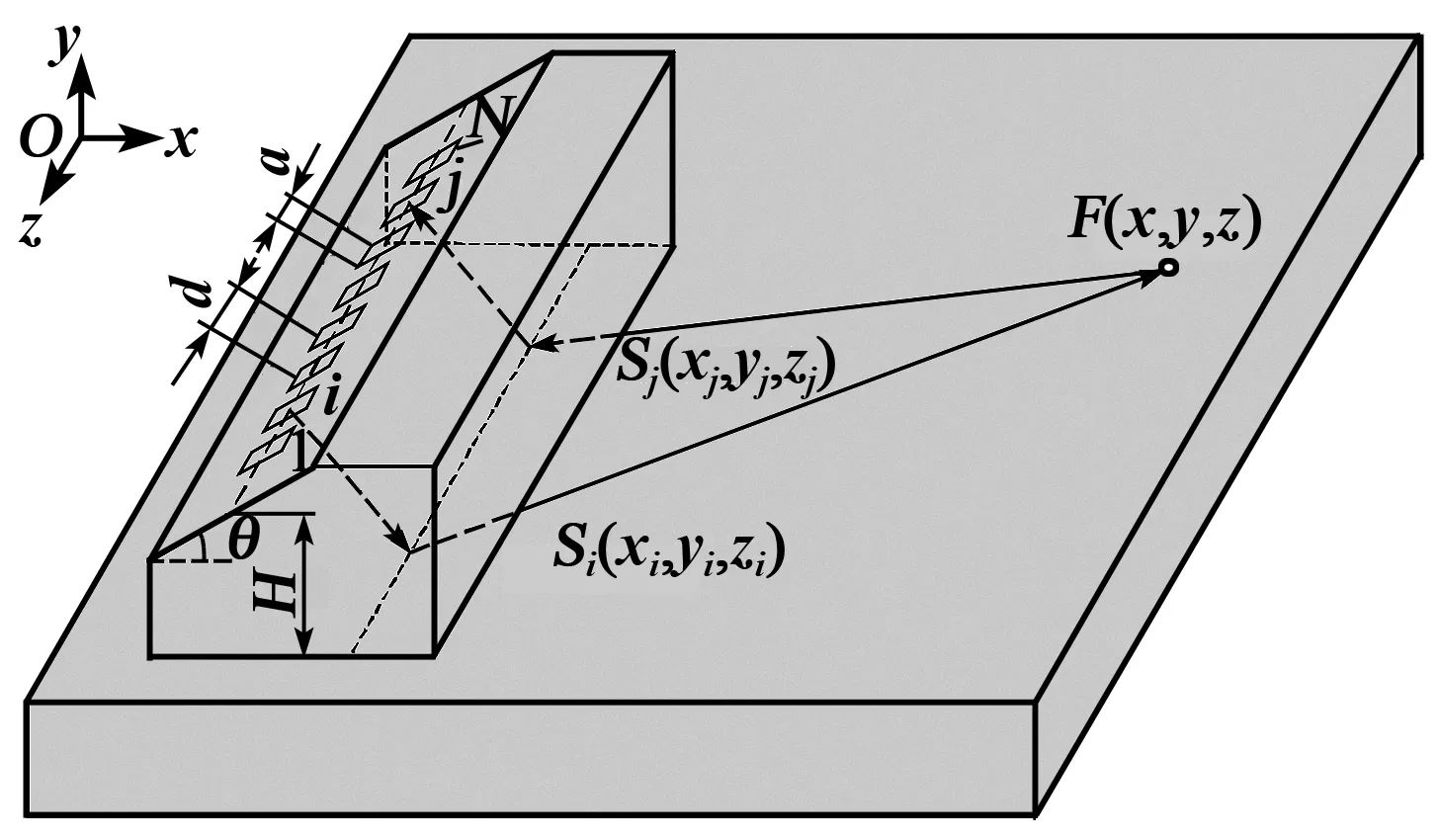
图1 相控阵表面波延时计算原理图

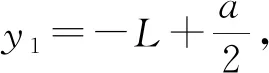
(1)

根据N、a和g可得L为

(2)

联立式(1)、(2)可得到第i个阵元的中心在y轴上的坐标yi为

(3)

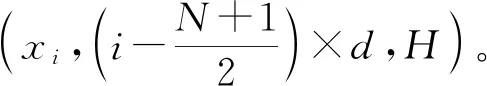
通过Snell定律：

(4)

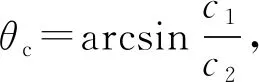
(5)

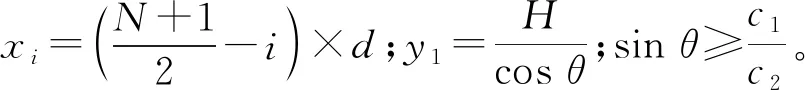
以其中最短传播时间min(Ti)的阵元为基础，从而可得到各个阵元上的时间延时Δti为

Δti=Ti-min(Ti)

(6)

通过设置各阵元上的Δti，可使声束聚焦到缺陷点F(x,y,z)处。

2 有限元仿真

2.1 表面波有限元理论

根据超声波的性质求解质点运动方程，可得表面波的振动位移在x，z方向的位移[13]分别为

u=a(k)sin[k(x-ct)]

(7)

w=b(k)cos[k(x-ct)]

(8)

式中：a(k)为与纵波分量有关的方程；b(k)为与横波分量有关的方程；c为超声传播声速；t为时间。

由能量守恒定律、动量守恒定律、介质状态方程及小振幅近似，再结合固体弹性介质中声场的线性方程[14]，可得到表面波在x，z方向声场的线性方程：

(9)

(10)

式中：ρ为密度；C为弹性系数；Fv为施加的外力。

本次仿真采用的是各向同性且均匀的材料，当引入拉梅常数λ，μ时，表面波在均匀各向同性弹性材料中传播的波动方程为

(11)

(12)

根据有限元计算标准步骤，首先将计算区域划分为若干单元和节点，然后构造唯一差值函数，并用节点唯一和位移插值函数表示四求解区域中任意一点位移，再根据伽辽金法并结合节点位移变分任意性，由式(11)、(12)导出系统的运动方程：

MA″(t)+CA′(t)+KA(t)=Q(t)

(13)

式中：A″(t)、A′(t)、A(t)′分别为系统的节点加速度向量、节点速度向量、节点位移向量；M、C、K、Q(t)分别为系统的质量矩阵、阻尼矩阵、刚度矩阵和节点载荷向量。

2.2 有限元仿真模型

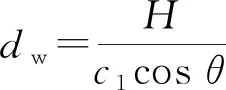
(0≤t≤3T0)

(14)

式中A=5×10-6m为振动幅值;T0为周期。

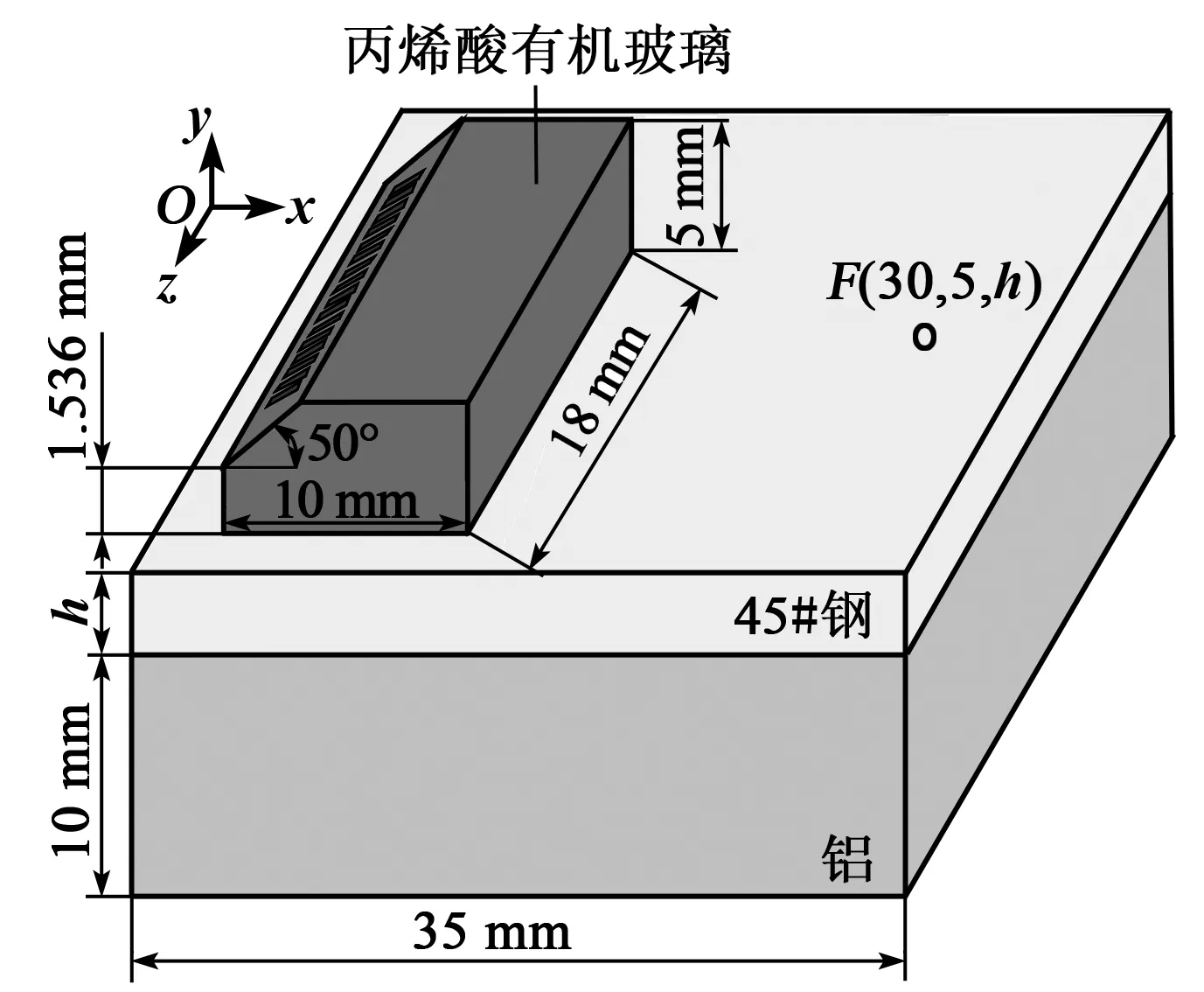
图2 三维仿真模型示意图

表1 各材料相关参数

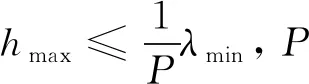
(15)

式中：fmax为超声波的最大频率;CFL=0.2。

经过计算可得到楔块中纵波的波长λw=2.077 mm，工件中表面波波长λs=2.951 mm，理论上，楔块与工件最大网格尺寸分别为0.415 4 mm和0.590 2 mm。其余厚度同上处理。

3 仿真结果与讨论

首先对常规的单探头检测进行仿真模拟，即将阵元数量设置为1个，仿真结果如图3所示。由图3(a)可知，在熔覆层表面传播时，超声波在z方向的运动轨迹是椭圆，说明采用特定角度的楔块能够在熔覆层表面产生表面波。从图3(b)、(c)可看出，表面波能量较小，缺陷处振动位移幅值为4.48×10-4mm。

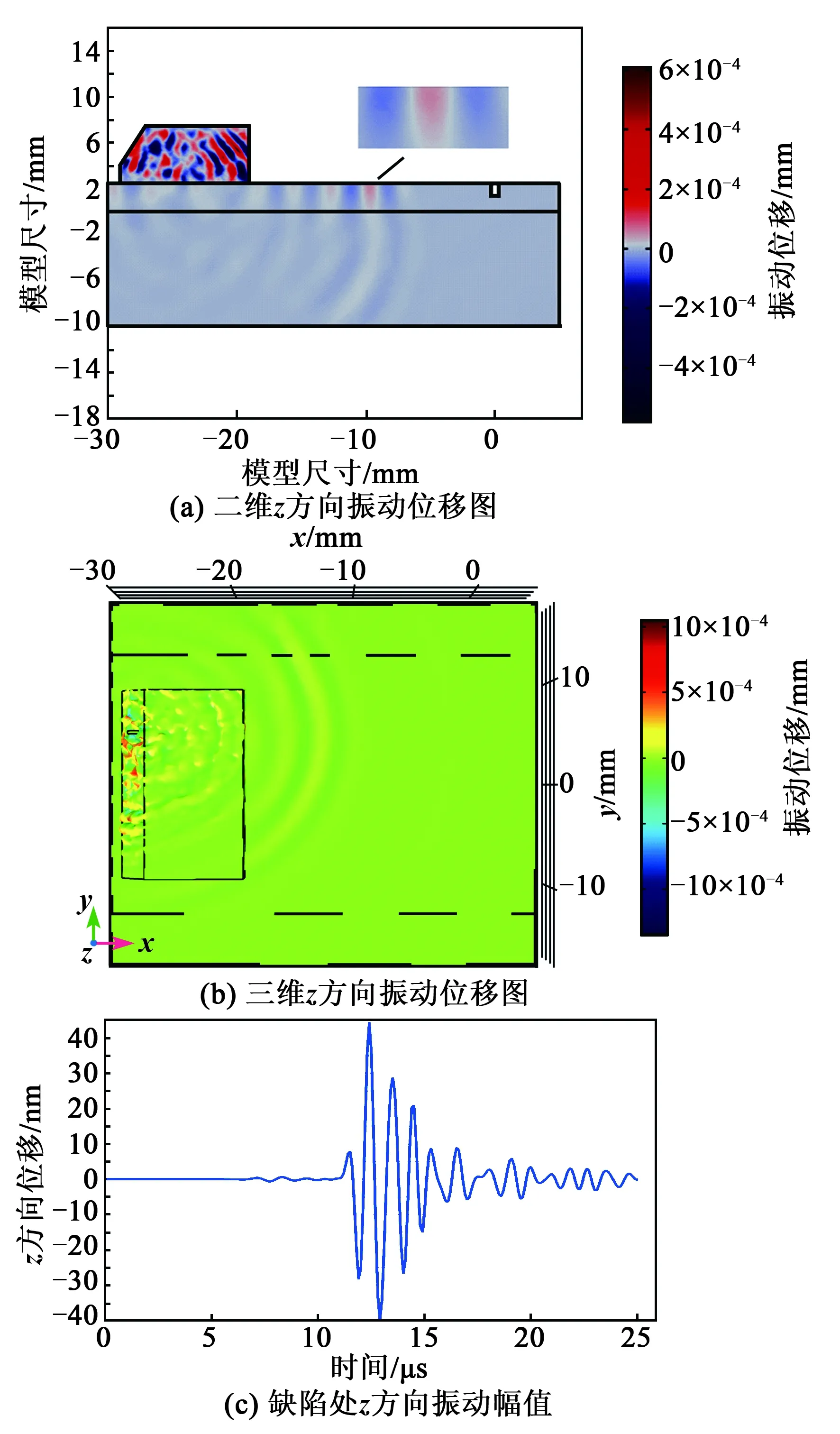
图3 单探头激励仿真结果

随后，对相控阵检测进行仿真模拟。根据相控阵表面波延时原理，由式(6)可计算出各个阵元1～N(图2中从下至上)施加如图4所示的时间延时，得到熔覆层厚度h为2.5 mm的仿真结果如图5所示。由图5(a)可知，无延时处理时，超声表面波声束沿着熔覆层表面扩散，最大振动幅值出现在中心处，其余位置的振动幅值较小，而由图5(b)可知，经过延时处理后，超声表面波声束明显聚焦在缺陷F(30,6,2.5)处，且聚焦能量相对于无延时处理的缺陷处能量有所提升，可提高工件任意成像点的分辨率。

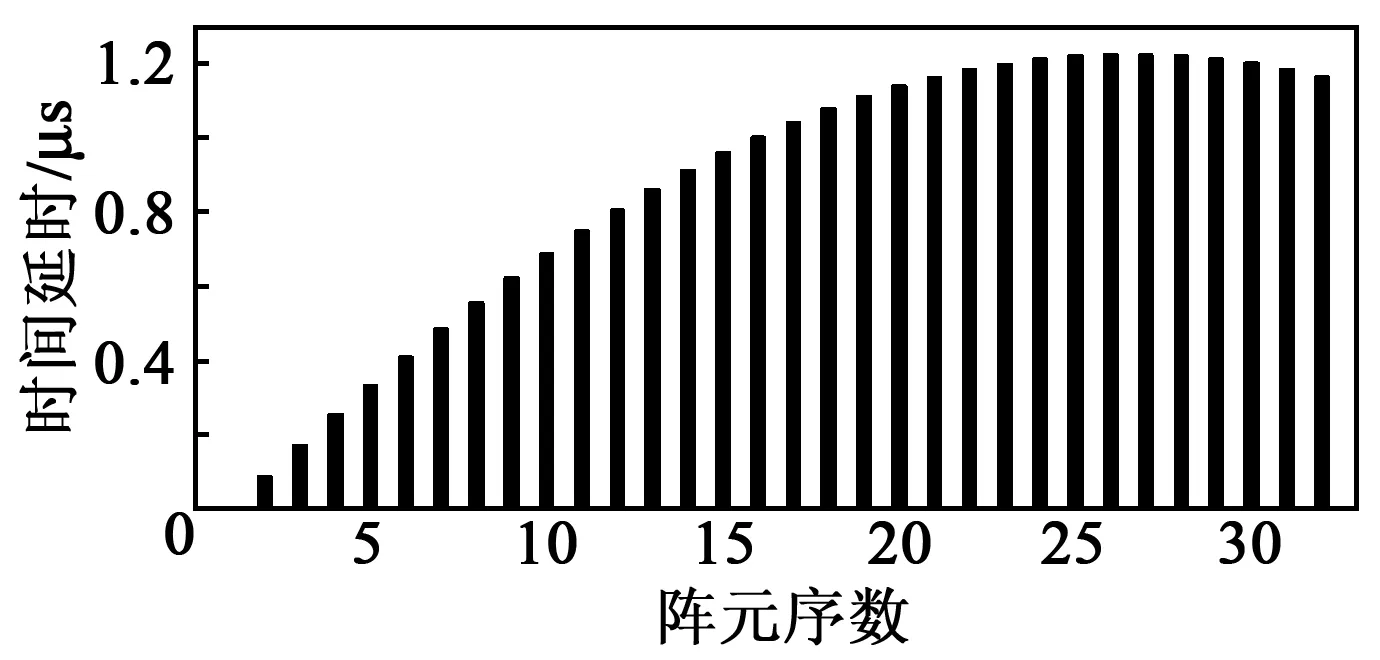
图4 各阵元上的时间延时图

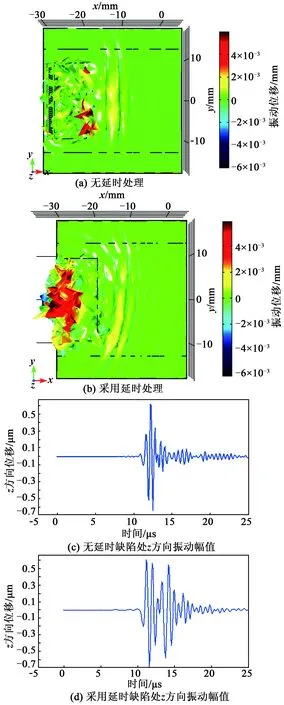
图5 相控阵激励仿真结果

与图3(b)相比，从图5(a)、(b)可看出,相控阵激励时，表面波能量明显大于单探头。对比图3(c)、图5(c)、(d)的振动幅值，计算可知相控阵表面波在缺陷处的振动幅值约为单探头的15.64倍。

考虑到表面波能探测2个波长(2λs=5.9 mm)深度内的缺陷，选取h=0.2 mm、0.3 mm、0.5 mm、0.6 mm、0.8 mm、1.0 mm、1.1 mm、1.3 mm、1.5 mm、1.6 mm、1.8 mm、2.0 mm、2.5 mm、…、5.0 mm，并在缺陷处采集到表面波最大振动位移如表2所示。

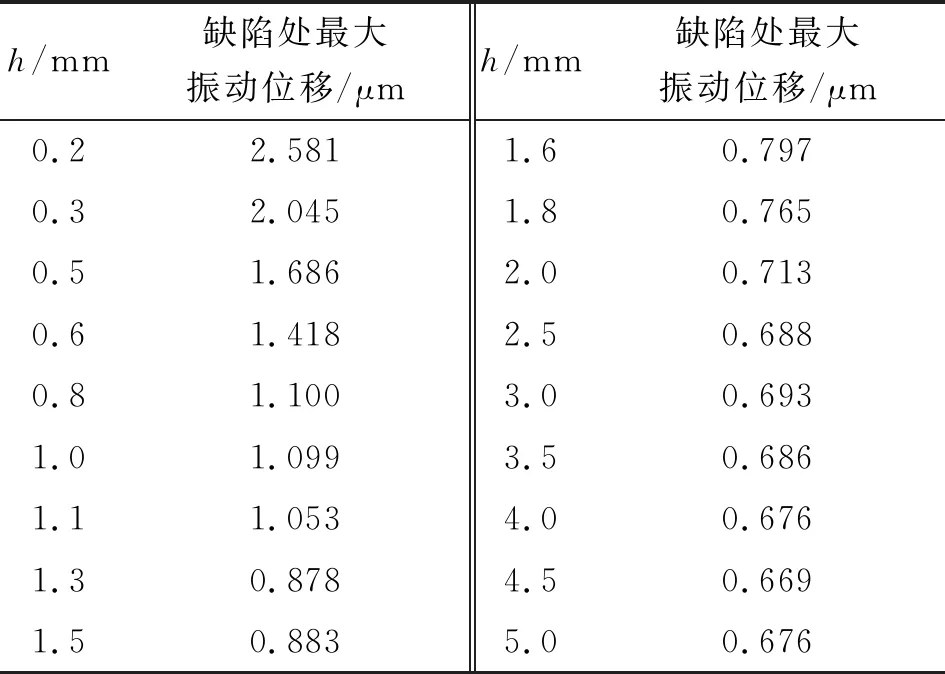
表2 熔覆层厚度对应缺陷处振动幅值

将上述结果进行拟合，得到h和缺陷处最大振动位移间的关系如图6所示。

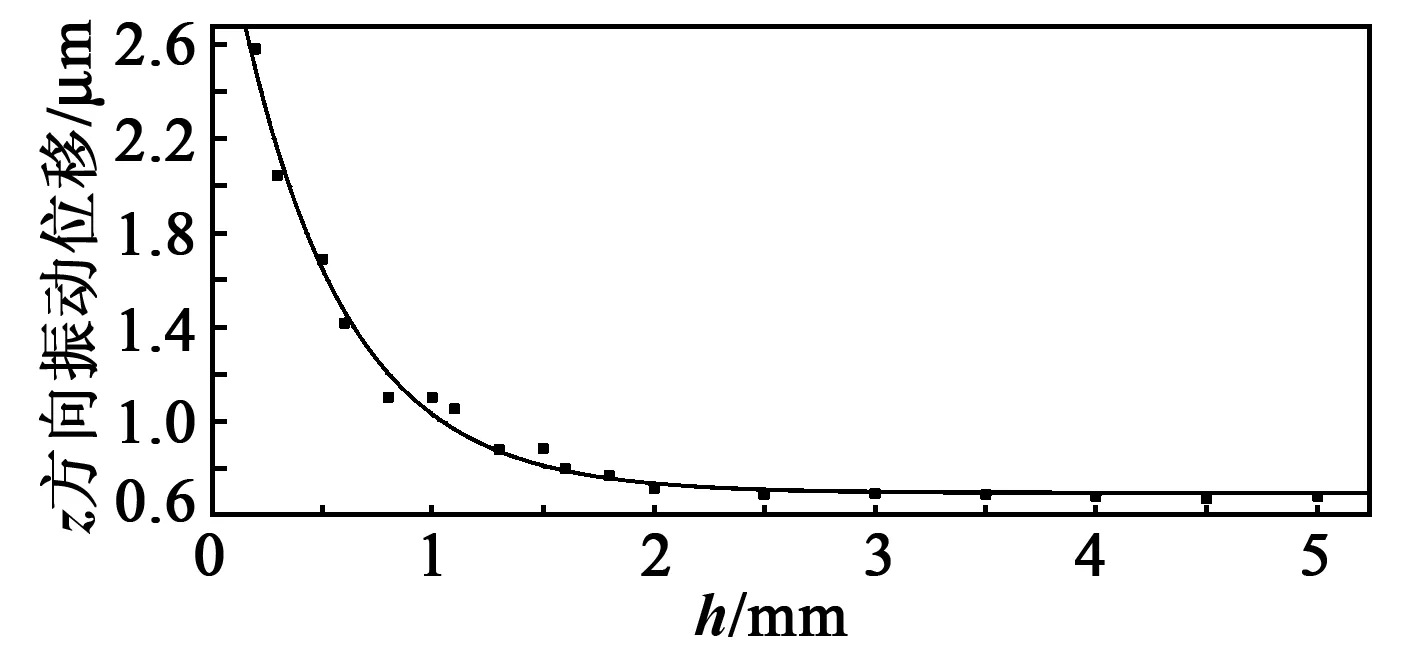
图6 h与缺陷处最大振动位移的关系

由图6可知，当h<1 mm时，随着h的增加，缺陷处表面波最大振动位移明显减小，当h=1～2 mm时，随着h的增加，缺陷处表面波最大振动位移缓慢减少，聚焦效果逐渐变差；当h>2 mm时，h越大，缺陷处表面波最大振动位移变化不明显，即在此距离区间聚焦效果变化不大。其中h增加到1 mm时，聚焦点处的能量(即最大振动位移)相对于h=0.2 mm时减小了58.8%，由此认为熔覆层越薄，相控阵表面波的聚焦特性越好。因此，相控阵表面波适用于薄的激光熔覆层的检测。

4 结束语

本文提出了采用相控阵超声表面波检测激光熔覆层缺陷的方法，建立了适用于相控阵表面波聚焦与偏转的延时算法。随后开展了相控阵表面波在熔覆层传播的有限元模拟，分析了熔覆层厚度对缺陷检测影响规律。结果表明,当熔覆层厚度小于1 mm时，随着厚度增大，聚焦点能量急剧减小；当厚度增加到1 mm时，缺陷处的能量相对于厚度为0.2 mm减小了58.8%；而当厚度达到2 mm时，聚焦点能量趋于稳定。仿真表明相控阵表面波对薄的熔覆层具有很好的检测效果。