静电场对压电薄膜中声表面波传播的影响
2021-01-05刘智荣谢立强包文歧
刘智荣,谢立强,朱 敏,包文歧
(陆军工程大学 国防工程学院, 江苏 南京 210007)
0 引言
声表面波(SAW)技术发展至今,在传感器和信号处理器上已得到了广泛的应用[1-3]。当外电场作用到SAW传播的压电介质上时,由于逆压电效应,会导致压电介质内部产生应力和形变,进而影响SAW的传播特性,因此,SAW可实现静电场的感测。用SAW实现静电场的感测,可有效解决现有电场传感器干扰抑制能力差,不能无失真感测的难题[4-5]。
要实现SAW对静电场的感测,首先必须探寻静电场与SAW传播之间的规律。Boris D. Zaitsev等[6]最早从压电材料弹性常数变化的角度,研究了外加电场对铌酸锂中瑞利波相速度的影响。Zhang R等[7]研究了具有初始应力的磁电弹性半空间中瑞利波的传播行为,得到了不同电、磁边界条件下波速的解析解。D. Koulova等[8]通过实验的方式研究了电场作用下绝缘液-空气界面上波的传播行为,分析了波长和角频率随电场变化的规律。
关于静电场对压电薄膜上SAW传播的影响机理,目前国内外的研究较少。为此,本文在静电场导致压电薄膜产生初应力和形变的基础上,利用小幅波动理论建立和求解了波动方程,并通过仿真分析讨论了两种压电薄膜材料SAW在静电场影响下的相速度变化和频散曲线。
1 波动方程的建立
1.1 初始条件
图1为一静置于静电场(E)中的无限大横观各向同性压电薄膜,其厚为h,极化方向沿着z轴,坐标平面xOy与压电薄膜的中面重合。E方向沿着压电薄膜的极化方向。
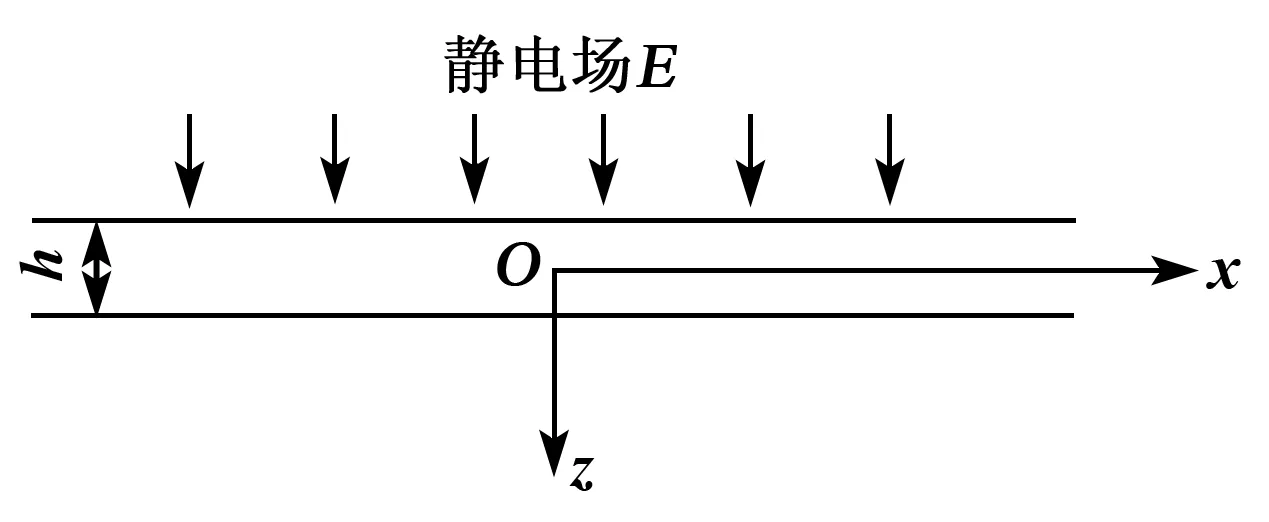
图1 静电场中的压电薄膜
根据假设条件,可由压电本构方程得到静电场作用下压电薄膜中的初始应力和初始电位移为
(1)
式中:c13、c33为压电薄膜的弹性常数;e31、e33为压电系数;ε33为介电常数。
1.2 波动方程
研究了静电场对压电薄膜SAW传播行为的影响,即在波动分析中考虑静电场作用下的初始应力和初始电位移。具有初始应力和初始电位移的压电介质小幅波动问题的运动方程[9-11]为
(2)
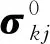
若SAW沿x方向传播,则压电薄膜中质点的机械位移u=u(x,z,t)、v=0、w=w(x,z,t)和电势函数φ=φ(x,z,t)。于是式(2)可化简为
(3)
由于波传播与y方向无关,因此,压电薄膜的本构方程为
(4)
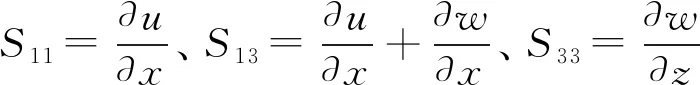
将式(1)、(4)代入式(3)中,得到由机械位移分量及电势函数表示的波动微分方程:
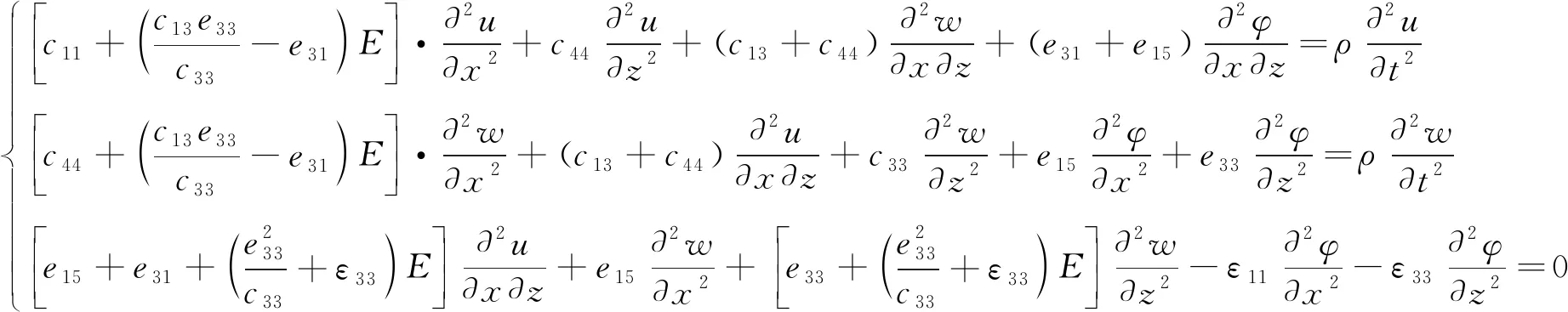
(5)
2 波动方程的建立
设压电薄膜中质点的u、w和φ的解分别为
(6)
式中:c为SAW相速度;k=2π/λ为波数,λ为SAW波长;a为待定系数;A1、A2、A3分别为u、w、φ的幅值。
1.4 观察指标 比较两组患者治疗后的临床有效率,以及治疗前后裸眼视力、血糖相关指标(空腹血糖、餐后2 h血糖、糖化血红蛋白)、血液流变学相关指标(血浆黏度、红细胞聚集指数、红细胞变形指数)、血清相关因子(血管内皮生长因子、低氧诱导因子-1α)等水平变化。
将式(6)代入式(5)中,有
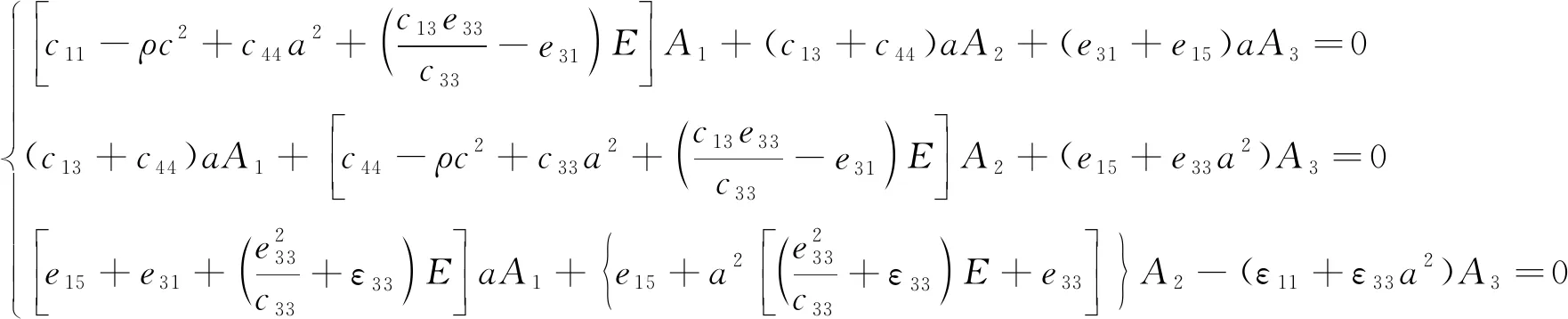
(7)
要使式(7)有非平凡解,须使其系数行列式等于0,且该行列式可看成是以c及E为参数、a为未知量的1个6阶代数方程。由于z→时,SAW的位移衰减至0,因此,a仅取虚部为正的3个根,记为an(n=1,2,3)。式(7)可表示为
(8)
其中
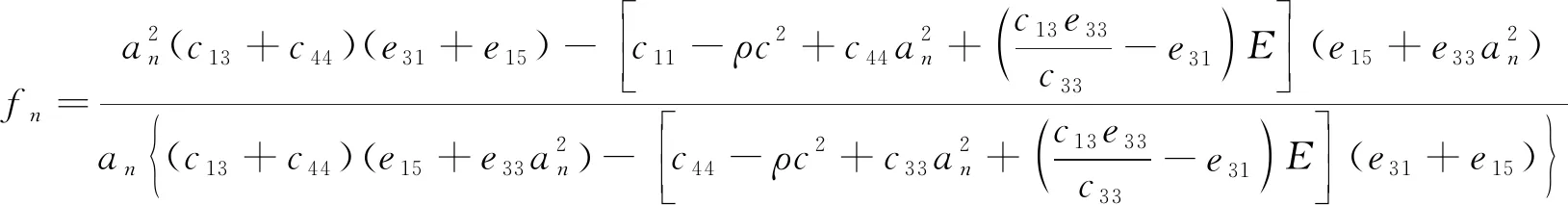
(9)
(10)
压电薄膜的上、下表面外力自由,且可视为电学短路,因此,边界条件有
(11)
故压电薄膜的位移和电势函数的完整解应为
(12)
(13)
其中Q为3阶方阵,其元素Qpn(p=1,2,3;n=1,2,3)为
Q1n=(c13+c33fnan+e33gnan)e±ikanh/2
(14)
Q2n=(c44an+c44fn+e15gn)e±ikanh/2
(15)
Q3n=gne±ikanh/2
(16)
为使A有非平凡解,则有
|Q|=0
(17)
式(17)即为SAW的相速度或频散方程。
3 仿真分析及讨论
本文选用氧化锌(ZnO)和氮化铝(AlN)这两种压电薄膜材料,分析其SAW传播特性。这两种材料的性能参数如表1所示。

表1 压电材料相关参数
设定E=0~10 kV/mm。设m=h/λ为压电薄膜厚度与SAW波长之比(厚波比),当m=1、2、5、10时,通过仿真可得c与E关系如图2所示。由图可知,无论m取何值,两种材料中的c都随E的增加而线性增加,其中ZnO和AlN相速度曲线斜率
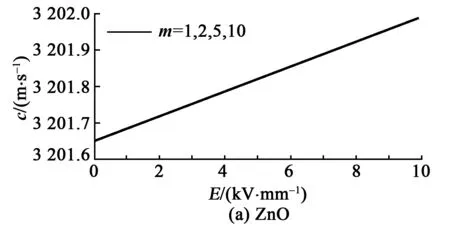
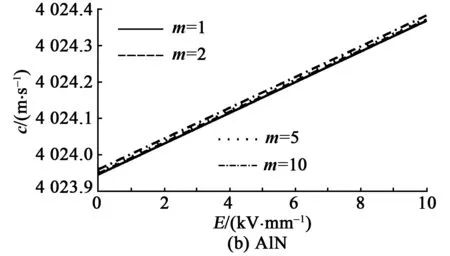
图2 ZnO、AlN材料中c与E的关系
分别为0.106和0.117,可见ZnO和AlN材料中SAW对E的敏感度相当。尽管m取值不同,但曲线几乎重叠,符合c与压电薄膜材料的物理尺寸无关,但与弹性性质、压电性质及介电特性有关的研究理论[12]。
图3为在不同E的作用下,h=0.1 mm时ZnO和AlN所对应的频散曲线。由图可知,在E的作用下,SAW传播的c在波数较低(k<2×105/m)时变化明显,由λ=2π/k可得,即当λ>31.4 μm时,SAW对E的变化更敏感。在k→,即波频率f=kc/2π非常高时,c逐渐平稳并趋向于剪切体波波速,此时E对c的影响较小。此外还可发现,在同一波数下,E越大,对应的c越小。
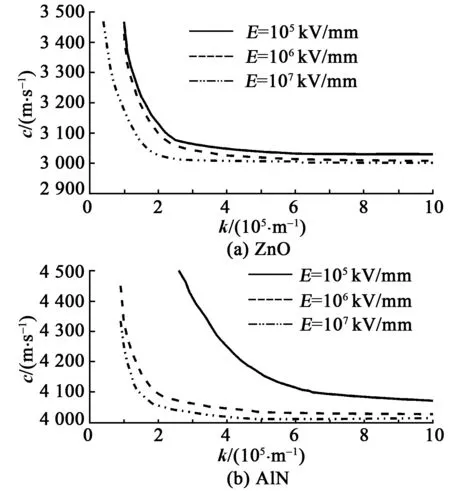
图3 静电场作用下ZnO、AlN材料的频散曲线
这一物理现象本质是静电场作用下,由于逆压电效应,压电薄膜内部产生了应力场和电位移场,使SAW的传播行为受到影响。综上可知,只需要测量出c的实际值,便可得出对应静电场值,这可以作为测量静电场大小的一种方法。
4 结束语
本文得到了静电场作用下声表面波在压电薄膜中传播的相速度变化及频散曲线。在压电薄膜材料参数给定的情况下,静电场值越大,声表面波的相速度越大。波数越小,声表面波对静电场的变化越敏感;波数越大,即频率越高时,声表面波的相速度越小。因此,通过对声表面波相速度的测量可以确定外加静电场值的大小。
