还原直观图 巧解几何题*
2020-12-28张全合
张全合
(北京市昌平区第一中学,102200)
在立体几何解题中,有时会遇到题中未给出几何体的直观图,而是给出与题设的几何体密切相关的一些图形;或者试题只用语言叙述,根本不给出具体图形.这类题型考查学生的空间想象力,解题时只要根据题意还原几何体的直观图,即可加强问题的几何直观,有利于寻找解题方法,甚至是巧招妙法.
一、由三视图还原几何体的直观图
例1(2020年全国高考题)如图1,是一个多面体的三视图,这个多面体某条棱的一个端点在正视图中对应的点为M,在俯视图中对应的点为N,则该端点在侧视图中对应的点为( )
(A)E(B)F(C)G(D)H
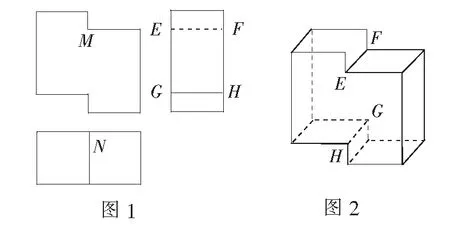
解由三视图还原多面体的直观图如图2,即可判断出所求对应的点为E.选A.
二、由截面图还原几何体的直观图
例2(2006年湖南高考题)棱长为2的正四面体的四个顶点都在同一球面上,若过球心的一个截面如图3,则图3中的三角形(正四面体的截面)的面积是( )
分析由图3可知,过球心的截面三角形是等腰三角形,该等腰三角形的底边是截面圆的弦,它必是球面内接正四面体的一条棱;该等腰三角形的顶点必是这条棱所对的棱的中点.
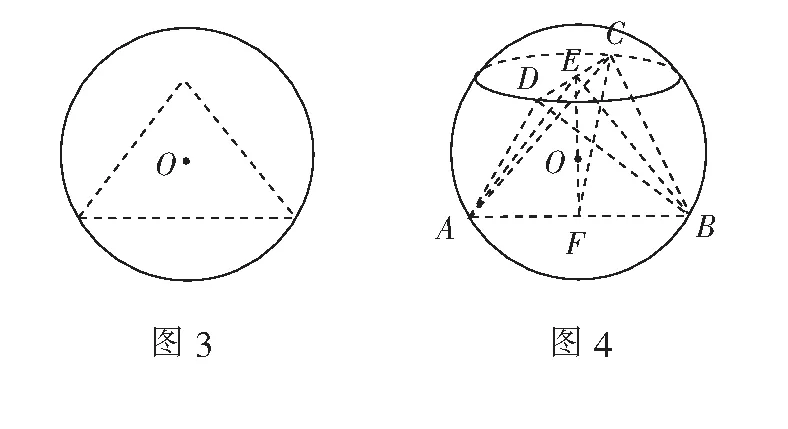
解还原球面O的内接正四面体ABCD,如图4,记E为棱CD的中点,则图3中的截面是∆ABE.
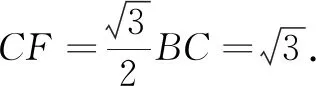
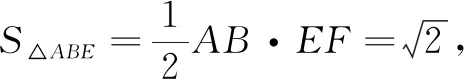
三、由侧面展开图还原几何体的直观图
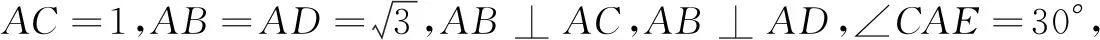
分析图5中点D,E,F即为原三棱锥的顶点P,还原三棱锥P-ABC,如图6.所求即为三棱锥中的cos∠PCB,只要求∆PCB的三边长.

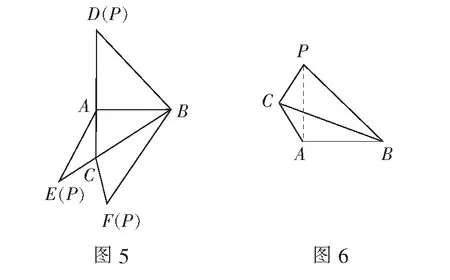
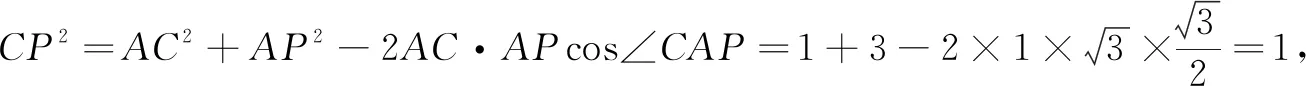
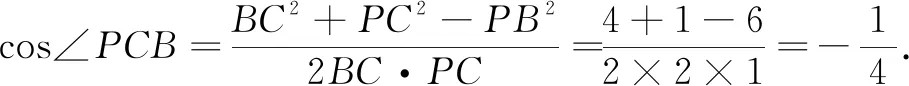
四、由局部图形还原几何体的直观图
例4(2009年江西高考题)如图7,正四面体ABCD的顶点A,B,C分别在两两垂直的三条射线Ox,Oy,Oz上,则在下列命题中,错误的为( )
(A)O-ABC是正三棱锥
(B)直线OB∥平面ACD
(C)直线AD与OB所成的角是45°
(D)二面角D-OB-A为45°
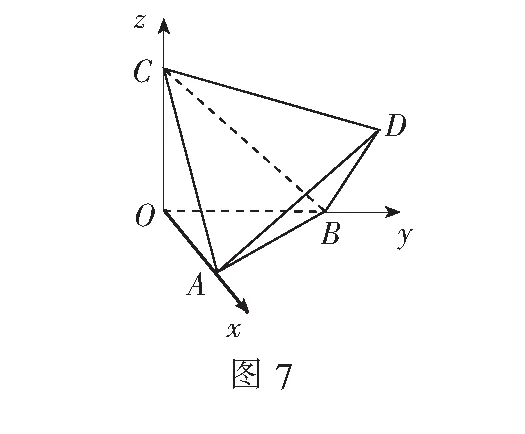
分析由图7中的正四面体的棱长相等及射线Ox,Oy,Oz两两垂直的条件,可构造正方体OAQB-CEDF如图8,则正四面体ABCD的各棱是这个正方体的面对角线.
解法1如图8,因OA2+OB2=OB2+OC2=OC2+OA2,有OA=OB=OC,故O-ABC是正三棱锥,A真;因直线AD与OB所成的角为∠DAQ=45°,C真;因二面角D-OB-A的平面角为∠DBQ=45°,D真.排除ACD,所以选B.
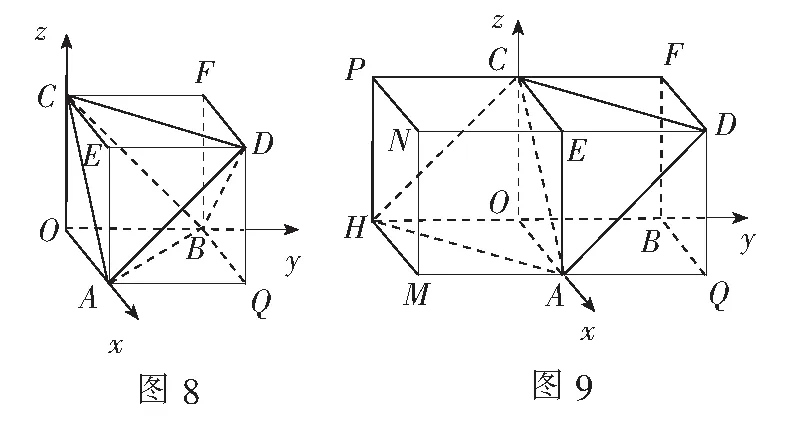
解法2如图9,在正方体OAQB-CEDF的左边再构造一个全等的正方体HMAO-PNEC,则MQBH-NDFP是长正方体,平面ACD即平面ADCH.直线OB与平面ADCH相交于点H,这说明直线OB与平面ACD相交于点H.所以选B.
例5(2005年全国高考题)如图10,在多面体ABCDEF中,已知ABCD是边长为1的正方形,且∆ADE,∆BCF均为正三角形,EF∥AB,EF=2,则多面体的体积为( )
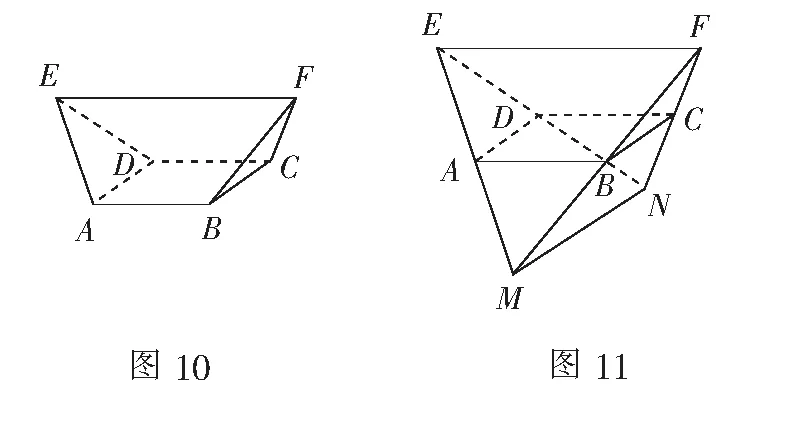
分析若再有一个与之全等的多面体,将这个全等的多面体倒置且旋转90°后与原多面体对接,可得一个棱长为2的正四面体,这个正四面体体积的一半即为所求.
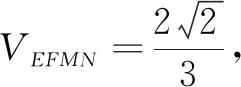
评注此题解法较多,上述解法可谓巧招妙法.
五、由解析式的特征构造几何体的直观图
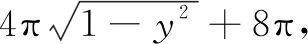

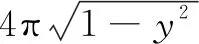
解过点(0,y)(|y|≤1)作Ω的水平截面,截平放的圆柱O-O1和长方体ABCD-A1B1C1D1,分别得如图13的矩形EFMN和如图14的矩形PQGH.
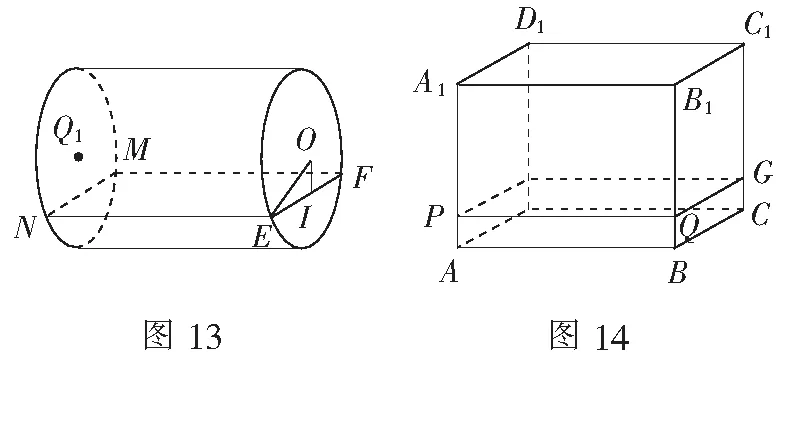
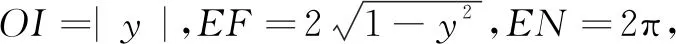
在图14中,AA1=2,BC=2,AB=4π,SPQGH=SABCD=8π.
因为过点(0,y)(|y|≤1)作Ω的每一个水平截面的面积等于该截面截平放的圆柱O-O1和长方体ABCD-A1B1C1D1所得两个截面的面积之和,由祖暅原理知Ω的体积VΩ=V圆柱+VABCD-A1B1C1D1=π×12×2π+8π×2=2π2+16π.
六、由文字叙述画出几何体的直观图
例7(2020年全国高考题)如图15,日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针到晷面的影子来测定时间.把地球看成一个球(球心记为O),地球上一点A的纬度是指OA与地球赤道所在平面所成的角,点A处的水平面是指过点A且与OA垂直的平面.在点A处放置一个日晷,若晷面与赤道所在平面平行,点A处的纬度为北纬40°,则晷针与点A处的水平面所成的角为( )
(A)20° (B)40° (C)50° (D)90°
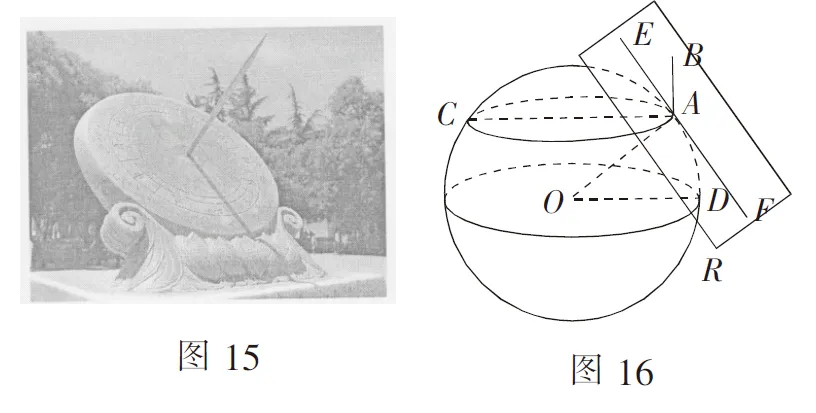
分析画好说明该问题的直观图如图16.用AB表示晷针,设点A处的水平面是α,平面α与过OA且与赤道所在平面垂直的平面相交于直线EF.由题意知EF是大圆O的切线,∠AOD=40°,∠BAE为所求.由∠BAE的两边与∠AOD的两边两两垂直,知∠BAE=40°.
解如图15,因为∠OAC=∠AOD=40°,OA⊥EF,AB⊥OD,所以∠CAE=50°,晷针与点A处的水平面所成的角∠BAE=40°.选B.
还原几何体的直观图,使我们清晰地认识了问题的庐山真面目,助力了解题思路的产生与发展.这需要我们对于基本的几何体及其直观图很了解,并且具有足够的想象力.在还原几何体的直观图解题的过程中,我们品味了数学之美,寓解题于快乐之中,趣味横生.
