可重构智能表面通信系统的渐进信道估计方法

党 建, 李业伟, 朱永东, 郭荣斌, 张在琛,*, 吴 亮

(1. 东南大学信息科学与工程学院, 江苏 南京 210096; 2. 网络通信与安全紫金山实验室, 江苏 南京 211111; 3. 之江实验室, 浙江 杭州 311121)

0 引 言

近年来,随着无线通信技术的快速发展,以可重构智能表面(reconfigurable intelligent surface,RIS)为代表的人工电磁材料作为极具前途的辅助技术被引入无线通信系统中。RIS是由大量无源反射单元所组成的平面阵列,从微观上看,可以人为地控制每个反射单元的反射系数(包括相位和幅度),使其对入射的电磁波独立施加可控影响;从宏观上看,可以协同控制所有反射单元,来改变反射波束的数量、方向、散射程度等。因此,RIS能够实现对无线通信系统传播环境的改造,使得收发机之间的等效传输信道在一定程度上可控,从而提高通信系统的性能,实现信号的优化传输。

当RIS被部署在无线通信系统中时,需要设计合适的反射系数,才能获取到最佳的性能增益。RIS最优反射系数的计算与信道状态信息(channel state information, CSI)相关,因而一般是在完成信道估计后才配置最优反射系数。然而,对RIS进行信道估计面临比传统信道估计更大的挑战:RIS在进行信号反射时,其功能上属于被动无源器件,不具备信号接收、采样功能,仅能从收发端进行低维信号采样,并据此估计高维CSI。当RIS的反射单元数目较多时,待估计信道矩阵的维度较大,信道估计所需开销和计算复杂度很高。

近来,已有多种和RIS信道估计相关的技术路线被提出,比较有代表性的技术路线包括:① 从硬件功能着手,改变RIS的被动反射特性。文献[8-9]中从硬件结构方面对RIS做了改进,即RIS中除了包含被动反射单元外,还包含由射频链路控制的主动反射单元。这些反射单元可以对到达信号进行接收采样,因此RIS端可以独立完成信道估计过程。该方案的主要缺陷是增加了RIS的硬件成本,且并未从根本上减小待估计矩阵的维度。② 针对反射系数配置依赖于级联信道的事实,对级联信道进行估计,从而减小待估计参数个数。文献[10]研究了RIS辅助的大规模多输入多输出(multiple input multiple output,MIMO)系统的信道特性,提出了一种三阶段的信道估计协议,并指出大规模MIMO能够帮助减小待估计参数的数目,但其下界仍然不小于反射单元数目。文献[11]指出在设计不同导频对应的反射系数时,反射系数矩阵应该满秩,因而一般采用随机反射系数的配置方法。该文献进一步提出了一种特定反射系数配置方法使得信道估计的均方误差最小化,但在估计过程中所使用的导频数目仍然大于反射单元数目。③针对毫米波频段波束域信道模型,采用稀疏信号检测技术来估计波束角度和增益参数。文献[12-13]均提出了基于压缩感知的信道估计方法,先后求解出信道中的角度和路径增益。然而该类方法只适用于稀疏性信道模型,不适用于低频频段等非稀疏信道的通信场景,且其中求解稀疏问题时涉及到克罗内克积运算,需要极大的计算量来获得精确的估计值。

综上所述,现有的RIS信道估计方法仍然普遍存在导频开销大等问题,造成大量时间用于发送导频和信道估计而使得系统频谱效率下降。其根本原因在于当RIS的反射系数处于随机配置状态时,接收端功率较小、信噪比(signal-to-noise ratio, SNR)较低且不稳定,无法尽早开始发送数据。如果能在信道估计过程中令RIS配置特定的优选反射系数,即可稳定和逐步增大接收信号功率,进而使得接收端能实时监测信号功率,并通知发射端尽早开始数据传输,减小导频开销。

基于以上分析,本文提出一种将信道估计过程与反射系数配置相结合的传输方法。该方法的核心思想是在初始时刻为RIS配置随机反射系数,发射端发送导频,接收端通过松弛最小均方误差(relaxed minimum mean square error, RMMSE)方法来估计出级联信道,并利用估计所得的非完整信道状态信息来计算下一时刻的最优反射系数,并对RIS配置由最优反射系数和随机反射系数组成的混合反射系数。接下来重复信道估计与混合反射系数配置的步骤。随着发送导频数目的增加,信道估计的结果越来越接近于真实信道,计算所得的最优反射系数也越来越接近于完整信道状态信息下的最优反射系数,接收信号功率也会稳定、渐进增加,接收端可持续监测信噪比是否达到预定门限,若达到则通知发射端尽早开始数据传输,减小导频开销。

1 系统模型

本文考虑上行链路的单输入多输出(single input multiple output,SIMO)系统模型,RIS被部署来辅助一个单天线用户到基站的数据传输,如图1所示。

图1 一个RIS辅助的上行通信系统Fig.1 A RIS-assisted uplink communication system

基站为均匀线性阵列(uniform linear array,ULA),配置根天线。RIS为均匀方形阵列(uniform planar array,UPA),配置个反射单元,其反射系数由基站控制。∈×1表示用户到基站的直达信道,∈×1表示用户到RIS的信道,∈×表示RIS到基站的信道。在第个时刻,基站接收到的上行信号为

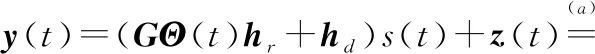
(1)

本文采用与文献[14]类似的信道模型,具体如下。由于用户和基站之间的视距(line of sight,LoS)信道可能会被遮挡,因此被建模为瑞利衰落信道,其每个元素都是独立同分布的零均值单位方差复高斯随机变量。在实际部署中,为了保证通信系统的性能,RIS与用户和基站之间均存在LoS链路,因此用户和RIS之间的信道被建模为莱斯衰落信道:

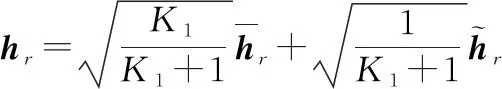
(2)

(,)=()⊗()

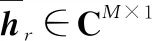
(3)

式中:⊗表示克罗内克积;和分别表示用户发射的信号在RIS的水平方向和竖直方向上的到达角(angle of arrival,AoA)。令=2π(cos),=2π(sincos),表示RIS的反射单元间距,表示信号载波波长,则

{()=[1,ej,ej2,…,ej(-1)]

()=[1,ej,ej2,…,ej(-1)]

(4)

类似地,RIS和基站之间的信道也被建模为莱斯衰落信道:

(5)

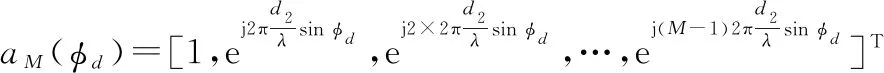
(6)

式中：表示基站处信号AoA；和分别表示信号经RIS反射后在水平方向和竖直方向上的离开角(angle of departure,AoD)；表示基站处天线间距。

2 信道估计方法

2.1 方法流程介绍

由于用户与基站之间的直达信道可以在关闭RIS的状态下利用传统信道估计方法快速获得,因此本文提出的估计方法中只对RIS信道进行估计,该方法的帧结构与反射系数配置流程图如图2所示。

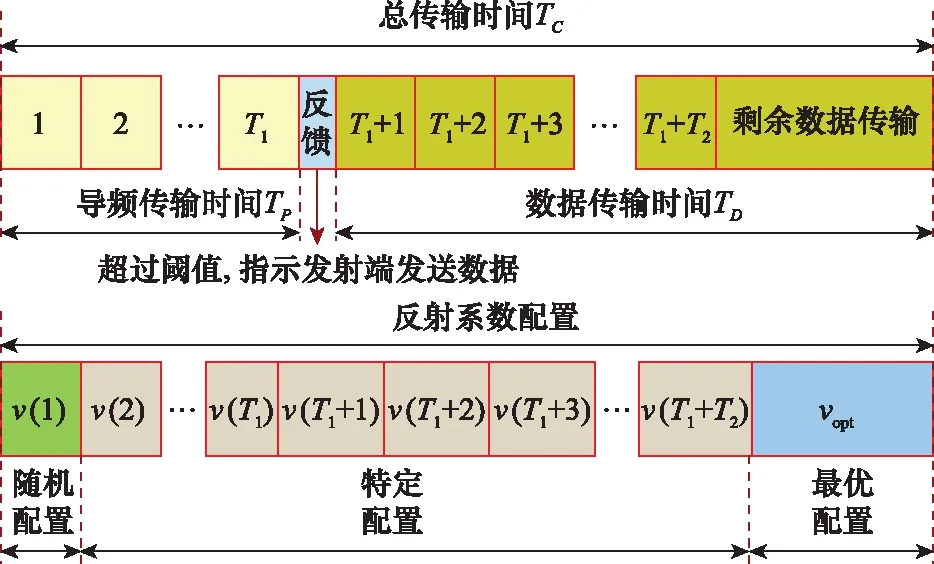
图2 信道估计方法的帧结构与反射系数配置流程图Fig.2 Flow chart of the frame structure and reflection coefficients configuration of the proposed channel estimation method

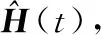
2.2 级联信道估计

在本文的通信模型中,用户为单天线,且用户与基站之间除了有级联信道矩阵外,还存在RIS的反射系数矢量。记时刻用户发送的导频标量符号为(),可以将时刻RIS的反射系数矢量()与导频符号的乘积重定义为“导频向量”,即()=()()。设用户总共发送了个导频符号,则由不同时刻的“导频向量”所组成的“导频信号矩阵”为

=[(1),(2),…,()]∈×

(7)

根据计算可知,级联信道相关矩阵的迹为

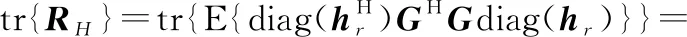
(8)

令=[(1),(2),…,()]∈×为基站处经RIS反射信号的接收矩阵,表示噪声方差,可得RIS级联信道的RMMSE估计公式为

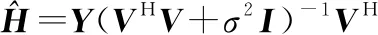
(9)

从式(9)可以看出,即使莱斯衰落因子及视距分量等先验信道信息未知,信道估计仍可正常进行。然而,本文中对级联信道的估计并非一次性完成,而是一个与反射系数配置结合的渐进估计的过程。当RIS配置新的反射系数之后,基站获得新的接收信号,则矩阵和都要新增加一列,并通过计算获得新的信道估计值,再利用该估计值去计算下一时刻的最优反射系数。在该过程中,式(9)涉及到矩阵的求逆问题,随着发送导频数目的增加,待求逆矩阵的维度也在不断增大。为了减小计算复杂度,本文采用如下分块矩阵求逆公式来避免多次求逆运算。

设为×的可逆矩阵,是×矩阵,是×矩阵,是×矩阵,=-是×的可逆矩阵,则

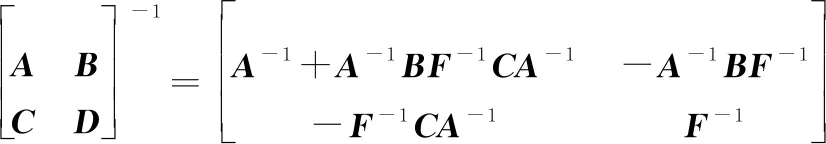
(10)

(11)

3 反射系数配置

3.1 最优反射系数的求解

获取估计信道值之后,根据式(1),为了使接收信号功率最大化,求解最优反射系数的问题可以等效为

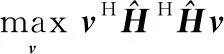
(12)

式(12)可以采用半正定松弛(semidefinite relaxation,SDR)的方法来解决,但求解过程中涉及到凸优化、矩阵分解等问题,其计算量较大,适用于在信道估计完成后一次性求解最优反射系数的场景,而不适用于在信道估计过程中多次求解最优反射系数的场景。

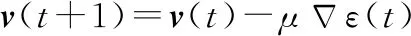
(13)

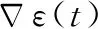
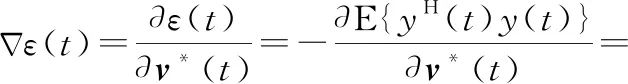
(14)

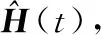
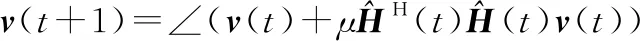
(15)

式中：∠代表将每个反射单元的反射系数的幅度值进行归一化,即只取其相位值。需要指出的是,虽然在渐进估计过程中,仍然将按照式(15)得到的反射系数称为最优反射系数,但因为其是基于部分导频得到的,因而是局部最优而不是全局最优的,这里是为了与随机配置反射系数进行区分。

一般情况下,反射单元个数大于基站天线数,且级联信道矩阵的秩为rank()=。在使用式(15)求解出+1时刻的局部最优反射系数后,若对RIS配置该反射系数,则会导致估计出的级联信道矩阵结果秩亏。

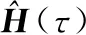
(16)

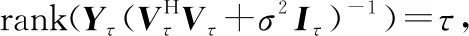
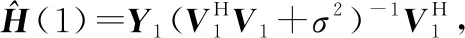
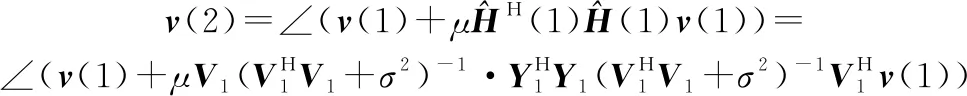
(17)

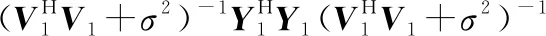
证毕

3.2 混合反射系数配置

依据第31节的分析,若在信道估计过程中给RIS配置局部最优反射系数,会使信道估计结果准确度降低,而配置随机反射系数时,接收信号功率较小,接收端信噪比较低。为了解决该问题,本文在局部最优反射系数配置方法的基础上进行改进,提出一种混合型反射系数配置方法。

设根据式(15)计算出的+1时刻局部最优反射系数为(+1),则下一时刻RIS配置的反射系数为局部最优反射系数与随机反射系数加权而成的混合反射系数,其表达式为

(+1)=∠(ω(+1)+(1-)(+1))

(18)

式中:(+1)表示+1时刻的任意随机反射系数；(0<<1)表示局部最优反射系数的归一化权重,1-表示随机反射系数的归一化权重。由于式(18)的反射系数中包含随机反射系数,故能够保证信道估计结果不秩亏,同时其又包含局部最优反射系数,可以让接收端的功率逐步增大。

综上所述,本文提出的信道估计算法步骤如下。

算法 1 RIS级联信道的估计算法初始化:RIS配置随机反射系数,归一化误差门限ε,数据传输信噪比门限ρ,T代表信道估计结果趋于稳定的时刻,发射端开始发送导频符号1. for t=1:T2. 获取估计信道:^H(t)=Yt(VHtVt+σ2It)-1VHt3. 计算下一时刻局部最优反射系数: vo(t+1)=∠(v(t)+μ^HH(t)^H(t)v(t))4. 判断估计信道是否趋于稳定:if E[^H(t-1)-^H(t)2F^H(t)2F]<ε then5. RIS配置反射系数vo(t+1)6. 信道估计完成:break 7. else8. 计算下一时刻混合反射系数:vm(t+1)=∠(ωvo(t+1)+(1-ω)vr(t+1))9. 判断接收端信噪比是否达到门限:if SNR(t)>ρ&&SNR(t-1)<ρ then

10. 接收端通知发射端开始发送数据11. end if12. 继续信道估计:RIS配置反射系数vm(t+1)13. end if14. end for

4 仿真与数值结果分析

本节采用数值仿真的方法来评估提出的信道估计算法给RIS辅助通信系统所带来的性能提升。在仿真场景中,基站端配置=16根天线,天线间距设置为半波长。RIS含有=16×16个反射单元,反射单元间距设置为半波长。信道模型中,视距分量的角度参数,,均从[0,2π)的范围内独立随机生成,信道莱斯因子设置为==132 dB。用户发送的导频信号为服从均值为0,方差为1的复高斯分布的随机数,修正公式中的正值步长设置为=1。根据文献[10]中的结论,传统信道估计方法至少需要个时隙来获取信道估计结果,因此仿真中涉及的总时隙数设置为==256。

4.1 估计信道矩阵的秩

为了验证第3.1节中的配置局部最优反射系数会导致估计信道秩亏这一结论,仿真中分别在有噪声和无噪声的场景下对RIS配置局部最优反射系数来进行信道估计,并将其与有噪声场景下RIS配置随机反射系数的估计方法相比较,估计信道矩阵的秩随时间的变化曲线如图3所示。

图3 估计信道矩阵秩的变化曲线Fig.3 Changing curve of the estimated channel matrix’s rank

从图3中可以看出,当信道估计过程中使用随机反射系数配置时,估计信道的秩随着发送导频数目增加而增大,增大到M=16时不再发生变化。当信道环境为无噪声的理想情况时,如果一直使用局部最优反射系数的配置,则信道估计结果始终保持不变,其秩恒为1。但实际的信道环境中总是存在噪声,由于噪声的随机性,即便RIS配置相同的反射系数,对应的接收信号亦不同。此时估计信道矩阵的秩虽然仍会增大,但并非持续性的过程,而是如红色曲线所示的间断性过程。所以为了避免估计信道秩亏,在估计过程中不能为RIS配置局部最优反射系数,而要配置第3.2节中的混合反射系数。

4.2 信道估计归一化均方误差

在配置混合反射系数时,式(18)中归一化权重的大小对信道估计结果极为重要。本文在仿真中为取了4个不同的值,分别为0.3、0.5、0.7、0.9,并将传统的随机反射系数配置方法作为基准,对其各方面的性能进行了比较。

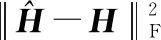
图4在信道信噪比设置为20 dB的情况下,对各算法的NMSE性能进行了仿真,并将文献[10]所提出的信道估计算法与本文算法作了比较。在该文献中,不同时刻的反射系数组成一个离散傅里叶变换矩阵,因而反射系数亦处于特定配置状态。可以看出,在信道估计的初始阶段,文献[10]算法的估计准确度较低。但随着时间增加,估计准确度迅速提升,这是因为该算法是一次性信道估计,只需要在==256的时刻计算估计信道,在后面的时刻中无法再提升估计信道的准确度。而本文的算法属于渐进信道估计,在>=256的时刻仍可以继续提高信道估计的准确度,并达到与文献[10]算法相持平的估计效果。同时,采用文献[10]中的反射系数配置亦无法增大接收功率并减少导频开销,这一结论可从下一节的对比仿真图中获得。

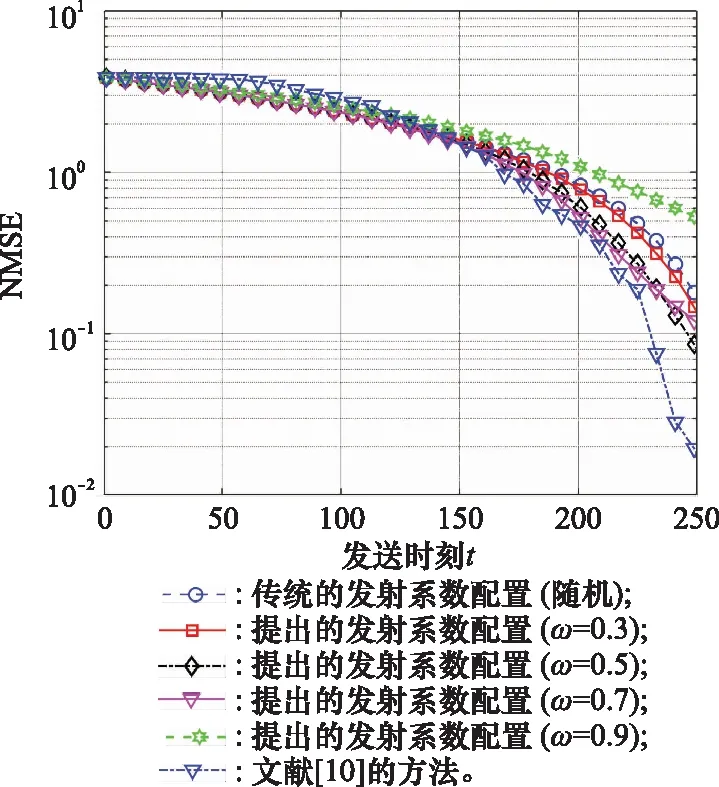
图4 不同算法下的NMSEFig.4 NMSE of different algorithms

从不同的来看,在取值为0.9时,由于配置的混合反射系数更偏向于局部最优反射系数,其估计信道会出现秩亏倾向,估计误差仍然较大,NMSE性能低于取值较小时的算法配置。在取值为0.7时,混合反射系数中局部最优反射系数的占比仍然较大,随着时间的增加,其NMSE下降的速度在减缓。当取值为0.3和0.5时,由于混合反射系数中随机反射系数的占比较大,估计信道不会出现秩亏倾向,且少量的局部最优反射系数能够使信道估计过程中的接收端信噪比增大,让接收信号更接近于发送信号,故此时的信道估计结果既优于局部最优反射系数的配置,也优于随机反射系数的配置,证明了本文提出的混合反射系数配置方法的优越性。

4.3 归一化接收功率

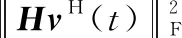
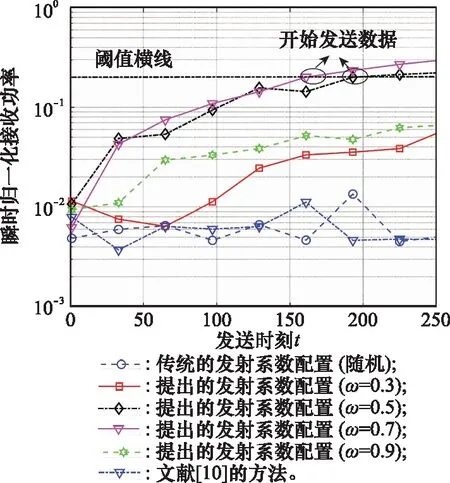
图5 瞬时归一化接收功率(SNR=0 dB)Fig.5 Instantaneous normalized received power (SNR=0 dB)

图6 瞬时归一化接收功率(SNR=10 dB)Fig.6 Instantaneous normalized received power (SNR=10 dB)

这里假设数据传输的阈值为0.2,即当瞬时接收功率达到最大接收功率的0.2倍时即可开始传输数据。从图5和图6可以看出,在信噪比为0 dB的情况下,取值分别为0.5和0.7时,发射端可提前开始发送数据;在信噪比为10 dB的情况下,取值分别为0.5、0.7、0.9时,发射端可提前开始发送数据,且开始数据传输的时刻比0 dB条件下更早,说明信道信噪比越大,所提算法性能越好。但在单次信道实现的仿真条件下,()的波动较大。因此,本文在给定信噪比为10 dB的条件下,分别对100个不同信道的()进行了仿真,最后将多个()结果曲线进行平均,得到平均归一化接收功率图,如图7所示。

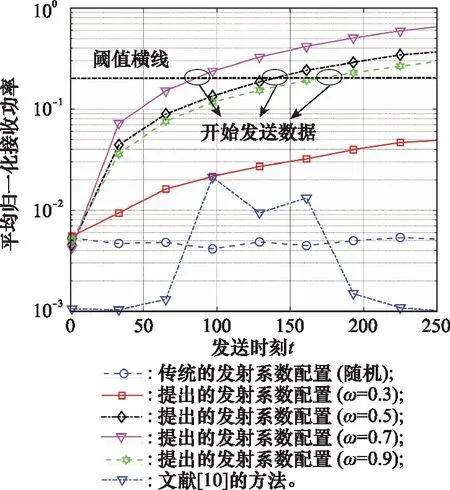
图7 平均归一化接收功率(SNR=10 dB)Fig.7 Average normalized received power (SNR=10 dB)

从图7中可以看出,当反射系数为随机配置时,瞬时接收功率远低于最大接收功率,且处于波动状态。当采用文献[10]中的特定反射系数配置时,瞬时接收功率仍然远低于最大接收功率,因而必须在信道估计完成后才能开始发送数据。

当=0.3时,瞬时接收功率已呈现出稳定增加的趋势,但由于混合反射系数中随机反射系数所占的权重更大,其增长幅度较小;当取值分别为05、07、09时,瞬时接收功率已经有了更为稳定的增长幅度。特别地,当=07时,混合反射系数中局部最优反射系数的权重略高于随机反射系数的权重,不仅可以保证信道估计结果的准确度,也能让瞬时接收功率以较大幅度增长,其在=100之前的时刻即可开始发送数据,在信道估计过程中可以减小更多的导频开销。

从本节的3个仿真图中可以看出,混合配置算法能使接收功率单调增长,而随机配置算法及文献[10]的算法的接收功率却处于波动状态。其次,接收端可以根据不同的功率阈值来确定开始传输数据的时刻,提前传输数据在一定程度上减小了导频开销,这是本文算法的优势之一。同时也可以看出,归一化权重的取值至关重要,因此下一小节将着重分析的变化对算法性能的影响。

4.4 归一化权重值对性能的影响

根据第32节中提出的信道估计算法,局部最优反射系数及归一化权重的配置会影响信道估计结果,而估计结果又会影响下一时刻局部最优反射系数的计算,同时估计结果本身还受到信噪比等参数的影响,因此要从理论分析中获取最优归一化权重值是较为困难的。本节中选取反射单元个数以及信噪比两个参数,从仿真实验来分析其对最优归一化权重值的影响。

假设瞬时接收功率达到最大接收功率的02倍时即可开始传输数据,设开始传输数据的时刻为,则定义归一化数据传输时刻为×100%。归一化数据传输时刻的值越小,对应的归一化权重值越接近于最优归一化权重值。图8在给定信噪比为10 dB的条件下,分别将取值为64、128、192、256、320,并对不同归一化权重取值下的归一化数据传输时刻进行了仿真。

图8 不同反射单元个数下的最优归一化权重值Fig.8 Optimal normalized weight value under different number of reflection elements

从图8中可以看出,随着的增大,最优归一化权重值稳定在0.7附近,说明不同的反射单元个数对最优归一化权重的取值并无较大影响。

图9在给定反射单元个数为256的条件下,分别将信噪比取值为5 dB、10 dB、15 dB、20 dB、25 dB,对不同归一化权重取值下的归一化数据传输时刻进行了仿真。从图9中可以看出,不同的信噪比对最优归一化权重值有一定的影响,如当信噪比为5 dB和15 dB时,其最优归一化权重值在0.65左右,当信噪比为20 dB和25 dB时,其最优归一化权重值在0.75左右。故对本文提出的算法而言,要找到一个非常确切的最优归一化权重值是较为困难的,因为其与通信系统的信噪比等参数相关。

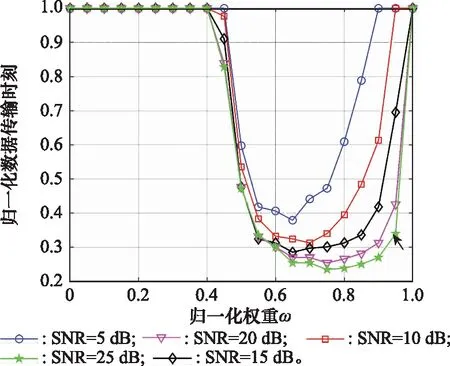
图9 不同信噪比下的最优归一化权重值Fig.9 Optimal normalized weight value under different SNR

但从图8和图9的分析结果来看,可以将=0.7作为平均意义下的最优归一化权重值,这样即可保证所提算法性能较优。

4.5 归一化接收功率的互补累积分布函数

在任意发送时刻,归一化接收功率是一个随机变量,本节研究该随机变量的互补累积分布函数(complementary cumulative distribution function,CCDF)。定义归一化接收功率在时刻大于阈值的概率为

CCDF(,)={()>}

在给定信噪比为10 dB的条件下,本文通过仿真实现了100个不同的信道,并分别对取值分别为0.1、0.3、0.5情况下的CCDF曲线进行了仿真,如图10所示。

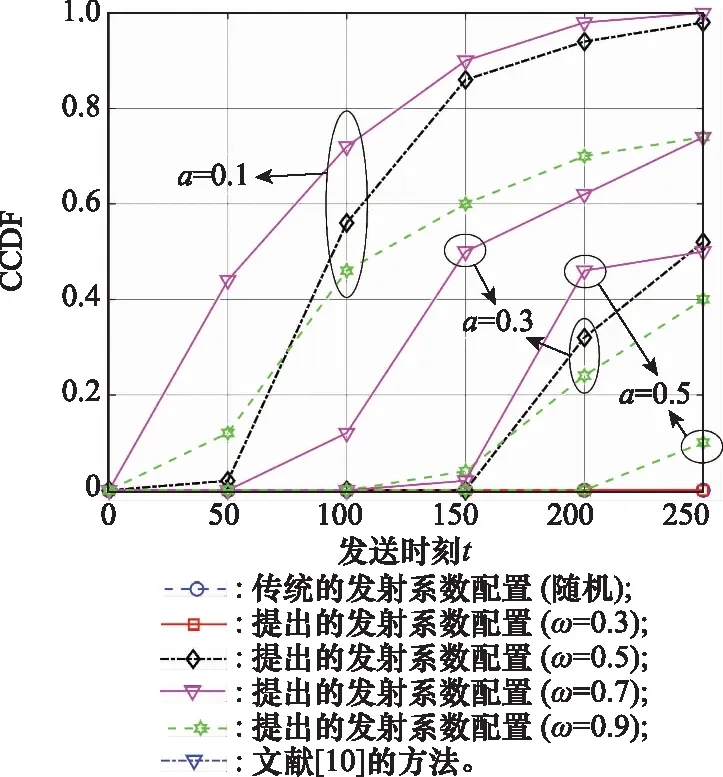
图10 不同阈值下的CCDFFig.10 CCDF under different thresholds

从图10中可以看出,阈值越小,则达到该阈值的概率越大。随着阈值的增大,达到该阈值所需的时间越长,CCDF曲线随着发送时刻向后偏移。当=0.3时,由于混合反射系数中局部最优反射系数占比较小,归一化接收功率上升速度缓慢,在3个不同的阈值下其CCDF取值均为0。当=05时,在=100及之后的时刻,归一化接收功率均有较大的概率达到0.1的阈值,但当阈值增大至0.5时,其CCDF为0,说明=05算法所能达到的阈值上限较低。相比之下,当取值分别为07和09时,其归一化接收功率增长幅度大,所能达到的阈值上限较高,如在=200的时刻,=07的算法有接近一半的概率达到05的阈值。本节的仿真结果仍然表明了将取值为07是保证算法性能的一个较优选择。

4.6 导频开销

在文献[10]的RIS信道估计方法中,第个时刻即可完成信道估计,并让发射端开始传输数据。而在本方法中,发射端根据接收信号功率阈值来传输数据,设开始传输数据的时刻为,则其归一化后的导频开销百分比为×100%。图11对不同取值下的归一化导频开销进行了仿真。其横轴为对应的归一化接收功率阈值,若达到该阈值即可发送数据。可以看出,由于=07时瞬时接收功率的上升速度最快,故归一化导频开销最小。当阈值较低时(如阈值为01和02),取值分别为07和09的算法均可减小一半以上的导频开销。随着阈值的增大,开始传输数据的时刻越来越迟,归一化导频开销也随之上升。相较于传统的随机反射系数配置方法,本文所提出的方法能够有效减少导频开销,使发射端尽早传输数据。

图11 不同阈值下的归一化导频开销Fig.11 Normalized pilot overhead under different thresholds

5 结 论

基于RIS辅助的通信系统,本文提出了一种与反射系数配置相结合的渐进式信道估计方法。在信道估计过程中,利用非完整信道信息来计算该条件下的最优反射系数,并为RIS配置由最优反射系数和随机反射系数组成的混合反射系数,再更新非完整信道信息。随着发送导频数目的增加,信道估计结果越来越接近于真实信道,接收信号功率也逐步增加。仿真结果表明,混合反射系数中最优反射系数的归一化权重对算法的性能至关重要,当取值较小时,信道估计结果准确度较高;当取值较大时,可使发射端尽早开始传输数据。在实际系统中应用时,应将取值为07,使估计结果与接收功率处于一个平衡的状态,让算法发挥出更优的性能。