一道立体几何高考题的多种解法
2020-12-15江西省高安市第二中学330800张克勤
中学数学研究(江西) 2020年12期
江西省高安市第二中学 (330800) 张克勤
2020年全国Ⅰ卷数学(理)第18题,由于该题考查的图形是立体几何中的圆锥,可以非常好的选择建立空间直角坐标系来解决该题的第(2)问,本文给出不同于参考答案的另外两种解法.
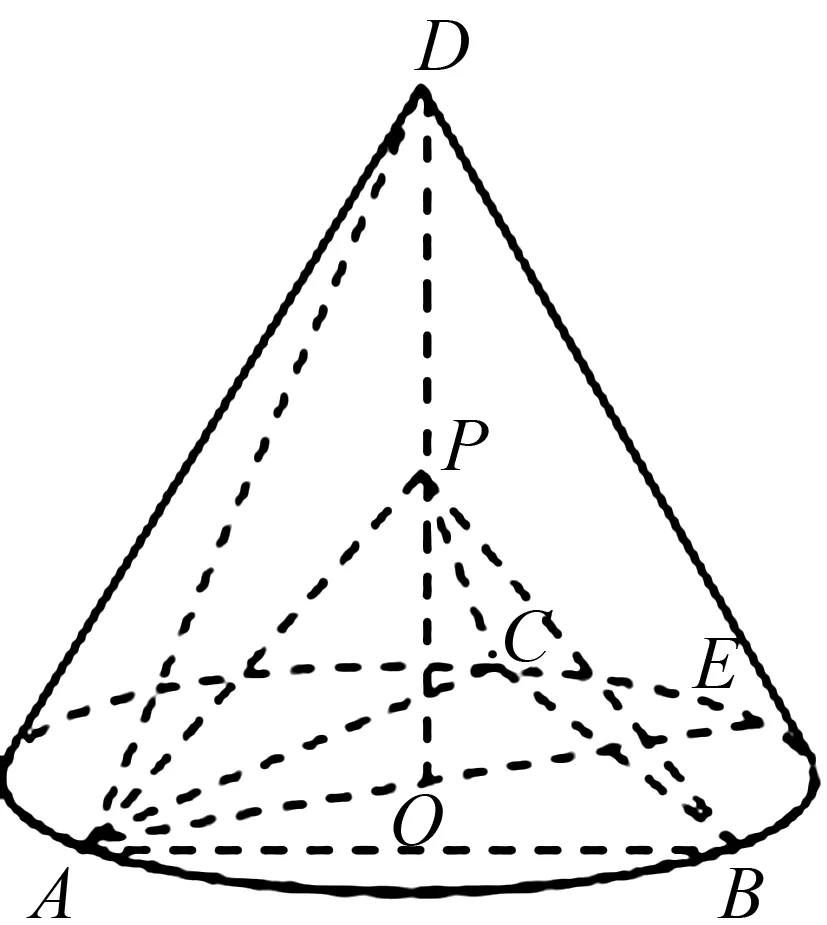
图1

(1)证明:PA⊥平面PBC;
(2)求二面角B-PC-E的余弦值.

图2

E(-2a,0,0),所以
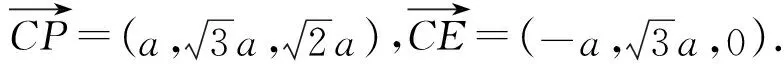

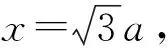
评注:解法一是命题者提供的参考答案,通过建系,利用空间向量关系求解,解法自然常规,但运算量较大.

图3

评注:解法二是利用向量的数量积的定义求解.相对解法一更加简化,无需建系求坐标,但用到向量的加减运算和数乘以及二面角平面角的定义,这些也是教材中的基础内容.

图4

评注:解法三直接利用余弦定理,无需建系求坐标,也不需要用到向量的加减运算和数乘,但要求在空间图形中寻找到二面角相应的平面角,这正是回归立体几何教学的本位,更凸观立体几何教学的核心素养目标.
