解析几何两类问题的拓广

江西省抚州市临川区第十六中学 (344100) 邓在祥

1.引言

关于点到直线的距离公式，笔者曾经看过如下推导方法.

问题已知直线l:Ax+By+C=0，点P在直线l外，求点P到直线l的距离.

图1

解：设f(x,y)=Ax+By+C，则f(x,y)=

A(x-x0)+B(y-y0)+Ax0+By0+C=A(x-x0)+B(y-y0)+f(x0,y0).

如图1，过P作PH⊥l于H.

①当A,B均不为零时，

②当A,B有且只有一个为零时，易验证公式(*)仍然成立.

这里，将直线方程中的x,y分别换成x-x0,y-y0，却能使公式的推导过程大为简化，不能不令人称奇.受此启发，笔者尝试利用这种想法去解决其他一些相关问题，发现有不少问题也有类似的效果.值得一提的是，这种想法能方便解决解析几何中许多“传统问题”的拓广形式.本文仅举两例说明.

2.中点弦问题的拓广

在解析几何中，凡是涉及到圆锥曲线弦的中点问题，都被称为“中点弦问题”，如

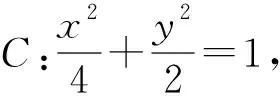
这是一道典型的中点弦问题，常规的解法是“韦达定理法”和“点差法”.现将该问题拓广为

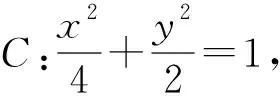
拓广后的问题即为圆锥曲线弦的定比分点问题.对于此类问题，如用问题1的解法求解就不灵便了.

3.对称问题的拓广

对称问题是直线与圆锥曲线位置关系问题中的一种典型问题，如

解决此类问题的基本方法也是韦达定理法和点差法.现将该问题拓广为

图2

下面是问题4的一种解法.

解：设PQ:y=-x+b，P(x1,y1),Q(x2,y2),M(x0,y0)，则有f(x,y)=x2+2y2-2=(x-x0)2+2(y-y0)2+2x0(x-x0)+4y0(y-y0)+f(x0,y0)，g(x,y)=x+y-b=(x-x0)+(y-y0)+g(x0,y0).

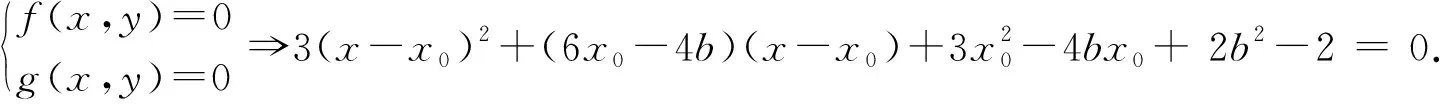
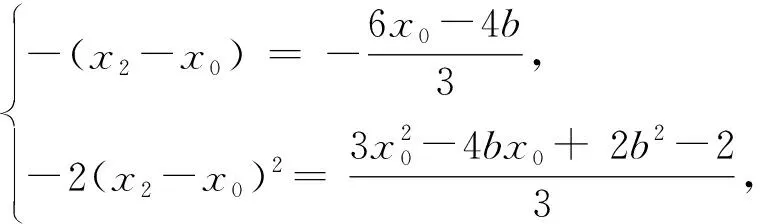
b-3(-3,2717)2717(-2717,3)3u'(b)-0+u(b)33↘-51↗-33