基于Bathe积分算法的机械系统多体动力学方程求解方法
2020-12-15钱林方陈光宋
吉 磊, 钱林方, 陈光宋, 尹 强
(南京理工大学 机械工程学院,南京 210094)
多体系统动力学有多种建模手段[1-3],如绝对坐标法[4]、相对坐标法[5]、凯恩方法[6]和递推方法[7],很多学者[8-10]对这些建模方法进行了研究.对于一般含完整约束的多体系统,采用上述任一方法并引用拉格朗日乘子,均可建立一组微分代数方程(DAEs),从而利用各种数值方法进行求解.然而DAEs不同的指标或形式有可能对数值方法的求解与效率产生影响,因此当采用不同的数值方法时,需要考虑DAEs的形式以适应算法,从而高效准确求解.
多体系统动力学方程的数值求解算法一直是多体问题中的关键内容,国内外学者研究了各种数值算法用于多体动力学方程的求解:Negrut等[11-12]提出了求解指标-3的多体系统动力学方程的Newmark方法和HHT-I3方法;Jay等[13]对广义-α法进行了扩展研究,使其能够对包含变质量矩阵、完整约束和非完整约束的多体系统进行求解运算,同时还提出了新的变步长公式;Lunk等[14]扩展了Newmark方法和广义-α法类的方法用于求解含约束的机械系统,通过联立位移和速度的稳定项从而保证约束正确,使用的α-RATTLE方法具有二阶精度;Shabana等[15]提出了使用Newmark法对独立坐标积分的双循环隐式积分方法.马秀腾等[16-17]利用θ1方法分别求解了指标-3和指标-2的多体动力学方程,表明该方法具有2阶精度,并对HHT-SI2方法进行了改进,将其校正项通过两种不同方式进行改进,数值算例表明改进方法都具有二阶精度且数值阻尼可控;郭晛等[18]对HHT-α法在求解含接触约束的柔性多体系统动力学方程时的数值特性进行了研究;姚廷强等[19]运动广义-α方法计算分析了不同工况下圆柱滚子轴承的动态特性和保持架的稳定性,获得了不同工况下轴承动态响应的变化规律;丁洁玉等[20]基于广义-α法,结合约束投影方法构造了广义-α-S投影法,该方法能较好地保持系统总能量和满足约束,计算效率较高;刘颖等[21]提出了一种基于离散零空间理论的Newmark积分算法,结果表明该算法能够实现系统降维并提升效率.上述这些常用的求解算法已被用于多体系统动力学分析,而Bathe积分策略[22-23]作为一种二阶隐式积分算法,最初主要针对结构动力学常微分方程组(ODEs)的积分求解,而其亦可推广到对DAEs的求解.Bathe积分算法的优点在于求解长时间历程的非线性动力学问题时比较稳定,数值耗散较小,在较大积分步长的情况下也能获得较好的精度.
本文将传统的多体系统动力学方程整理为显含广义阻尼矩阵的形式,为Bathe积分算法提供高效计算的基础.采用Baumgarte约束稳定法在动力学方程中添加了约束稳定项,减小约束违约对系统响应的影响.推导了利用Bathe积分算法求解动力学方程的计算过程,将广义阻尼矩阵应用于迭代求解时的初值计算以提高效率.最后利用算例验证了Bathe积分算法求解多体系统动力学方程的准确性和使用显含广义阻尼矩阵形式计算的高效性.
1 多体系统动力学方程一般形式
1.1 多体系统运动学方程
建立多体系统的运动学方程[24],首先需推导两个相邻刚体的运动学关系.两个相邻刚体之间的运动关系如图1所示,图中O0x0y0z0为参考坐标系,Oixiyizi和Ojxjyjzj为分别为Bi和Bj刚体上的连体坐标系,piOξiOηiOζiO和pjIξjIηjIζjI为铰Jj分别与Bi和Bj两个刚体相连处的坐标系.

图1 相邻刚体位置关系
假设体Bi和Bj的连体坐标系Oixiyizi和Ojxjyjzj相对参考坐标系O0x0y0z0的速度与加速度矢量分别为
(1)

根据相对坐标法可递推得到体坐标系运动矢量与铰坐标系相对运动矢量之间的关系:
(2)
(3)
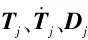
(4)
(5)

1.2 多体系统动力学方程
对于任意刚体Bi,假定ci为体内任意一点相对连体坐标系Oixiyizi的矢径,则可得该点的加速度为
aci=ai+εi×ci+ωi×(ωi×ci)
(6)
式中:ai为Oi相对参考坐标系O0x0y0z0的加速度.
根据虚功率原理,可得到该体的虚功率方程为
(7)

δvci=δvi+δ(ωi×ci)
(8)
将式(1)、(2)、(6)分别代入式(7),并将单体的虚功率方程运用至多体系统中,整理成紧凑形式得
(9)
式中:R、W、E、Qa和Qn为式(7)中各项在整个多体系统中的整合形式.
将式(4)和(5)代入式(9)可得
(10)
由于约束力和力矩不做功,所以其虚功率为0,将式(10)写成紧凑形式得
(11)
(12)
根据变分原理可得系统动力学方程为
(13)
当多体系统中包含完整约束时,通过引入拉格朗日乘子λ写出带约束的动力学方程:
(14)
式中:Φ(q,t)=0为系统约束方程;Φq为Φ(q,t)对q求导.将式(14)中的约束方程Φ(q,t)=0对时间t求二阶导数,可将式(14)写为如下指标-1的微分-代数方程组:
(15)
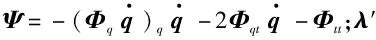
1.3 Baumgarte约束违约稳定法
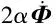
(16)
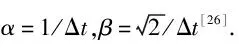
(17)
式中:λ″为λ对时间的二次积分项(λ″并未参与计算,引入λ″同样是为了保持方程形式的一致性),则式(16)可整理为
(18)
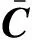
2 Bathe积分用于求解多体系统动力学方程
Bathe积分的求解思路是已知t时刻的运动参数和计算步长Δt,待求t+Δt时刻的响应,通过引入参数γ,先计算t+γΔt时刻的响应,再利用t和t+γΔt时刻的响应计算t+Δt时刻的响应,从而完成一个时间步长的求解.

(19)
(20)
(21)
(22)
t+γΔt时刻的动力学方程为
(23)
将式(21)和(22)代入式(23),可得
(24)
即为t+γΔt时刻以Pt+γΔt为自变量的动力学方程.
获得t+γΔt时刻的运动参数后即可计算t+Δt时刻的运动参数.在t+Δt时刻的函数f的导数可写为t、t+γΔt和t+Δt时刻函数的组合形式[22]:
(25)
(26)
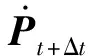
将式(27)代入式(28),可得
c2c3Pt+γΔt+c3c3Pt+Δt
(29)
t+Δt时刻的动力学方程为
(30)
将式(27)和(29)代入式(30)可得
(31)
即为t+Δt时刻以Pt+Δt为自变量的动力学方程.
式(24)和(31)都可通过Newton迭代方法进行求解,为提高计算效率采用Broyden拟牛顿法,迭代过程如下:
(32)
式中:上标k和k+1分别表示第k次和第k+1次迭代;下标tCalu表示当前计算的时刻(tCalu=t+γΔt或tCalu=t+Δt);yk和sk都为迭代的中间变量;J表示雅克比矩阵;Y的表达式如下:
(33)
根据泰勒展开原理,式(24)的迭代初值可设置为
同理,式(31)的迭代初值可设置为
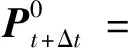
(36)
(37)

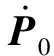
3 数值算例
3.1 曲柄滑块机构
下面以曲柄滑块机构为例,验证Bathe积分算法求解多体系统动力学方程的准确性和高效性.如图2所示,图中曲柄、连杆和接触体均为均质实心圆柱体,点O1、O2和O3分别为曲柄、连杆和滑块的质心.Oxy为参考坐标系,局部坐标系O1x1y1、O2x2y2和O3x3y3与3个构件质心固接,θ1和θ2为曲柄和连杆的转动角.滑块末端与弹簧阻尼机构相连,刚度为k,阻尼为c.当θ1和θ2为0时,该弹簧处于平衡位置.图中l1和l2分别表示曲柄和连杆的长度,m1、m2和m3分别表示曲柄、连杆和滑块的质量,各参数取值如表1所示.假设系统只受重力作用,重力加速度g=9.806 65 m/s2.
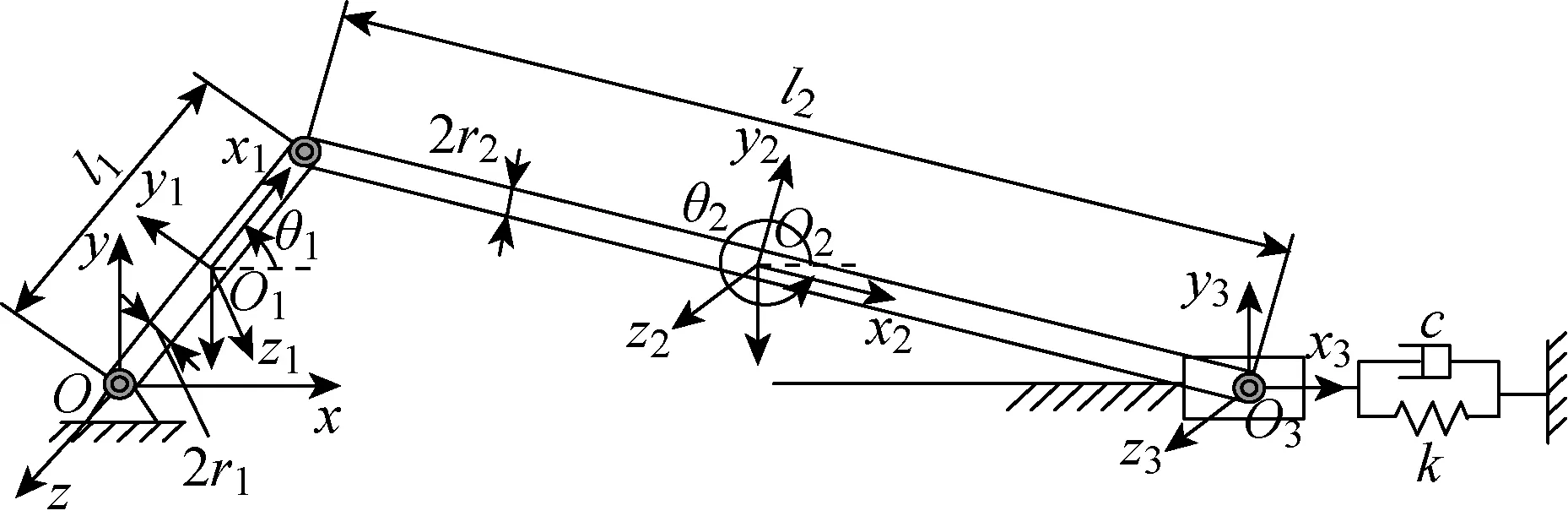
图2 曲柄滑块示意图

表1 曲柄滑块参数列表
由于本算例无解析解,所以本文利用Adams软件中的WSTIFF积分器SI2算法作为求解算法,误差设置为10-10,步长设置为10-6,以此情况下的结果作为参考解.下面给出了Bathe算法与Adams计算出的参考解对比,图3和图4分别为θ1、θ2随时间变化的曲线图.

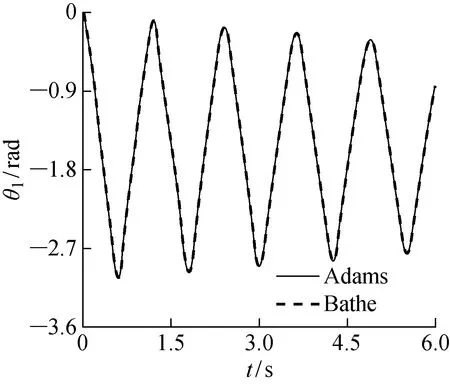
图3 θ1随时间变化曲线

图4 θ2随时间变化曲线
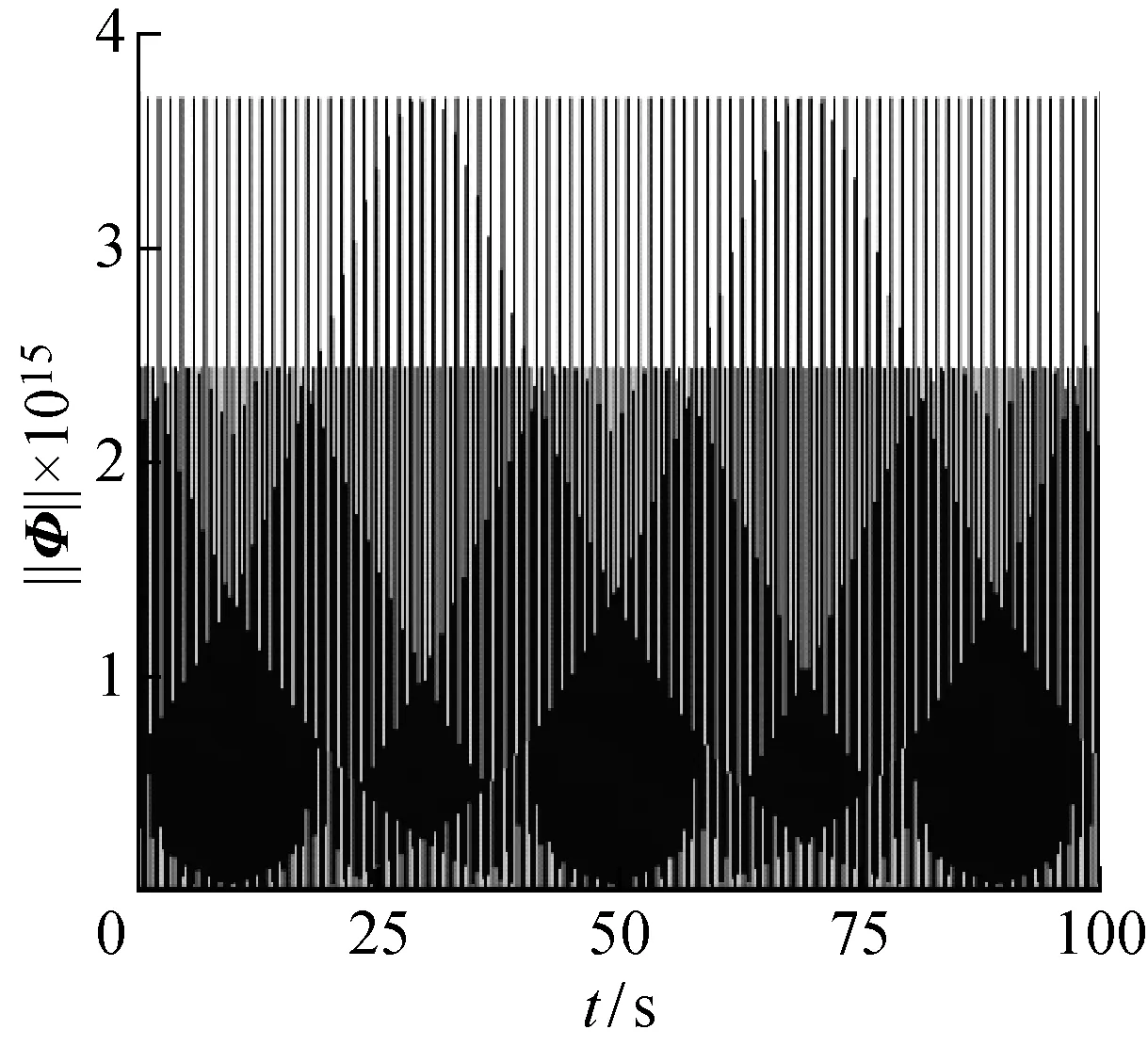
图5 位移约束方程违约值
为了研究Bathe积分算法对系统总能量(包括动能、重力势能以及弹簧的弹性变形势能)的影响,假设弹簧阻尼c=0,图7显示了不同γ取值(0.1、0.3、0.5、0.7和0.9)时系统总能量保持的情况,从图中可看出γ=0.1与γ=0.9时较为一致,γ=0.3与γ=0.7时较为一致.不论γ取值,总能量的变化范围都较小,Bathe积分算法较稳定且数值耗散较小,在本文中,如不特别说明,γ取值为0.5.

图6 速度约束方程违约值曲线

图7 系统总能量随时间变化曲线

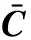
表2 雅克比矩阵的初值J0中是否含有广义阻尼矩阵对Bathe算法总迭代次数的影响
使用Adams软件以10-6为时间步长时的结果作为参考值,对比Bathe算法与龙格库塔45阶算法(RK45)对θ1和θ2的计算结果在不同时间步长Δt(0.05~10-5s)情况下的相对误差e情况以及相应CPU时间(tCPU),对比结果如图8~10所示(图中均为双对数坐标).

图8 θ1的相对误差随时间步长的变化

图9 θ2的相对误差随时间步长的变化
从图8和9中可以看出:在相同的时间步长下,Bathe算法计算结果的相对误差较小,收敛效果更好;且随着步长的减小,Bathe算法相对误差下降的趋势更加显著.从图10中可以看出:相同时间步长下Bathe算法的计算耗时比RK45算法稍长,这是由于Bathe算法每个时间步长都需要进行迭代计算至收敛的原因;且随着时间步长的减小,两种算法计算的CPU时间有相互接近的趋势.若兼顾精确度与计算CPU时间,选择Bathe算法进行动力学计算对计算耗时的略微牺牲能获得更精确的计算结果.

图10 计算的CPU时间随时间步长的变化
3.2 含接触的曲柄滑块
以含接触的曲柄滑块机构为例,验证Bathe积分求解算法对含接触的多体系统同样适用.如图11所示,曲柄滑块机构与算例3.1中的相同,在此基础上添加一接触体,接触体与地面固连,在系统运动过程中与连杆发生接触,接触体为均质实心圆柱,点O4为其质心,坐标系O4x4y4z4固接于接触体质心,r4、l4和m4分别表示接触体的半径、长度和质量.选择使用纯弹性接触力模型模拟刚体之间的接触碰撞过程.接触力Fc的模型[27]为
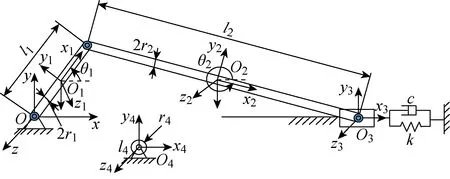
图11 含接触的曲柄滑块示意图
(38)
式中:δ为穿透深度;Kc为接触刚度;nc为接触指数.算例中参数取值如表3所示(其余参数与表1一致),假设系统只受重力作用.

表3 接触体及接触力参数
采用本文的建模方法建立动力学方程,并采用Bathe算法计算0~2 s内该系统的响应,Bathe积分策略参数λ=0.5,步长取10-5s,初始状态时θ1和θ2为0.下面给出了Bathe算法与Adams软件计算的结果进行对比,图12和13分别为θ1和θ2随时间变化的曲线图.同算例3.1一样,从图12和13中可以看出Bathe积分算法求解的结果与Adams软件求解的结果是一致的.图14和15给出了接触力在x方向和y方向的曲线图,显示两种算法结果一致,每次接触开始和结束的时刻以及力的大小都一致,验证了Bathe积分策略用于求解含接触多体动力学方程同样是有效和准确的.
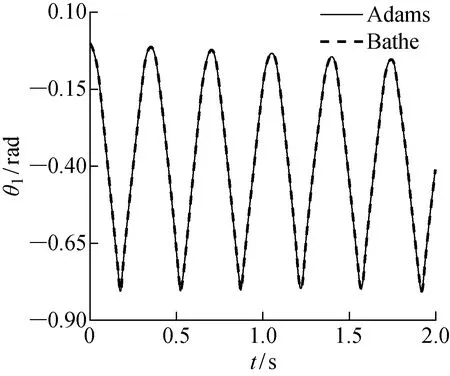
图12 θ1随时间变化曲线
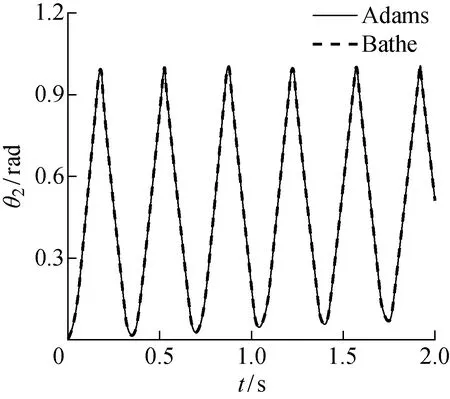
图13 θ2随时间变化曲线
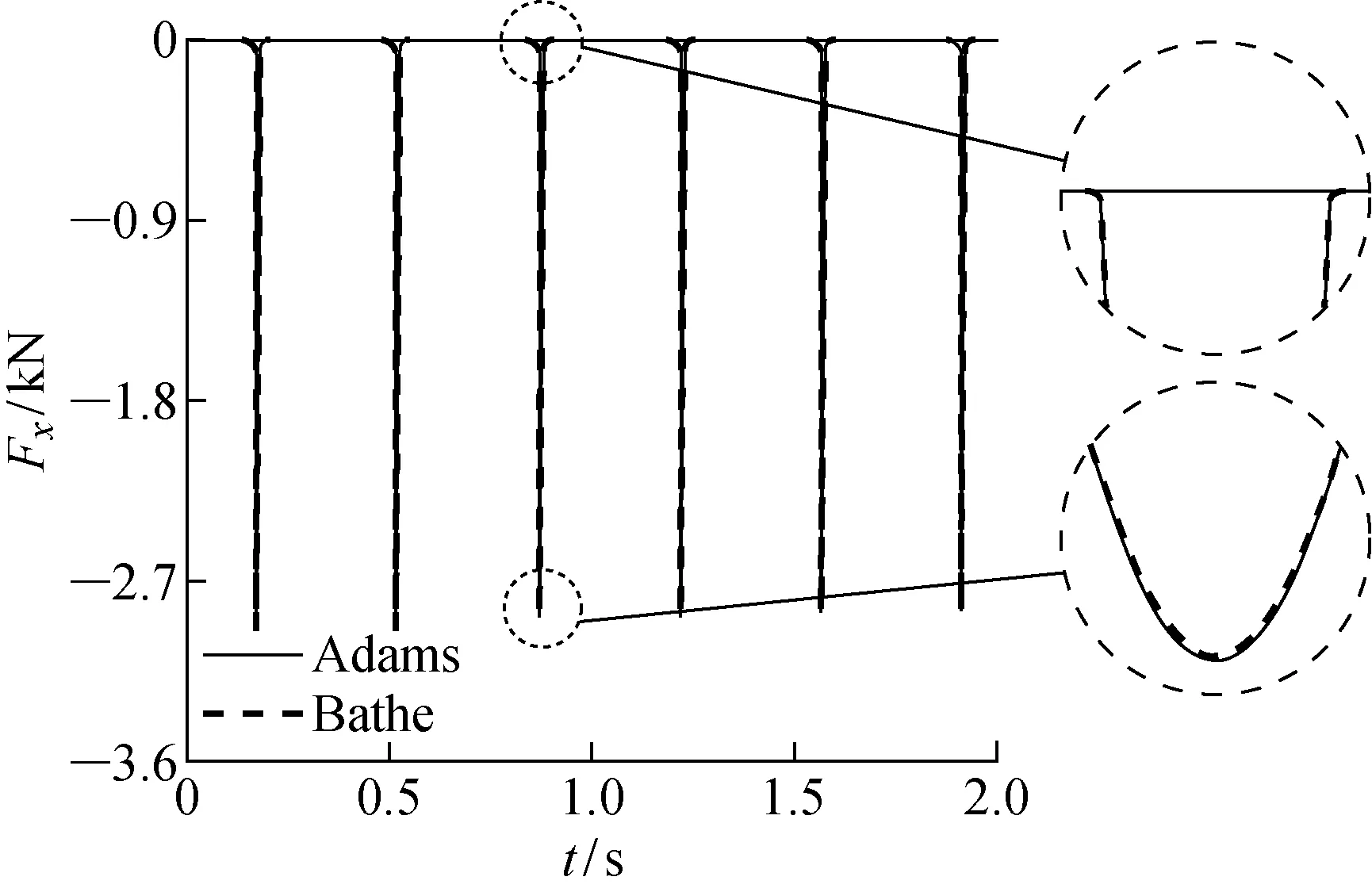
图14 接触力在x方向上随时间变化曲线
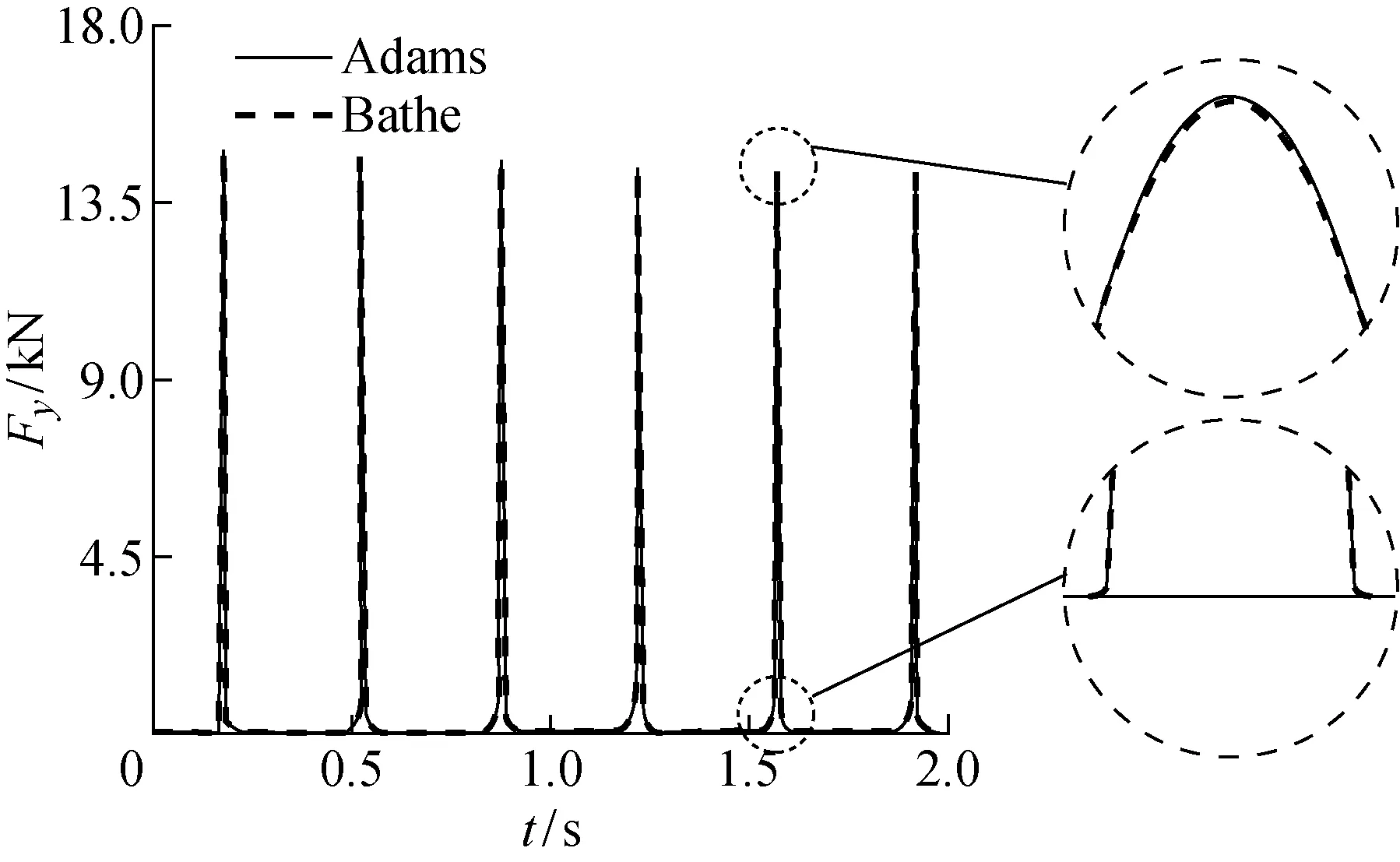
图15 接触力在y方向上随时间变化曲线
4 结论
本文主要研究了Bathe积分算法在多体系统动力学中的应用.将多体系统动力学方程整理成显含广义阻尼矩阵的形式,并在动力学方程中添加了Bamugarte违约稳定项,推导了Bathe积分算法求解多体系统动力学方程的具体流程,将广义阻尼矩阵用于迭代计算时选取雅克比矩阵的初值.通过数值算例,得到如下结论:
(1)利用Bathe积分算法求解多体系统动力学方程具有准确的结果,约束违约值很小,算法稳定性较好.Bathe积分算法求解时的数值耗散小,不同γ参数时总能量的变化规律略有区别.
(2)由于将动力学方程整理为显含广义阻尼矩阵的形式,改进了雅克比矩阵迭代初值的选择,提高了Bathe积分算法的计算效率,且随着步长的增大计算效率相对越高.
(3)Bathe算法在相同步长情况下的计算结果更加准确,收敛性更好.虽然Bathe算法计算时的CPU时间会略微变长,但计算结果的准确性会大幅度提高.
