基于在线加权慢特征分析的故障检测算法

黄 健， 杨 旭

(北京科技大学 自动化学院；工业过程知识自动化教育部重点实验室，北京 100083)

在现代工业中，生产过程安全和产品质量是最为关注的两个问题，随着生产规模的扩大和过程变量的增加，现代工业对过程监控提出了较高的要求[1-6].近年来，多元统计过程监测引起了广泛的关注，其主要思想是将高维数据投影到低维空间，并保留原始数据的主要信息[1-2, 7].在目前的研究中，最常用的多元统计方法是主成分分析(PCA)和独立成分分析(ICA)[3, 8-10].

传统的多元统计方法(如PCA和ICA)，通常认为其统计过程处于静态，过程当前时刻的状态不受之前时刻的影响.然而，在实际工业过程中，当前时刻几乎不会保持稳定状态，从而使过程变量呈现动态特性.因此，传统的监测模型无法明确表达过程数据的动态特性.Ku等[11]在模型构建过程中采用时滞变换策略来改善动态特性.Huang等[12]提出了结合动态PCA、动态ICA和Bayesian推理的动态过程监测方法.然而，动态过程的时变特性可能对不同的变量产生不同的影响，基于扩展矩阵的方式无法从根本上克服过程的动态特性.慢特征分析(SFA)[13-14]是一种无监督学习算法，其优化目标是提取随时间变化的慢特征.Shang等[13]指出动态性是表征过程变化的重要指标.Shang等[14]提出一种自适应过程监控的递归SFA算法，该算法通过更新模型参数和监控统计信息来自适应时变过程.Guo等[15]提出了概率SFA过程监测算法.Zhang等[16]将核SFA算法用于非线性间歇过程监测.上述研究采用SFA进行过程监测，取得了良好的监测结果.但是，这些文献几乎没有讨论如何在降维步骤中选择与故障相关的信息.

与此同时，生产过程监测需要建立可靠的模型.在基于数据的思想进行建模时，特征数据的选择对监测模型的准确性有着至关重要的作用.当前有很多算法应用于特征选择，汪嘉晨等[17]在关于对轴承技术参数的诊断问题中，提出一种用模型判断特征并通过阈值进行特征选择的方法.利用标准数据集进行离线训练，训练完成后利用所选择的特征构造统计量进行故障检测等工作.然而在实际工业过程中，特征空间并非保持一成不变，因此，离线建立的系统模型不能很好地反映每个采样时刻的系统性能，无法根据离线建立的系统模型对每个样本的状态进行准确地故障检测.Zhou等[18]提出一种基于自适应密度邻域关系的新在线流特征选择方法，即在进行在线选择的过程中，忽略过程的动态信息.Huang等[19]提出了基于在线特征重排和特征选择的慢特征分析故障检测算法，但在选择故障信息方面仍有不足.因此，深入研究凸显过程中的故障信息是非常重要的.

本文针对传统算法在监测动态过程中产生的未充分利用故障信息的问题，提出在线加权SFA故障检测算法.采用SFA算法提取慢特征数据，为动态特征设计阈值.在进行在线监测时，将超过阈值的特征认为是较为明显的、可能包含故障信息的嫌疑特征，将这些嫌疑特征选择到主空间进行进一步监测.为了凸显故障信息，引入权重系数的统计量计算方法，根据特征数值的大小给所有的嫌疑特征值赋予不同的权重系数，并根据这些带有明显故障信息的嫌疑特征计算控制阈值，以达到提高算法故障检测率的目的.

1 慢特征分析

给定一个输入信号向量x(t)，SFA算法的目标是找到一个特征函数g(x)，使得特征变量s(t)=g(x(t))随时间的变化较慢.m维的输入信号在时间范围t∈[t0,t1]内可以表示为x(t)=[x1(t)x2(t)…xm(t)]T，采用g(x)=[g1(x)g2(x)…gm(x)]T和s(t)=[s1(t)s2(t)…sm(t)]T表示特征函数和慢特征，其关系表示为si(t)=gi(x(t))，i=1,2,…,m.SFA算法的优化问题由下式表示[13-14]：

(5)

式(1)表示的是SFA算法提取慢特征时间变化最小化的优化目标.

SFA算法从正常数据中提取缓慢变化的部分，对每个慢特征进行线性特征转化，此过程可以表示如下[13,19]：

(6)

i=1,2,…,m

式中：wi为负载向量.因此，所有的慢特征可以写成原始变量的线性组合形式：

s=Wx

(7)

式中：W为负载矩阵，

W=[w1w2…wm]T

进行SFA算法计算时，第1步是进行白化处理以消除变量之间的相关关系.使用奇异值分解实现白化操作，假设x(t)是原始数据，并且

R=〈x(t)xT(t)〉t

表示为其协方差矩阵，R的奇异值分解可以写为

R=UΛUT

(8)

式中：Λ和U分别为特征值对角阵和特征矩阵.白化矩阵可以写作Q=Λ-1/2UT.同时白化过程可由下式描述：

z=Λ-1/2UTx=Qx

(9)

结合式(7)和(9)，可以推导出

s=Wx=WQ-1z=Pz

(10)

这里P=WQ-1，显然有〈zzT〉t=Q〈xxT〉QT=I以及〈z〉t=0.又由于约束(2)和(3)的存在，可以得到下式：

〈ssT〉t=I

(11)

则式(11)可以写为

〈ssT〉t=P〈zzT〉PT=PPT=I

(12)

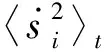
(13)

式中：pi为特征向量.实际过程中，样本数据是在离散的时间状态下采集到的.基于时间的导数可以由差分近似，计算如下：

(14)

式中：Δt为时间间隔.通过使用协方差矩阵的奇异值分解来解决优化问题，在这种情况下，奇异值分解可以表示为

(15)

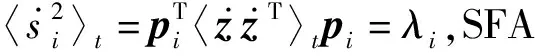
可知，负载矩阵的计算可以由下式表示：

W=PQ=PΛ-1/2UT

(16)

2 基于在线加权SFA算法的故障检测方法

2.1 特征降维和离线控制限计算

采集样本数据后，可以使用SFA算法提取过程中不同的动态水平特征.在实际动态工业过程中，故障可能发生在部分动态特征中，因此通过SFA算法进行动态特征提取时，需要选择重要特征对数据进行降维.由于SFA算法是一种线性的特征提取方法，通常认为权重矩阵中，具有较大L2范数的行对应慢特征能够捕捉到过程的变化.

若k个重要慢特征可表示为sk，采用S2和SPE统计量进行故障检测，两个统计量的计算如下：

(19)

式中：yi为来自数据集的观测值；n为样本数量；b为带宽；G(·)为核函数.选择核函数为Gaussian核函数，表达式如下：

(20)

2.2 选择在线嫌疑故障特征

在线特征选择时，故障嫌疑选择结果比较依赖于控制限的选择.如果控制限的选择过高，将导致故障相关特征数据挑选不足，容易忽略在线数据特征中包含故障信息的部分，导致最后的系统故障信息体现不明确，影响故障检测的正确率.相反地，如果控制限的选择过低，将会筛选出大量的未包含故障信息的冗余特征数据，这会降低故障相关特征数据的比重，也容易导致系统的故障信息体现不明确，进而影响故障检测结果.

在线特征选择利用离线计算的控制限对每个慢特征监控统计量进行逐个判断，将超出平均控制限的部分数据选择出来，认为其是有故障嫌疑的部分，将其放入主空间进行监测，计算统计量和控制限.选择条件如下：

(21)

式中：σ为松弛系数，σ∈(0,1].松弛系数的作用是放宽控制限的筛选严格度，避免控制限过高导致丢失故障信息.考虑到控制限的选择对故障检测结果有着较为重要的影响，为了避免控制限选取的过高而导致在线选择的特征数据有缺失，应给松弛系数赋予一个合适的值.

2.3 加权SFA故障检测方法

慢特征作为潜变量，包含了采样的过程变量的诸多信息.然而由式(21)可知，引入了松弛系数可能使得更多的慢特征被认定为嫌疑变量.如果特征选择过程中确定的控制限较低，将会导致有些筛选出来的特征是不含故障信息的，即筛选出很多冗余信息.这降低了包含故障信息的特征数据的比重，使故障信息的体现不明确，可能会导致无法有效地检测出故障.为了解决上述问题，凸显故障信息，在计算在线监测统计量时引入权重系数，即给每个特征赋予一定权重，将数值大的、可能包含更多故障信息的特征数据赋予较高的权值，而对数值小的、可能包含较少或不包含故障信息的特征数据赋予较低权值，将故障信息尽可能地突显出来.

(22)

(23)

3 仿真实验

3.1 数值系统仿真实验

此多变量的数值仿真系统是由Ku等[11]提出并经过Lee等[20]加以优化.系统如下所示：

(24)

y(q)=a(q)+v(q)

(25)

(26)

式中：输入h为随机向量，服从在区间(-2,2)上的均匀分布；输出y等于a加上随机噪声向量v；噪声v服从均值为0和方差为0.1的Gaussian分布；输入u和输出y都可测，a和h不可测.本文生成960个样本用于分析，每个样本包含5个变量(y1,y2,y3,u1,u2).用于监测的故障均是从第161个样本开始引入，即1～160的样本为正常数据，161～960的样本为故障数据，故障创建如下：

故障1h2处引入值为2的阶跃故障.

故障2h1引入0.01(q-160)的斜坡故障.

在进行特征选择时，利用传统SFA算法选择的离线特征不一定全是包含故障信息的特征.故障1的所有慢特征如图1所示，其中SF1～5代表特征1～5.由图1可知，特征1和4在故障发生时有明显的上升趋势，包含故障信息，而靠前的特征2和3并没有显示出明显的故障信息.嫌疑特征加权前后的统计量如图2所示.由图2可知，特征1、2、4是挑选出的故障嫌疑变量.权重系数对筛选出来的慢特征进行了权重赋值，特征1和4所占比重增加，使含有故障信息的特征数据体现地更加明显.所提出的在线特征选择的策略，可以挑选出包含故障信息最明显的特征，经过特征加权，凸显了故障信息.

图1 故障1的所有慢特征

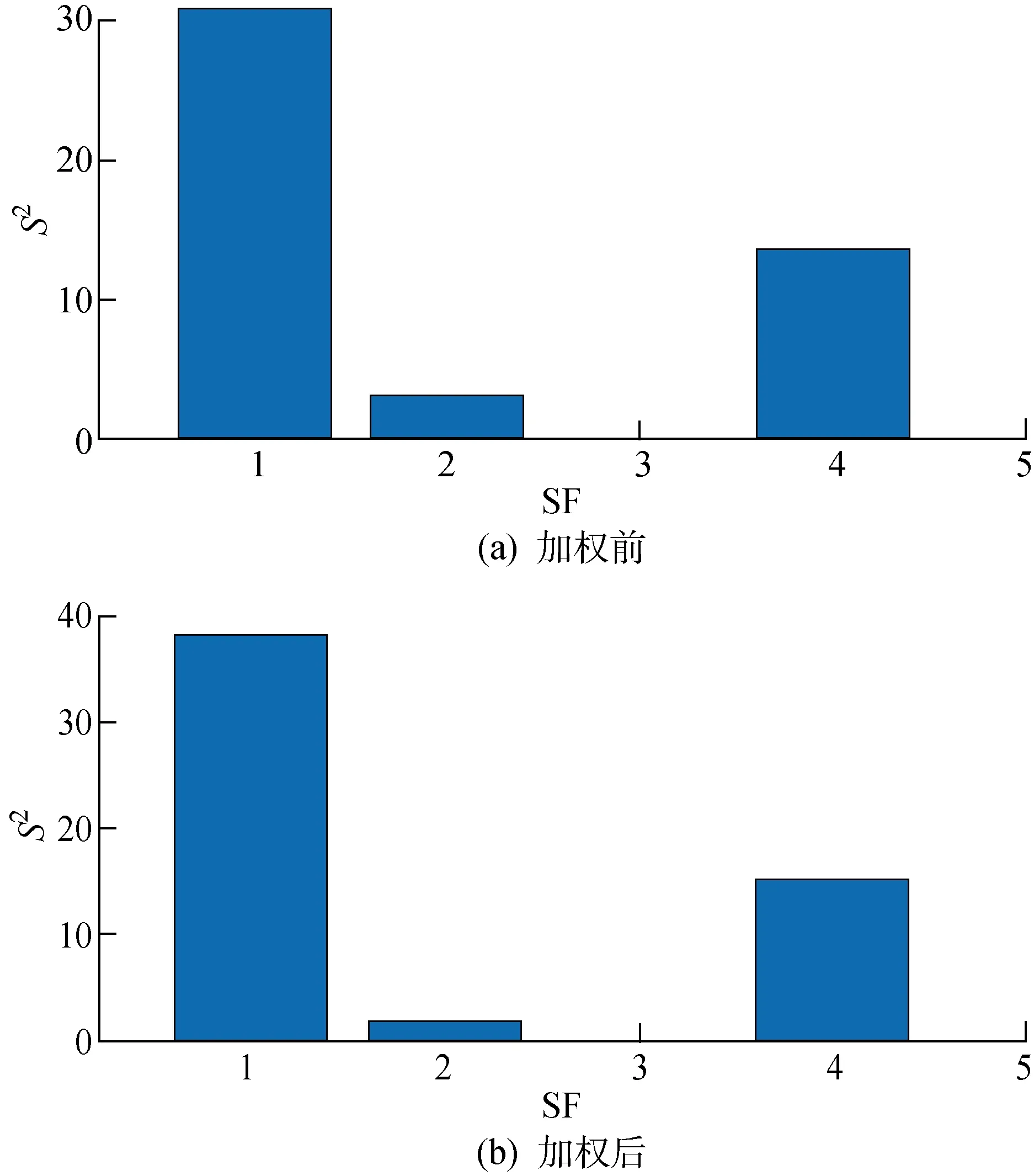
图2 各个嫌疑特征统计量

过程监测过程的松弛系数取0.8.PCA算法使用T2和SPE统计量，SFA算法以及OWSFA算法3种方法对不同故障的故障检测率如表1所示，其中最佳检测结果由粗体标出.故障1是h2处引入值为2的阶跃扰动，3种方法的监控结果如图3所示.由图3可知，OWSFA算法由于有着在线特征选择，挑选到了包含较多故障信息的部分数据特征，所以检测结果较好，整体检测率相比其余两种方法有着一定程度的提升.

图3 故障1监测结果

表1 3种方法的故障检测率

故障2是h1引入0.01(q-160)的斜坡扰动，3种方法的监测结果如图4所示.由于斜坡故障是随着时间推移逐渐变大的，其产生的初始时刻并不明显.由图4可知，PCA和SFA算法统计量最早在大约第350次采样处明显分辨出故障，而OWSFA算法能够在大约第300次取样处分辨出系统故障，有着一定的优势.由于斜坡故障在开始产生时并不十分明显，所以包含其故障信息的特征数据开始时不易被检测，OWSFA算法在进行特征选择时引入的阈值系数放宽了控制标准，将上述不易检测的故障信息也选择了进来，又通过权重赋值使故障信息突显.由此，OWSFA算法对此斜坡故障有着更高的检测率.

图4 故障2监测结果

3.2 Tennessee Eastman(TE)过程仿真分析

TE模型是由Downs等[21]提出，随后，Lyman 等[22]对TE 过程的控制系统进行了改进.TE过程有5个主要的单元操作：反应器、冷凝器、汽液分离器、循环压缩机和产品汽提器.TE过程共有33个过程变量.基准数据集包含500个样本，故障模拟器可以生成21种不同类型的故障.对于每个故障，前160个样本是正常数据，样本161～960是故障数据.故障检测过程的松弛系数取0.8.

对于故障1、2、4、6、12、13、14、18，3种方法都有着很好的检测率，基本都能达到95%以上.故障3、9、15用3种方法都较难检测出.相比于PCA算法和SFA算法，OWSFA算法对于故障10、11、20、21有较为明显的优势.OWSFA算法，由于结合了SFA算法的动态信息表达和在线加权的优势，能够检测出更多的故障.3种监测算法的检测率如表2所示，其中，对监控结果有着明显优势的部分进行了加粗处理.下面针对故障10和11进行详细分析.

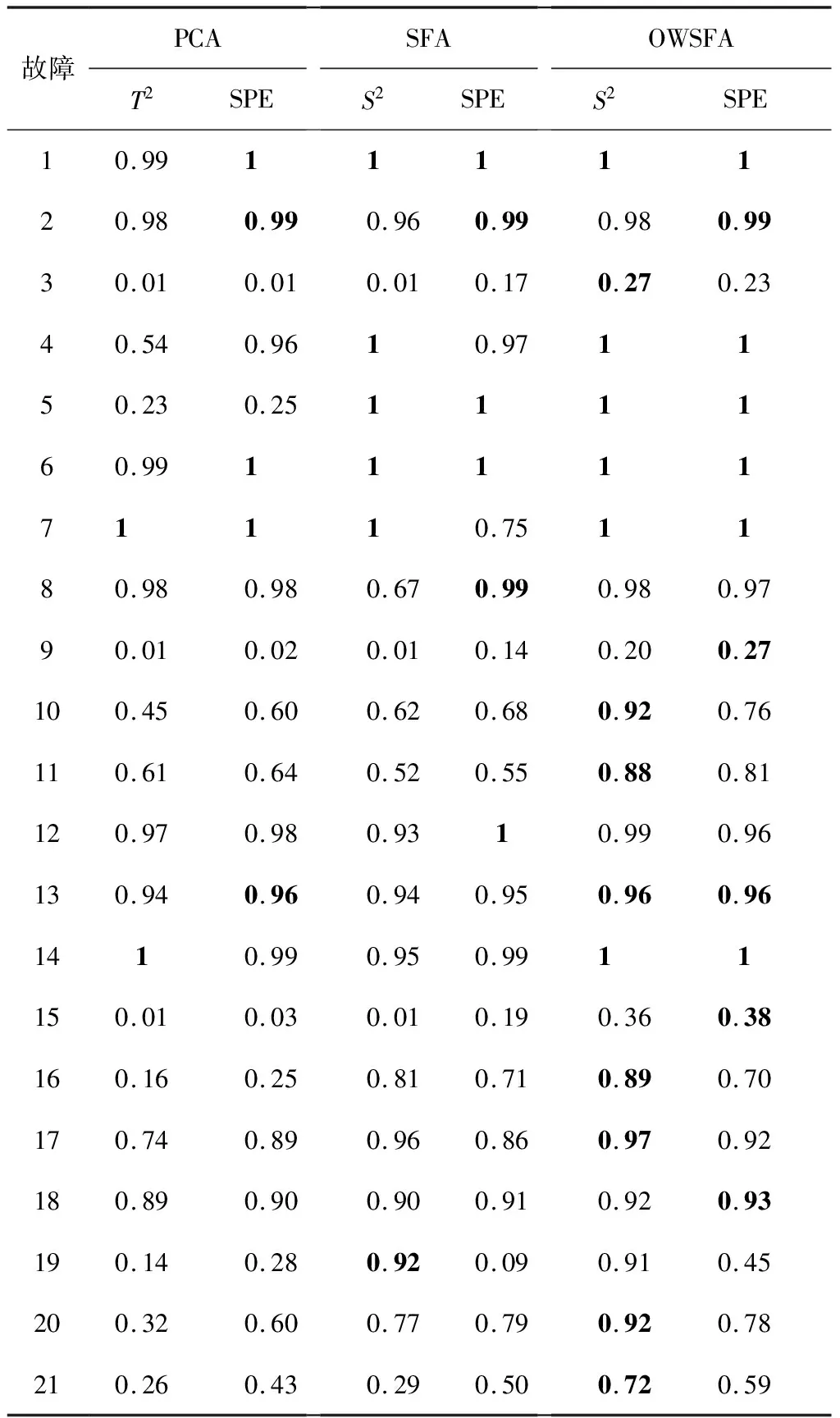
表2 TE过程故障检测率

故障10是C进料温度的随机变化.PCA，SFA，OWSFA算法的监测结果如图5所示.由图5可知，PCA算法的T2统计量检测率只有45%，检测效果不佳.SFA算法相比于PCA算法有着小幅度的优化.而OWSFA算法在原本SFA算法的基础上有了很大的进步，检测率可以达到92%.由于故障10属于随机变化故障，其故障值有时可能并不能明显体现，采用在线特征选择策略，引入权重系数计算统计量，能够突显故障信息，所以OWSFA算法可以显著地提高故障检测率.

图5 故障10监测结果

故障11是反应器冷却水入口温度的随机变化.PCA、SFA、OWSFA算法的监测结果如图6所示.由图6可知，PCA和SFA算法的检测率均低于70%，相比于PCA和SFA算法，OWSFA算法的S2统计量和SPE统计量检测率均有着一定程度的提高，故障检测率超过了80%.

图6 故障11监测结果

综上，SFA算法由于包含了动态信息，较传统的PCA算法有着一定程度的进步.OWSFA算法保留了原有SFA算法的监控优势，由于在线故障嫌疑特征选择和特征加权对故障检测有着极其重要的影响，使得故障检测模型更加有效，所以OWSFA算法有着更高的检测率.

4 结语

鉴于传统多元统计方法忽略了时变动态信息，无法为过程数据的动态行为提供明确的表示.此外，由于传统算法在进行特征选择时，没有利用在线故障信息，导致检测结果不佳.本文提出了一种基于在线加权SFA的故障检测方法，通过判断在线监测特征是否超过阈值来选择故障嫌疑变量，并且计算统计量时引入权重系数以凸显故障信息，实现了对过程系统的故障检测.利用慢特征分析算法提取过程系统的动态信息，在线嫌疑特征选择策略充分利用过程故障信息，引入松弛系数这一特征选择参数和权重系数这一统计量计算参数，很大程度上降低了选择在线特征时对阈值的依赖.根据TE过程仿真和数值系统仿真的结果，验证了本方法的可行性.