基于变步长梯形求积法的Volterra积分方程数值解

陈书坤，宁玉富

（山东青年政治学院 信息工程学院，山东 济南 250103）

通常，微分方程需要附加初值条件或边值条件，以形成定解条件；而积分方程本身已包含了初值或边值信息，导致积分方程的解法和微分方程的解法有较大的不同。特别是在求方程的数值解时，积分方程往往较微分方程更容易、更直接。

1 线性Volterra积分方程

随着计算机科学与技术的发展，积分方程的数值算法不断涌现[1-10]。本文主要考虑第二类线性Volterra积分方程，其一般形式为：

方程中，k(x,t)和g(x)为已知函数，f(·)为未知函数。

当被积函数没有给出表达式，或者被积函数有表达式但原函数不是初等函数时，就必须通过数值积分的办法将积分方程离散化，用所得到的方程去近似逼近原方程。在区间[a,b]上取若干节点，并将其分为N个小区间，式（1）中的积分项就可以用梯形求积公式来逼近。应用梯形求积公式求解线性Volterra积分方程，后面节点处的误差要比前面节点处的误差大。为减少最后节点处的误差，考虑使N个小区间的长度逐渐减小。本文提出了两种变步长方法，并将所提方法结合算例进行验证，与等步长相比，结果精度有一定的提高。

2 变步长的复化梯形求积法

2.1 复化梯形求积法

在区间[a,b]上取若干节点将其分为N个小区间，式（1）中的积分项就可以用梯形求积公式来逼近。假定方程（1）的解f(x)，g(x)，k(x,t)均为[a,b]区间的连续函数，并设节点为：

其中，hi(i=1,2,…,N)是步长，且：

将节点xi,i=0,1,2,…,N依次代入式（1），得：

式中，每个积分项用梯形求积公式可变为：

其中，fi=f(xi),gi=g(xi),kij=k(xi,xj)。

2.2 变步长策略

应用梯形求积公式求解线性Volterra积分方程，后面节点处的误差要比前面节点处的误差大。为减少最后节点处的误差，考虑使N个小区间的长度逐渐减小。为此，提出如下变步长策略。

变步长1：步长h1,h2,…,hN为等差递减数列，设公差为-d，即：hi－hi－1=d＞0，i=2,3,…,N，令最后步长为hN＝α，则：

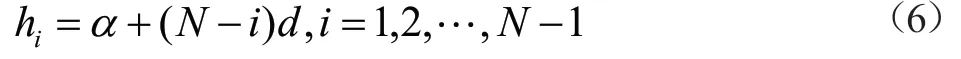
将式（6）代入式（3），得：

由式（7）得最后步长，可表示为：

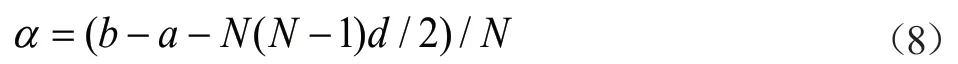
变步长2：步长h1,h2,…,hN为递减等比数列，设步长hi=ke-λi，其中，常数k,λ＞0。将hi代入式（3）得：

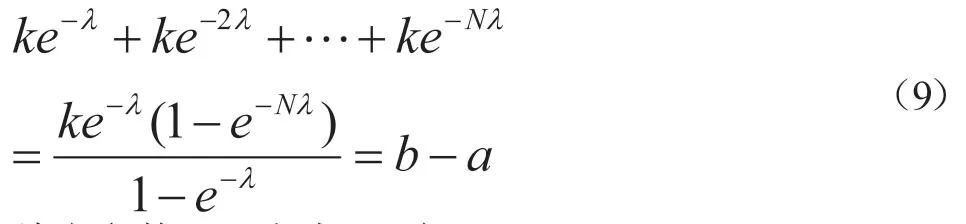
给定参数λ，可由式（9）得k：

3 数值实验

为了检验所提算法的有效性，针对算例进行数值实验。所有相关计算在PC机（2.4 GHz CPU，4 G内存）上用Matlab7.0编程实现。

用精确解和近似解间的绝对误差（Absolute Error，AE）评价所提算法的精度，定义如下：

其中，f(xi)为未知函数f(x)在xi的精确解，而(xi)为未知函数f(x)在xi处用所提方法得到的近似解。

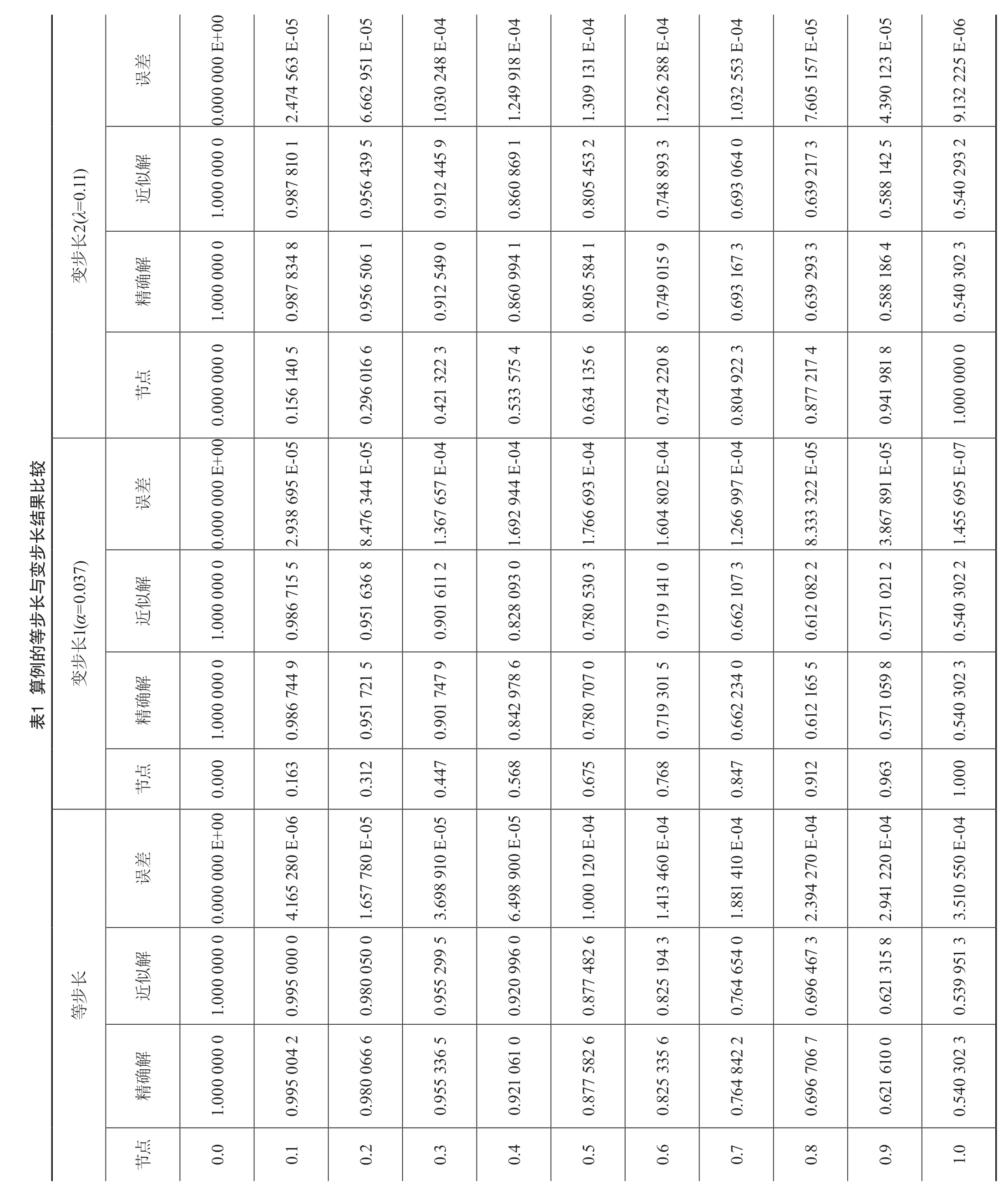
等步长和变步长的梯形求积法求解第二类线性Volterra积分方程的近似解，具体如表1所示。近似解的散点图和精确解的曲线如图1所示。由数值结果可知，所提变步长方法在后几个节点近似解精度明显优于等步长方法在后几个节点近似解精度，说明所提方法是可行的和有效的。

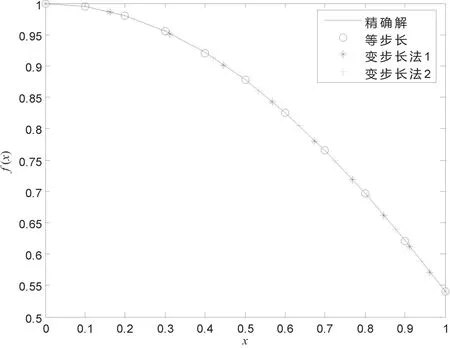
图1 算例近似解与精确解的图形

差误解近似2(λ=0.11)长精确解长1(α=0.037)变步节点长结果比较差误步长与变解步近似等表1 算例的步变确解精节点差误解长等步近似精确解1.000 000 0 1.000 000 0 0.000 000 E+00 0.000 1.000 000 0 1.000 000 0 0.000 000 E+00 0.000 000 0 1.000 000 0 1.000 000 0 0.000 000 E+00 0.995 004 2 0.995 000 0 4.165 280 E-06 0.163 0.986 744 9 0.986 715 5 2.938 695 E-05 0.156 140 5 0.987 834 8 0.987 810 1 2.474 563 E-05 0.980 066 6 0.980 050 0 1.657 780 E-05 0.312 0.951 721 5 0.951 636 8 8.476 344 E-05 0.296 016 6 0.956 506 1 0.956 439 5 6.662 951 E-05 0.955 336 5 0.955 299 5 3.698 910 E-05 0.447 0.901 747 9 0.901 611 2 1.367 657 E-04 0.421 322 3 0.912 549 0 0.912 445 9 1.030 248 E-04 0.921 061 0 0.920 996 0 6.498 900 E-05 0.568 0.842 978 6 0.828 093 0 1.692 944 E-04 0.533 575 4 0.860 994 1 0.860 869 1 1.249 918 E-04 0.877 582 6 0.877 482 6 1.000 120 E-04 0.675 0.780 707 0 0.780 530 3 1.766 693 E-04 0.634 135 6 0.805 584 1 0.805 453 2 1.309 131 E-04 0.825 335 6 0.825 194 3 1.413 460 E-04 0.768 0.719 301 5 0.719 141 0 1.604 802 E-04 0.724 220 8 0.749 015 9 0.748 893 3 1.226 288 E-04 0.764 842 2 0.764 654 0 1.881 410 E-04 0.847 0.662 234 0 0.662 107 3 1.266 997 E-04 0.804 922 3 0.693 167 3 0.693 064 0 1.032 553 E-04 0.696 706 7 0.696 467 3 2.394 270 E-04 0.912 0.612 165 5 0.612 082 2 8.333 322 E-05 0.877 217 4 0.639 293 3 0.639 217 3 7.605 157 E-05 0.621 610 0 0.621 315 8 2.941 220 E-04 0.963 0.571 059 8 0.571 021 2 3.867 891 E-05 0.941 981 8 0.588 186 4 0.588 142 5 4.390 123 E-05 0.540 302 3 0.539 951 3 3.510 550 E-04 1.000 0.540 302 3 0.540 302 2 1.455 695 E-07 1.000 000 0 0.540 302 3 0.540 293 2 9.132 225 E-06节点0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0

4 结语

针对变步长梯形求积公式求解线性Volterra积分方程时，后面节点处的误差要比前面节点处的误差大的缺点，本文提出了两种变步长逐渐减小的方法。数值实验验证了所提变步长方法在后几个节点近似解精度明显优于等步长方法在后几个节点近似解精度，整体精度有提高，说明所提方法是可行的和有效的。