柔性变形下车窗升降三维装配公差建模及优化
2020-12-15王国亮朱文峰
钱 鹏, 王国亮, 朱文峰
(1.同济大学 机械与能源工程学院,上海 201804; 2.中国航发商用航空发动机有限责任公司,上海 200241)
公差设计是决定产品质量的重要因素之一,偏差分析是产品尺寸工程的核心部分.传统公差分析有极值法、统计法和蒙特卡洛法等[1].随着计算机技术的发展,计算机辅助公差设计逐渐成为主流.目前常用的三维公差仿真分析软件大多基于刚性假设,对刚度较小、柔性较大的车身薄板柔性件不再适用[2].
国内外学者对柔性体的公差分析理论方法进行了研究.穆晓凯等[3]通过最小二乘法、小位移旋量理论以及齐次坐标变换理论建立了考虑外载荷的三维装配偏差分析的数学模型;Hashemian 等[4]通过有限元法计算柔性件在装配、装夹过程中产生的变形对装配偏差的影响;Jayaprakash 等[5]运用有限元法计算惯性和温度产生的变形对电机装配的影响,通过优化公差减少了12.77%制造成本.
针对车身柔性件刚度小、易变形的结构特性,本文基于车身柔性件装配偏差分析理论,考虑到三维公差分析软件基于刚性假设的局限性,通过有限元仿真分析计算出Vis VSA无法考虑的机械变形、热变形等偏差源,形成一套较为完整的虚拟开发、验证以及优化的公差设计方法.为保证柔性件装配尺寸精度,考虑外部载荷对薄板件结构变形的影响,本文提出一种基于有限元变形数模重建的三维偏差建模分析方法,保证柔性件在受外部载荷存在变形偏差时装配体也能满足设计要求.
1 考虑车门内板柔性变形的玻璃升降器三维装配偏差分析
本文以绳轮式单导轨电动玻璃升降器为研究对象,针对车窗玻璃在升降过程中出现的抖动、卡滞以及车门内板刚度不足等不平顺问题,采用有限元与三维公差设计相结合方法,考虑升降载荷对车窗玻璃与密封条装配关系的影响,建立包含有限元变形的三维装配公差分析模型[6],揭示了密封阻力、车门内板的刚度对升降器装配状态的影响,通过优化公差设计提升玻璃升降系统的升降平顺性,具体实施方法如图1所示.

图1 基于有限元法的玻璃升降器三维装配公差分析流程
1.1 基于Adams的电动玻璃升降器动力学建模
在玻璃上升过程中,升降器必须克服自身的重力,该过程中受到的阻力是最大的.因此,本文选取上升过程为例建立单导轨玻璃升降系统力学模型.
(1)模型预处理.本文使用多体动力学仿真软件(MSC.Adams 2017)进行动力学仿真运算,其中集成有绳索(cable)模块,可以快速对钢丝绳、导向轮等建模,因此在三维建模软件(CATIA)中将升降器总成进行简化时,只需保留玻璃、导轨、托架(滑块)等主体零件.
在模型导入之后,分别赋予构件材料属性,根据实际运动抽象出构件之间相应的运动副,从而模拟升降器的真实运动情况.整个系统的约束情况如下:导轨与大地、玻璃与托架、托架与卡扣之间添加固定副;滑块总成与导轨之间添加接触与滑动副.
(2)驱动及传动建模.依据升降器相关技术资料获取卷丝筒、上下导向轮的几何属性和安装位置坐标,采用Adams软件集成的cable建立钢丝绳传动模型[7].
本文采用玻璃升降器的实测运动状态作为驱动输入,以Adams/Cable模块中的绞盘(Winch)功能模拟钢丝绳收放功能,实现玻璃的升降运动.如图2所示:分别在与滑块相连的两个螺栓上建立2个无质量属性的锚固点1-1和2-1为连接两段钢丝绳的起点,在卷丝筒外侧分别建立2个无质量属性的锚固点1-2和2-2作为两段钢丝绳的终点,完成钢丝绳的建模.为实现升降器的运动,分别在点1-2和2-2处添加Winch,以上升工况为例,钢丝绳1处于收缩状态,钢丝绳2处于释放状态,其收缩、释放的长度相等,则有
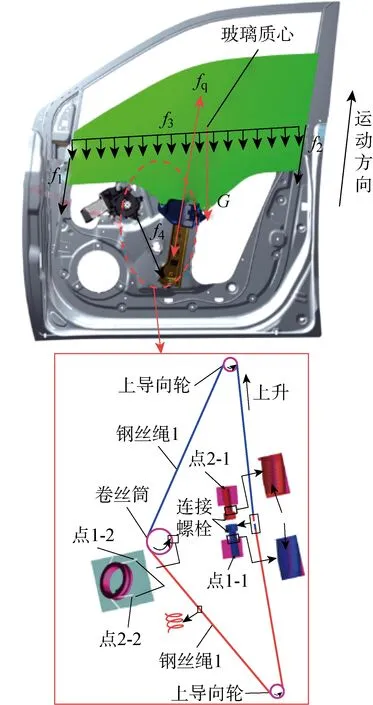
图2 升降器受力分析及钢丝绳建模
W1=W2
(1)
式中:W1为上绞盘收缩的钢丝绳长度;W2为下绞盘释放的钢丝绳长度.
(3)添加外载荷.车门玻璃在上升运动中,除自身的重力G外,还受到车窗前、后导槽密封条的阻力f1和f2、内外水切条摩擦阻力f3、卡扣与导轨的摩擦力f4以及升降器的运动牵引力Fq.
前后导槽密封阻力根据下式计算得到:
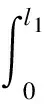
(2)

(3)
式中:μ为密封条摩擦系数;l1、l2分别为玻璃与前后导槽接触长度;Nin、Nout分别为内外唇边对玻璃的压缩负荷.车门密封条材料参数如表1所示.

表1 车门密封条材料参数
水切密封阻力如式(2),在Adams中借助IF条件判断函数式和DZ方向位移函数表示该方程[8]:
(4)
式中:h为玻璃升程.
(4)仿真分析结果.将设置好的模型初始化:以驱动速度为110 mm/s,参考玻璃实际升程所用时间,设置仿真时间为3.5 s,迭代步长0.01 s,运行仿真运算.
输出钢丝绳的受力曲线如图3所示:升降器刚启动时,钢丝绳1受力迅速增大,达到103.7 N,此过程也为玻璃加速阶段;随着玻璃达到设定运行速度,停止加速后钢丝绳拉力也趋于平稳,恒定在75 N,当玻璃到达最高位置时,电机堵转,产生较大的堵转力,达到了143.7 N.钢丝绳作为一种软连接,故钢丝绳2对于玻璃上升运动无明显力学作用,只受初始预紧力10 N.该过程与车窗关闭过程相符合.

图3 玻璃升降器动力学仿真结果
1.2 基于ANSYS的车门内板变形计算
车门有限元模型主要是车门内板的钣金件,忽略了车门内饰板、车门外板等部件,简化了车门把手、车门铰链以及门锁等结构,以简化的约束代替.
(1)几何特性.本文中模型料厚为0.8 mm,弹性模量为210 GPa,密度为7.8 t/m3,泊松比为0.3.为保证计算效率,除升降器安装孔外,车门内板上小于5 mm的圆角、倒角以及半径小于10 mm的圆孔等细节特征均被忽略.
(2)网格划分.本文按照白车身网格划分的标准,采用模型主要采用shell单元进行划分,网格尺寸控制在5~10 mm,以四边形单元为主导,在一些过渡的区域采用三角形单元加以辅助.
(3)边界条件.根据车门内板模态试验、升降器安装面刚度试验条件,模拟出如下约束条件:① 约束铰链安装孔该点的5个方向的自由度,释放绕Y轴方向的旋转自由度模拟车门与白车身的连接、铰链旋转;② 约束门锁的安装点3个平动自由度,模拟门锁止时的状态.
车门内板所受到的外界载荷主要有自身重力以及升降器安装面受到的升降载荷.升降载荷的加载为:沿玻璃升降器安装孔的法向建立局部坐标系,并在上安装面局部坐标系XOY平面内施加150 N的载荷,下安装面局部坐标系XOY平面内施加20 N的载荷.车门内板有限元分析模型如图4所示.

图4 车门内板有限元分析模型
(4)仿真分析结果.车门内板的位移分布如图5所示:车门内板升降器上安装面在升降载荷作用下产生了0.594 mm的变形量,下安装面的变形量为0.393 mm.

图5 车门内板变形
1.3 基于Vis VSA玻璃升降器三维公差分析
影响升降器装配偏差的因素较多,本文仅选取车门内板、玻璃、升降导轨以及托架(托架-卡扣分总成)等对玻璃升降器装配偏差影响较大的零部件作为分析对象.
(1)尺寸目标.玻璃导槽密封胶条安装在窗框导轨上,在车窗玻璃升降过程中与玻璃接触,直接影响到玻璃升降的运行状态.
为确保车窗玻璃密封性能,避免玻璃升降阻力过大,选取导槽密封条与玻璃压缩量a以及内外水切与玻璃压缩量b作为尺寸目标,作为量化升降平顺性优化的评定参数.结合密封系统的性能以及材料要求,确定玻璃与密封条配合关系如图6所示[9].

图6 玻璃与密封条装配状态
(2)定义初始公差.本文对玻璃升降系统相关零部件的基准和公差定义采用ASME标准,公差值的设定采用冲压件通用公差要求,如图7~10所示.
(3)建立测量.分别在玻璃前后边缘以及水切处建立如图11所示11个测点以模拟玻璃升降过程中所处的不同位置,f、b、s分别表示玻璃前缘、后缘及水切处的测点.
(4)理想状态装配公差分析结果.依据各零部件的公差定义相关特征、基准,依据图7中的虚拟装配关系添加约束条件,即定义各个零部件之间的装配面进行贴合、孔和销的配合操作等,建立各测点的测量关系.

图7 车门内板公差设定
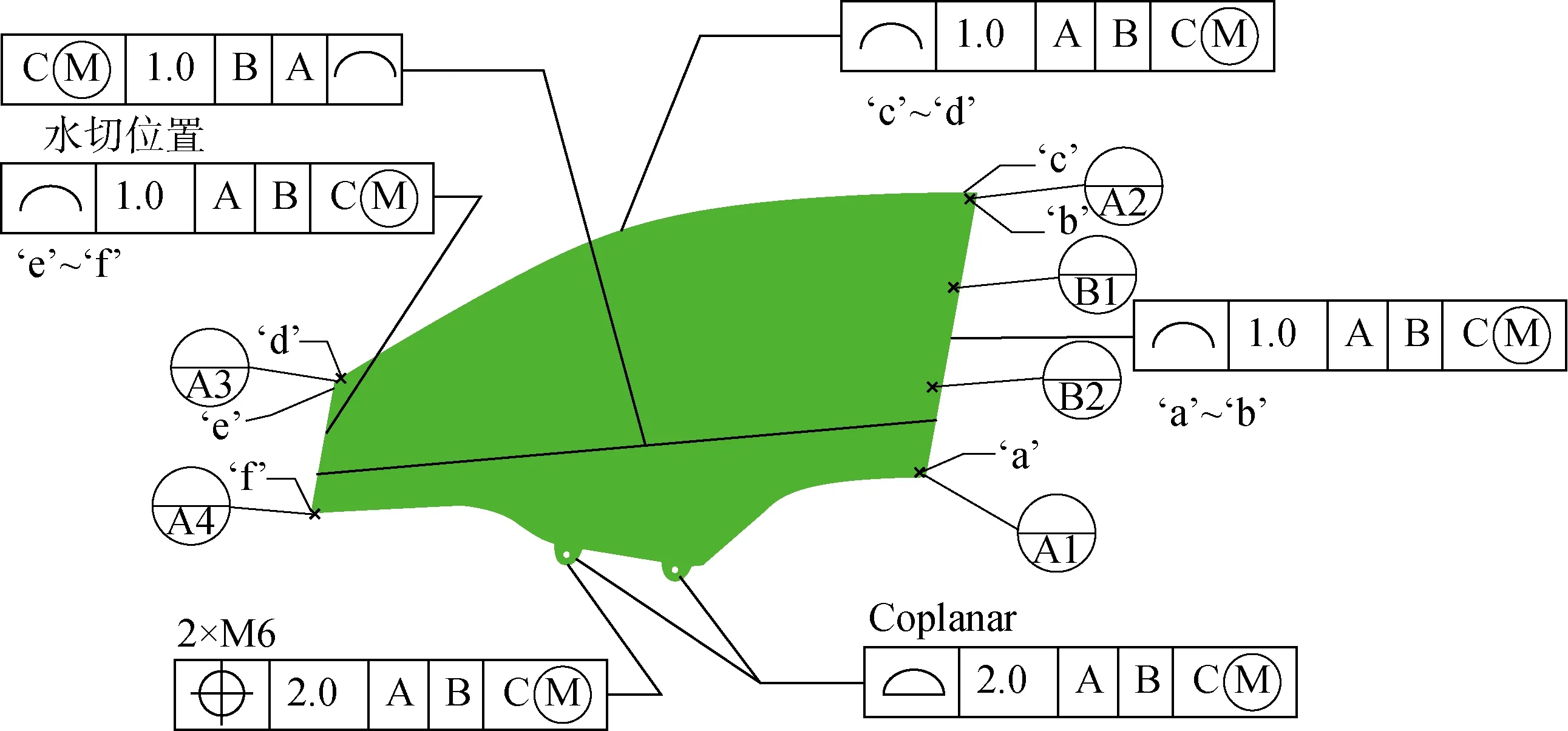
图8 车窗玻璃公差设定

图9 托架总成公差设定

图10 导轨公差设定

图11 车窗玻璃测点分布
设定迭代计算次数为 5 000 次,运行蒙特卡洛仿真,公差验证范围为6σ(±3σ),各测点迭代计算的结果见表2.

表2 理想状态下装配偏差计算结果
在玻璃前后边缘设置的测点对密封条压缩量偏差分布值从下至上缓慢增加.就整体偏差来看,后边缘对密封条的压缩量偏差值最大,为 2.159 3 mm,发生在玻璃上升到顶端导槽的入槽位置,符合公差传递的过程;水切部位的压缩量波动较平稳,偏差最大值为 1.450 2 mm;均在设定的尺寸目标范围内,能够满足升降平顺性的要求.
(5)考虑车门内板柔性变形的装配偏差分析.根据有限元分析计算结果,结合尺寸模型中用于导轨与车门内板装配点坐标,分别提取有限元节点的X、Y、Z三个方向的变形量,在Vis VSA重新建立车门内板与导轨的匹配点,见表3.

表3 车门内板安装面坐标变化
将变形后的安装面节点坐标重构,保留初始GD&T图纸标注要求,建立相关基准特征、装配特征以及测量特征.基于特征建立基准、装配关系以及测量方案,运行迭代计算,验证在升降载荷作用下的装配偏差能否满足尺寸目标要求,计算结果见表4.

表4 升降载荷下装配偏差计算结果
在考虑车门内板的导轨安装面变形时,随着玻璃的上升运动,玻璃与前后导槽密封条的压缩量超差率逐渐增加.装配关系最差点出现在玻璃入槽阶段后边缘上顶点,超差率为6.0%;水切密封的装配关系所受影响不大,仅靠近玻璃后边缘的测点存在0.67%的超差率.
因此,虽然在理想状态下的玻璃各测点的偏差分布都在尺寸目标要求内,满足升降平顺性要求,但在升降载荷及自身重力作用下,车门内板的导轨安装面产生的变形偏差通过导轨、托架传递到玻璃上产生了装配偏差,导致玻璃前后边缘对密封条的压缩量增大,之前设定的尺寸要求不再满足尺寸目标要求,无法保证升降过程的平顺性.故需要对现有的公差设定进行优化设计,以达到稳健设计要求.
2 基于实验设计的公差方案优化
在考虑升降载荷作用下,超差率最大的点是玻璃后边缘的顶点,本文优先控制该点的偏差,确定优化方案,进而校核其他测点的偏差分布能否满足设定的尺寸目标.依据蒙特卡洛迭代计算报告建立偏差传递的模型,基于主成分分析,采用降维思想,提取较为关键的影响因子作为设计变量进行实验设计,提高优化效率.
(1)提取设计变量.依据迭代计算结果,将该测点的影响因素报告汇总,见表5.

表5 装配偏差因素
排名靠前的两个影响因素为导轨-托架的配合特征,故而将其作为一个整体考虑,本文选取导轨和托架的配合面的面轮廓度、玻璃和托架的安装孔的位置度为设计变量.
(2)实验设计优化.采用实验设计的方法,结合公差设计常用尺寸,通过控制变量法,选取单个变量的公差值为唯一变量,进行蒙特卡洛迭代计算得出各影响因素的公差变化对玻璃测点偏差波动范围的影响.
设定导轨-托架配合面轮廓度的公差带取值范围为0.4~1.0 mm,玻璃托架的安装孔位置度的公差取值范围为0.5~2.0 mm,分别在三维装配公差计算模型中修改两个参数的公差值设定,进行蒙特卡洛仿真计算,获取测点的偏差波动范围.公差值变化对测点偏差超差率的影响如图12所示.
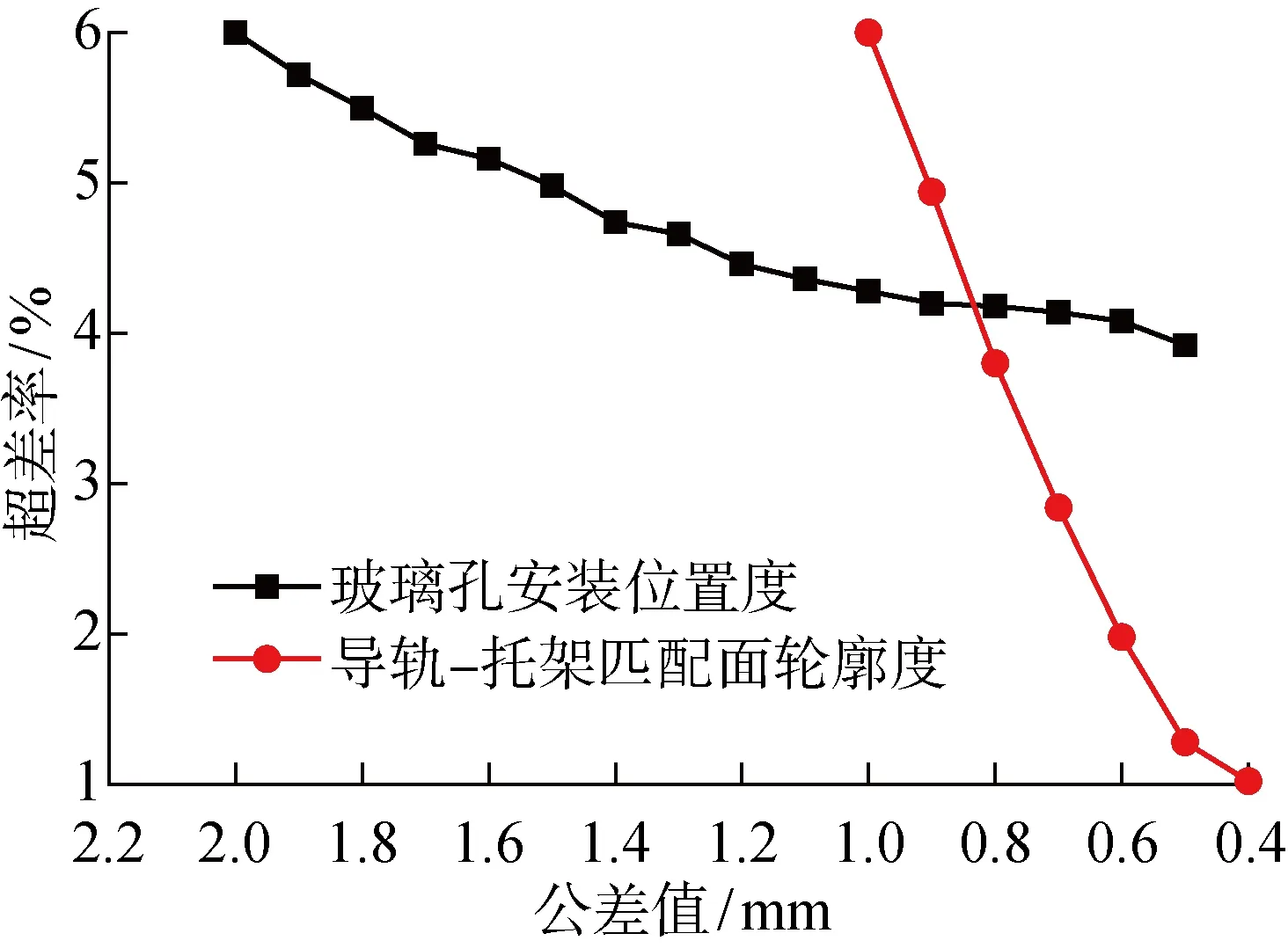
图12 公差值变化对测点超差率影响
由此可见,随着变量公差的设定值逐步递减,相应测点偏差的超差率也会逐渐减小,定义第i组形位公差值为Ti时,计算的超差率为Si,记每一组公差收严所带来的超差率减小的幅度为收益比ηi:
(5)
收益比的大小可以用图示折线段斜率表示,当面轮廓度公差小于0.5 mm时,收益比迅速下降,代表当轮廓度公差取值为0.4 mm时,其影响因子排名被改变,说明在继续加严轮廓度收效不会很明显,此时可以从其他影响因素着手进行控制;玻璃安装孔的位置度公差从2.0 mm逐步收严到0.5 mm过程中,存在两个收益比跳跃点,即位置度分别为1.4 mm与0.9 mm.故而本文优先选取(0.5-1.4)方案(轮廓度为0.5 mm、位置度为1.4 mm)和(0.5-0.9)方案(轮廓度为0.5 mm、位置度为0.9 mm)两种组合方案进行验证.
(3)公差优化方案验证.以考虑变形的三维装配公差分析模型为基础,分别设置两种不同的公差组合,计算结果分别如图13和14所示.

图13 (0.5-1.4)方案计算结果
(0.5-1.4)公差组合方案下,玻璃后边缘顶端测点的偏差分布范围为(0.661 3±1.566 7)mm,存在0.74%的超差率,该方案不符合3σ稳健设计准则.(0.5-0.9)公差组合方案下,玻璃后边缘顶端测点的偏差分布范围为(0.661 3±1.432 4)mm,存在0.12%的超差率,方案符合3σ稳健设计准则.(0.5-0.9)公差组合方案下,再次运行仿真迭代计算,对其他测点进行验证,验证结果见表6,迭代计算盒状偏差图如图15.
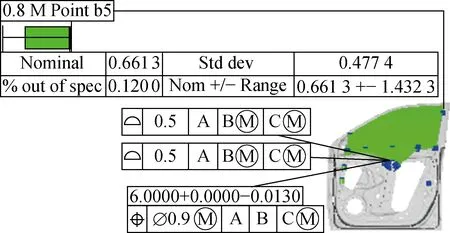
图14 (0.5-0.9)方案计算结果

图15 偏差波动盒状图
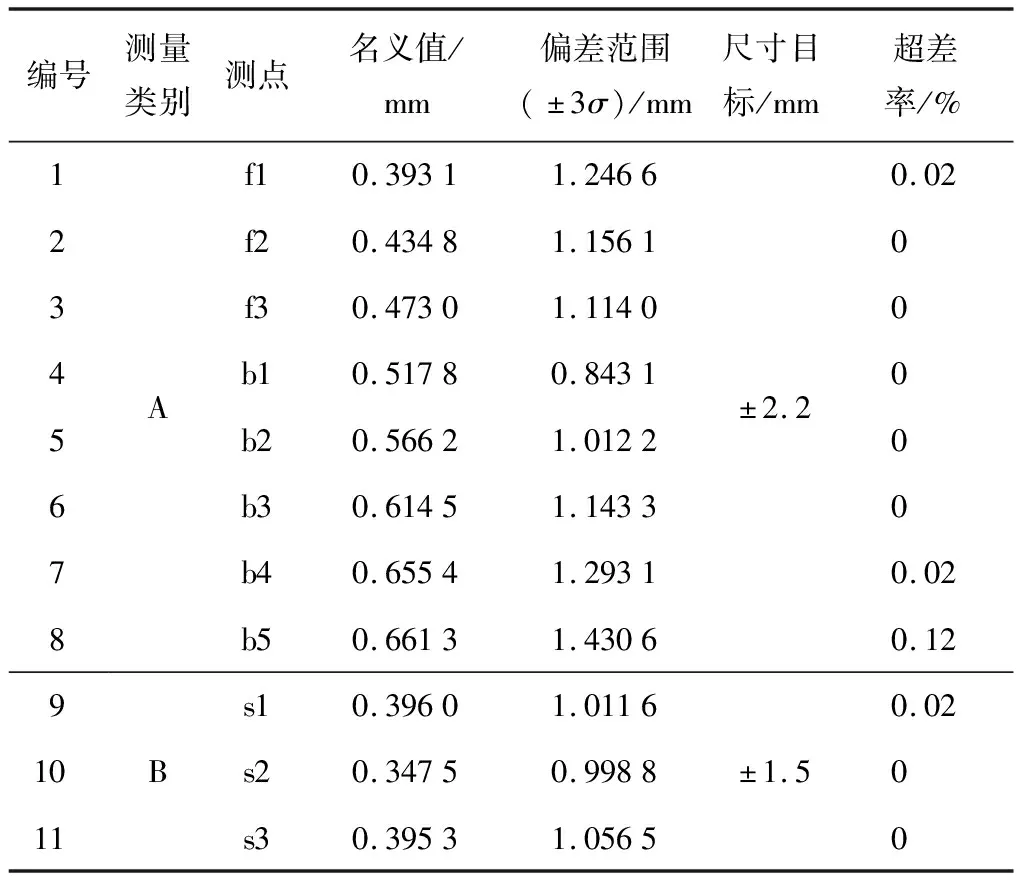
表6 偏差波动分析结果
由表6和图15可知:将导轨-托架匹配面的面轮廓度收严到0.5 mm,玻璃-托架安装孔位置度收严到0.9 mm之后,考虑在升降载荷作用下的车门内板柔性变形的三维装配公差分析模型所有测点均符合设定的尺寸目标要求,能够满足升降平顺性要求.
3 结论
(1)针对车门柔性件变形会影响车窗升降系统装配偏差计算的问题,结合玻璃升降器动力学、静力学以及三维公差设计方法,开发出一套面向升降平顺性的虚拟开发、验证以及优化的公差设计方法.
(2)本文以某车窗升降系统的三维装配公差分析为例,以公差收严的收益比为评价因素,实现了考虑车门内板变形的升降器公差组合方案优化设计,结果表明在导轨-托架匹配面的面轮廓度为0.5 mm,玻璃-托架安装孔位置度为0.9 mm的情况下,车门模型的装配公差符合设定目标,满足升降平顺性要求.
