基于频率法的短吊杆索力测试

2020-11-19燕启清刘世忠朱占龙李登科

铁道科学与工程学报 2020年10期

燕启清，刘世忠，朱占龙，李登科

基于频率法的短吊杆索力测试

燕启清1，刘世忠1，朱占龙2，李登科2

(1. 兰州交通大学土木工程学院，甘肃兰州 730070；2. 中铁西北科学研究院有限公司，甘肃兰州 730000)

为提高基于频率法的短吊杆索力测试精度，结合现有文献中吊杆索力与其自振频率之间的显式关系式，通过对影响吊杆索力测试精度的因素进行分析，引入边界条件修正系数修正吊杆两端复杂边界条件；在频率法测试吊杆拉力计算公式的基础上，引入吊杆索力偏差系数用于短吊杆的界定；提出一种考虑短吊杆抗弯刚度、复杂边界条件的索力比例系数标定方法及索力计算公式。将其运用在某64 m下承式钢管混凝土系杆拱桥施工监控中，算例表明：相对于传统索力测试计算方法，使用该方法使短吊杆索力测试精度提高了13.4%，且吊杆有效长度越短，精度提高得越多。

频率法；短吊杆索力测试；边界条件；抗弯刚度；吊杆索力比例系数标定

吊杆索力测试的方法主要有压力表法、压力传感器法、频率法、振动波法、三弯点法、磁通量法及其他方法等。频率法作为一种操作简单、经济便利的间接测试方法仍具有一定的实用价值。关于基于频率法的拉索索力测试方法及计算公式，国内许多专家学者做了大量的研究。史杰等[1]提出了吊杆有效长度的标定方法；薛刚等[2]进行了基于频率法测试吊杆索力的室内实验；于孟生等[3]分析了吊杆有效长度对索力测试的影响；何雄君等[4]研究了拉索有效长度、HDPE套管对拉索索力测试的影响；李晓章[5]对多阶频率法、2种附加质量法、基于频率法的吊杆索力测试方法进行了比较；刘承斌等[6]就拉索垂度对其索力测试计算的影响进行了室内实验。此外，Kangas等[7−9]对吊杆索力与其自振频率之间的关系做了大量的研究并将其运用到工程实践中，同时MA等[10−12]提出了基于频率法的吊杆索力灵敏度修正识别系统，并通过与有限元分析结果相互验证证明其可靠性。本文结合现有文献中吊杆索力与其自振频率之间关系的表述，提出一种考虑吊杆两端边界条件、横向抗弯刚度的短吊杆索力测试方法，并对短吊杆做出界定，将此方法运用在某下承式钢管混凝土系杆拱桥中取得了良好的测试效果。

1 普遍采用的吊杆索力监测方法

在施工监控过程中通常采集各吊杆的自振频率，结合前期标定的吊杆索力比例系数计算各吊杆索力值，并与设计值做对比，以此作为是否进行调索的依据。不考虑吊杆横向抗弯刚度对吊杆索力测试的影响时，吊杆索力比例系数标定公式及索力计算公式是以弦振动理论为基础的。根据弦振动理论，吊杆索力与其自振频率之间的显式关系式为[13]：

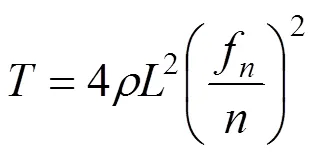
式中：为吊杆的线密度；为吊杆有效长度；f为吊杆第阶自振频率；为吊杆索力；为吊杆自振频率阶数。

令42，f=f/n，则有

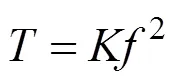
假设某吊杆在张拉完成之后其他吊杆张拉之前的时间段内该吊杆的索力是不变的，则此时该吊杆的索力Q可通过吊杆锚固时千斤顶油表读数带入千斤顶标定方程换算得到。当采用吊杆1阶自振频率计算吊杆索力时，吊杆索力比例系数的标定公式为：

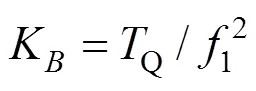
式中：Q为由千斤顶油表读数得到的吊杆索力，即标定阶段千斤顶张拉力；1为吊杆张拉完成后用索力动测仪采集到的吊杆1阶自振频率(为消除张拉设备对吊杆自振频率采集的影响，应在吊杆张拉完成，张拉设备拆除后，其他吊杆张拉之前采集吊杆1阶自振频率)；K为标定的吊杆索力比例系数。不考虑吊杆横向抗弯刚度对吊杆索力测试的影响时，吊杆索力计算公式为：

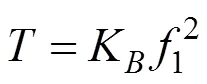
吊杆张拉完成后，采集各吊杆1阶自振频率并将其代入式(4)计算该阶段各吊杆索力值，以此作为第1次调索的依据。在拆除系梁支架及桥面铺装完成后，利用索力动测仪采集各吊杆1阶自振频率，用同样的方法可得到全桥吊杆索力，当实测索力与设计值之间的偏差超过规范要求时，须进行2次调索。

2 影响短吊杆索力测试精度的因素

2.1 吊杆横向抗弯刚度及边界条件

当吊杆两端边界条件可以假定为铰接时，吊杆索力与其1阶自振频率之间的显示关系式为[14]：

令=42，=1则有

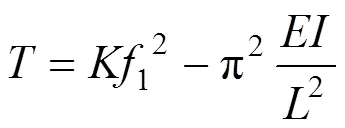
式中：为吊杆的拉压弹性模量；为吊杆的横向抗弯惯性矩，其余符号含义同上。

利用能量法，分别引入拉索横向振动在一端固接一端铰接、两端固接边界条件下的振型函数，得到的拉索索力与其1阶自振频率之间关系的表达式为[15]：

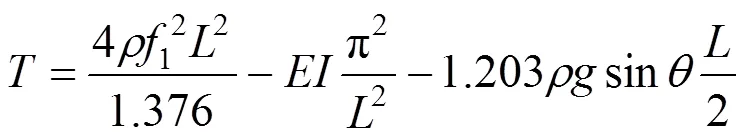
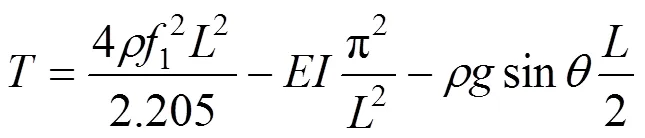
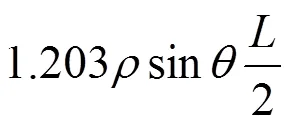
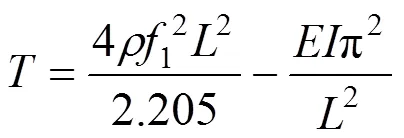
令=42，则吊杆索力计算公式可表示为：

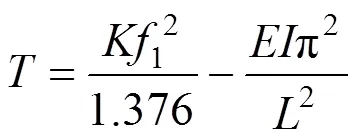
式中各符号的含义同上。

由式(2)和式(6)可以看出：吊杆横向抗弯刚度对吊杆索力计算值的影响为π2/2，与吊杆有效长度的平方成反比。由式(6)和式(10)可以看出，若不考虑吊杆横向抗弯刚度，边界条件拟定为铰接时计算得到的吊杆索力是拟定为一端铰接一端固接、两端固接时的1.376倍和2.205倍。吊杆的边界条件并非单纯的铰接或固接，而是介于两者之间，引入边界条件修正系数λ，假设由吊杆索力的变化引起的吊杆有效长度、拉压弹性模量、抗弯惯性矩、线密度的改变可忽略不计，根据式(6)和式(10)可以得到考虑吊杆复杂边界条件和吊杆横向抗弯刚度的索力计算公式：

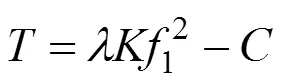
式中：为吊杆边界条件修正系数；为吊杆横向抗弯刚度修正值，对于单根吊杆其表达式为：

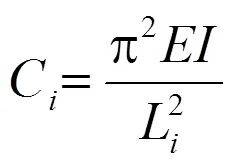
式中：为吊杆编号。基于假定，C为常数，故在吊杆第1次张拉阶段仅标定即可，的标定公式为：

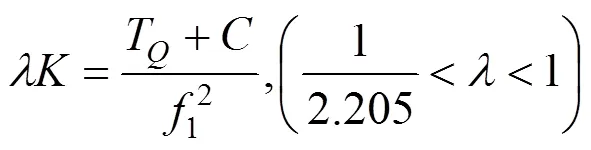
式中：T为标定吊杆索力比例系数时的千斤顶张拉力，其余符号含义同上。工程实践中，若吊杆分2个阶段张拉至设计索力，一般在吊杆第1次张拉阶段标定，在吊张第2次拉阶段对进行复核。

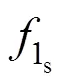
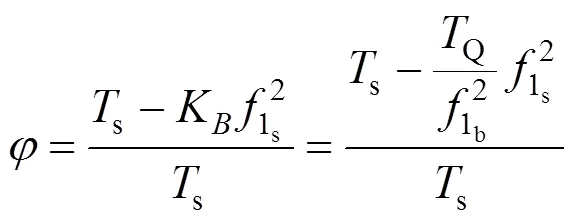
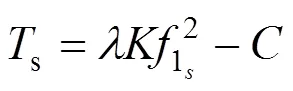
比例系数标定阶段(吊杆第1次张拉阶段)吊杆张拉力设计值b与张拉吊杆时的千斤顶张拉力Q相近(两者相近程度与千斤顶油表读数精度相关)，则：

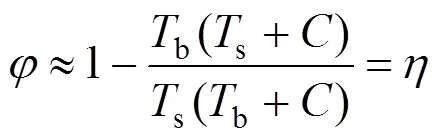
2.2 吊杆有效长度

关于吊杆有效长度的确定，工程实践中最常用的几种方法均是在吊杆与拱肋、系梁的连接方式为墩头锚的情况下提出来的。现有文献中提出的2种吊杆有效长度计算公式分别为[16]：

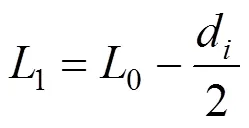
式中：1和2为吊杆有效长度；0为吊杆总长，即吊杆上、下锚固端之间的距离；d为吊杆锚固区总长。

目前系杆拱桥吊杆与系梁、拱肋的连接大多采用锚箱和冷铸锚，采用此种连接方式时，吊杆锚固区长相对于吊杆总长是很小的。在吊杆索力与其自振频率关系的表达式中，吊杆有效长度均是以平方的形式出现的。显然，当吊杆与拱肋、系梁的连接方式采用锚箱和冷铸锚时，吊杆有效长度的确定对吊杆索力监测精度的影响要比采用墩头锚时小得多。

3 算例

3.1 工程概况

某下承式钢管混凝土简支系杆拱桥平面位于=800 m的圆曲线上，系梁全长66.5 m，计算跨径64.0 m。系梁采用单箱双室预应力混凝土箱形截面，梁高1.9 m。拱肋横断面采用哑铃形钢管混凝土等截面，拱轴线采用二次抛物线，拱肋之间设2道一字撑和2道k撑，钢管横撑内均不内填混凝土。吊杆采用PES(FD)7-85平行镀锌高强钢丝，布置形式为平行布置，布置间距为5 m，全桥共设9对吊杆，共计18根。该桥采用先梁后拱的施工方法，先在支架上浇筑系梁、张拉预应力束，然后在系梁上搭设拱肋支架、拼装焊接拱肋、压注拱肋混凝土。待拱肋混凝土强度达到设计要求之后安装吊杆，按设计张拉顺序、张拉力分阶段张拉吊杆。吊杆张拉完成之后，测试、计算全桥吊杆索力，当计算值与该施工阶段吊杆索力设计值之间的差值在±5%以内时，拆除拱肋、系梁支架，进行二期施工。

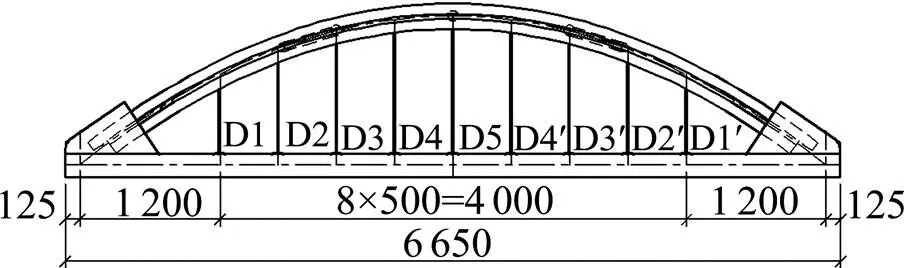
单位：cm

3.2 吊杆张拉顺序及张拉力

吊杆分2个阶段张拉至设计索力，4根相互对称的吊杆同时张拉且张拉力一致，2个张拉阶段吊杆设计张拉力设计值(张拉目标值)及张拉顺序如表1所示，表中1i表示吊杆第2次张拉阶段各吊杆张拉力设计值，表中2i表示吊杆第2次张拉阶段各吊杆张拉力设计值。吊杆张拉完成后各阶段吊杆索力设计值如表2所示。

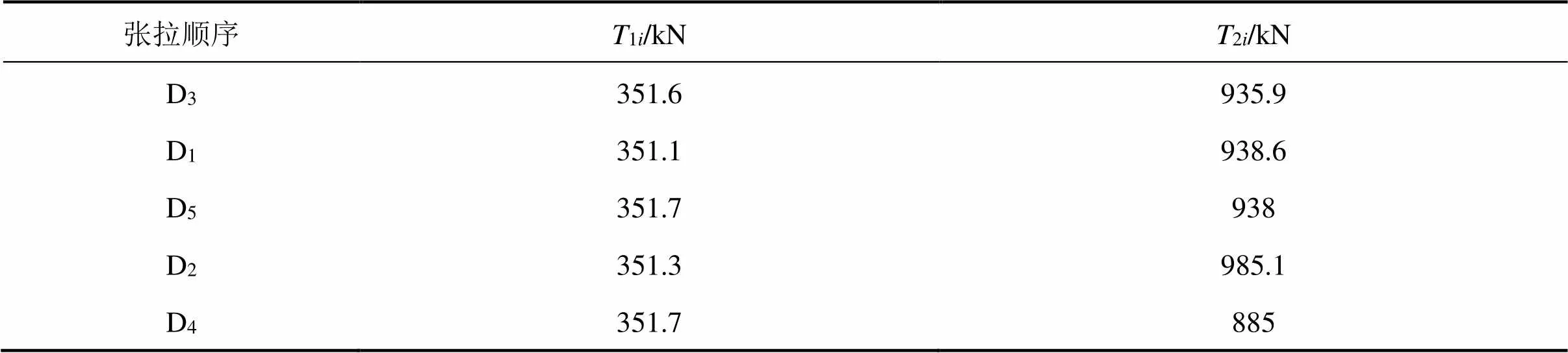
表1 吊杆张拉力设计值及张拉顺序

吊杆第2次张拉阶段是指在吊杆第1次张拉完成的基础上，按吊杆第2次张拉阶段的张拉设计值进一步张拉吊杆，2个张拉阶段的区别仅在于吊杆第2次张拉阶段吊杆索力发生了改变，但桥梁其他状态未发生变化，故可采用吊杆第2次张拉阶段吊杆实际张拉力和吊杆实测1阶自振频率对吊杆第1次张拉阶段标定的吊杆索力比例系数、吊杆索力计算公式进行复核。

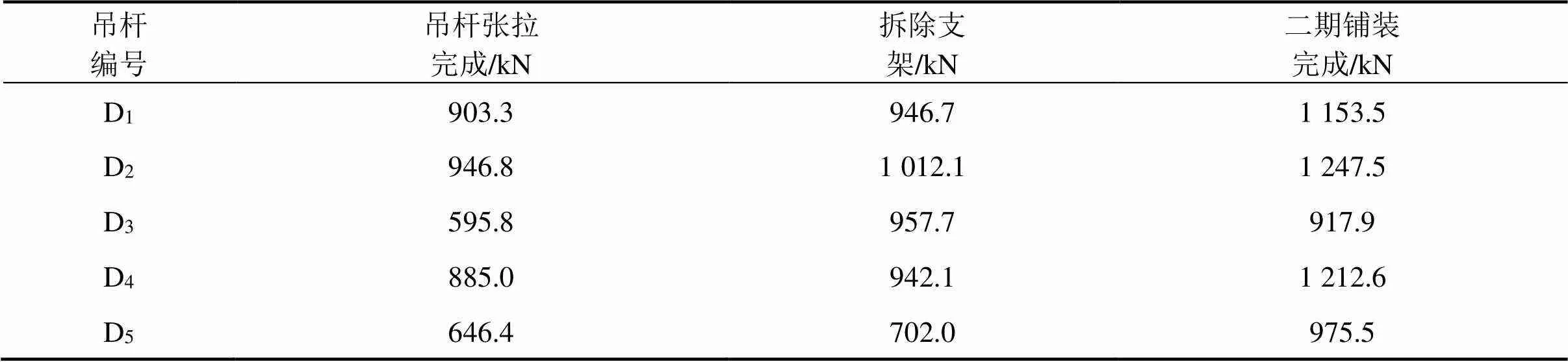
表2 各关键施工阶段吊杆索力设计值

3.3 吊杆有效长度计算

该桥吊杆与拱肋、系梁的连接方式为冷铸锚和锚箱。吊杆上锚固端构造如图2所示，下锚固端构造与上锚固端类似，吊杆上下锚固端锚固区长度分别为0.32 m和0.38 cm，张拉时在下端张拉。吊杆总长及有效长度如表3所示，表中各符号含义同式(17)，d取0.7 m。

表3 吊杆有效长度计算

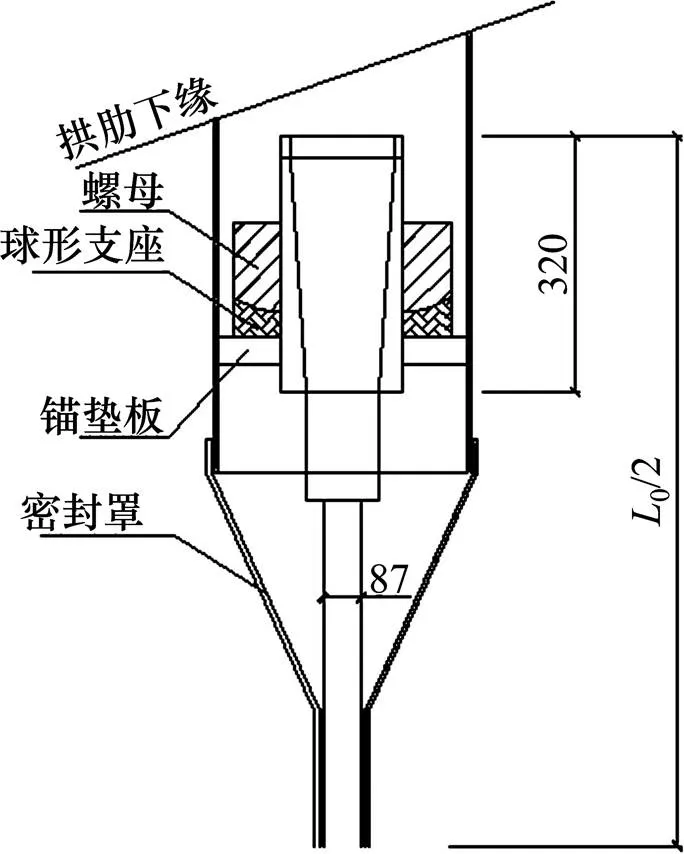
单位：cm

3.4 吊杆索力偏差系数η

吊杆拉压弹性模量=1.95×105MPa，线密度为=257 N/m，直径=0.087 m。该吊杆为PES(FD) 7-85平行镀锌高强钢丝，惯性矩计算采用移轴定理，将每根钢丝对其形心的惯性矩换算到吊杆截面形心，吊杆抗弯惯性矩为=2.049×10−6m4。将吊杆拉压弹性模量，抗弯惯性矩，有效长度代入式(12)可得到吊杆横向抗弯刚度修正值C，将C的值代入式(16)可求得吊杆索力偏差系数。各吊杆索力偏差系数的计算结果如表4所示，表中各符号下标为1表示计算时采用的吊杆有效长度为1，下标为2表示计算时采用的吊杆有效长度为2，为吊杆编号，bi表示吊杆索力比例系数标定阶段(吊杆第1次张拉阶段)各吊杆张拉力设计值，si表示二期铺装完成后各吊杆索力设计值，其余符号含义同上。

表4 吊杆索力偏差系数计算

由表4可知，均大于5%，为短吊杆，须用式(13)标定吊杆索力比例系数，用式(11)计算吊杆张拉完成后各施工阶段吊杆索力。

3.5 2种比例系数标定及吊杆索力计算公式的比较

在吊杆第1次张拉阶段(吊杆索力比例系数标定阶段)采集吊杆1阶自振频率，结合千斤顶油表读数，用式(3)标定吊杆索力比例系数K。吊杆第1次张拉阶段各吊杆的千斤顶张拉力T及吊杆1阶自振频率如表5所示。

在吊杆第1次张拉阶段用式(3)标定的吊杆索力比例系数K如表6所示，式中K为按弦振动理论计算的各吊杆索力比例系数，K表示基于弦振动理论标定的各吊杆索力比例系数，取1时表示计算时采用的吊杆有效长度为1，取2时表示计算时采用的吊杆有效长度为2，下标表示吊杆编号。从表6中可以看出，K与K之间的最大偏差为93%，即用2组比例系数计算得到的吊杆索力最大偏差为93%，在吊杆索力监测中如此大的偏差是不允许出现的，故在短吊杆索力测试计算中必须对吊杆索力比例系数进行标定。

表5 千斤顶张拉力及吊杆基频

表6 吊杆索力比例系数KiB的标定

将K代入式(4)可得在吊杆第1次张拉阶段基于弦振动理论标定的吊杆索力计算公式为：

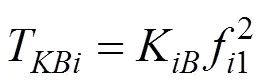
式中：T为编号为的吊杆的索力计算值；K为编号为的吊杆的吊杆索力比例系数标定值；f1为编号为的吊杆的1阶自振频率。

用式(13)在吊杆第1次张拉阶段标定的吊杆索力比例系数λK如表7所示，将各吊杆的λK及吊杆横向抗弯刚度修正值C代入式(11)可求得采用本文提出的吊杆索力比例系数标定、吊杆索力计算方法在吊杆第1次张拉阶段标定的各吊杆索力计算公式为：

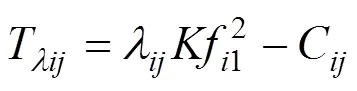
式中：T为编号的吊杆采用本文方法计算得到的各吊杆索力值；λ为编号的吊杆的边界条件修正系数；C为编号的吊杆抗弯刚度修正值；f1为编号的吊杆的1阶自振频率。上式中各符号的下标表示吊杆编号，下标取1时表示计算时采用的吊杆有效长度为1，取2时表示计算时采用的吊杆有效长度为2。

表7 吊杆比例系数λiK标定

吊杆第2次张拉阶段各吊杆实际张拉力T2i和实测1阶自振频率f1如表8所示。

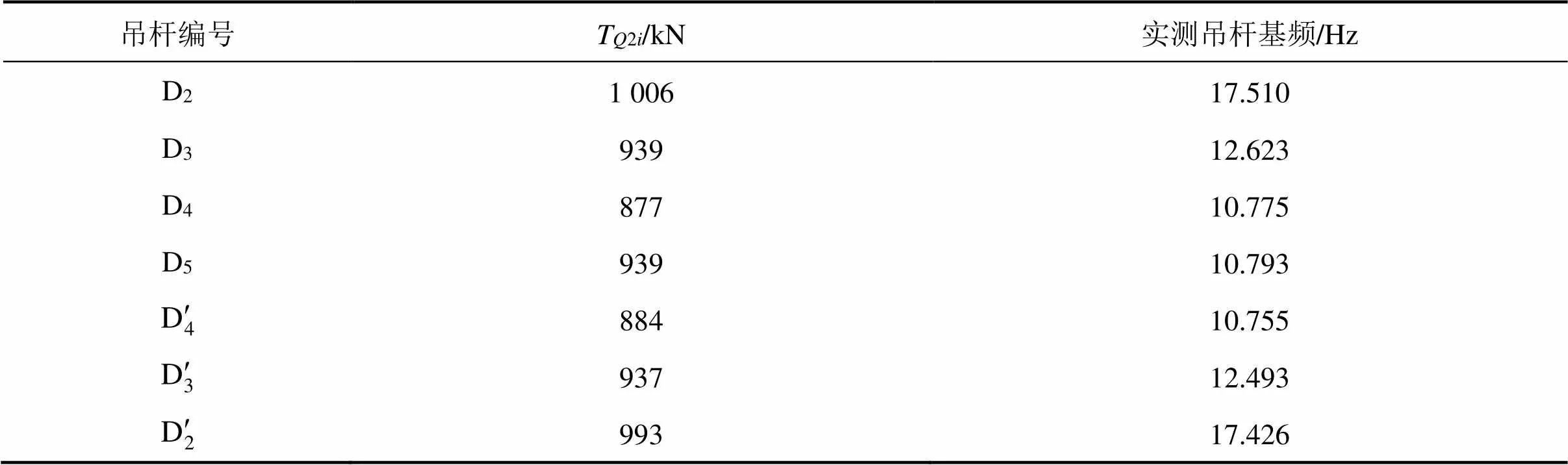
表8 吊杆第2次张拉阶段各吊杆千斤顶张拉力及吊杆基频

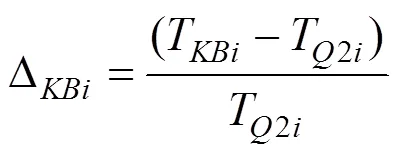
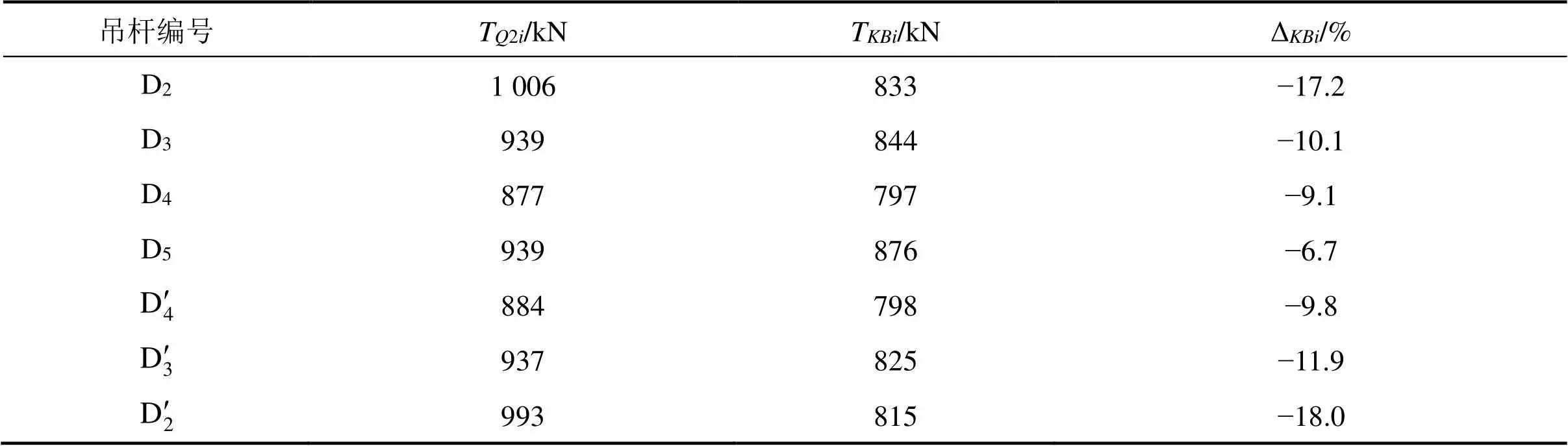
表9 式(18)的复核结果

由式(18)的复核结果表9可知：T小于T2i，两者之间最大偏差为−18%，最小偏差为−6.7%，偏差的绝对值大于吊杆索力计算控制误差Δ，证明基于弦振动理论的吊杆索力比例系数标定、吊杆索力计算方法在短吊杆索力监测中不可行。

由式(19)的复核结果表10可知：1)T2i与T1之间的最大偏差为−4.4%，T2与T2之间的最大偏差为−3.0%，偏差的绝对值均小于吊杆索力计算控制误差Δ，证明本文提出的吊杆索力比例系数标定、吊杆索力计算方法的合理性；2) 对比Δ1与Δ2，可以看出理论计算值T2与吊杆实际张拉力T2i更接近，说明本桥采用吊杆有效长度2较为合理。 3) Δ1与Δ2之间的最大偏差为1.5%，说明当吊杆与拱肋、系梁的连接方式为冷铸锚和锚箱时，吊杆有效长度的确定对吊杆索力比例系数标定、吊杆索力计算的影响很小。从表9和表10可以看出，本文提出的吊索力比例系数标定、吊杆索计算方法较基于弦振理论的吊杆索力比例系数标定、吊杆索力计算方法精度提高了13.4%，且吊杆总长越小，计算精度提高得越多，对于D5吊杆，精度仅提高了4.5%。

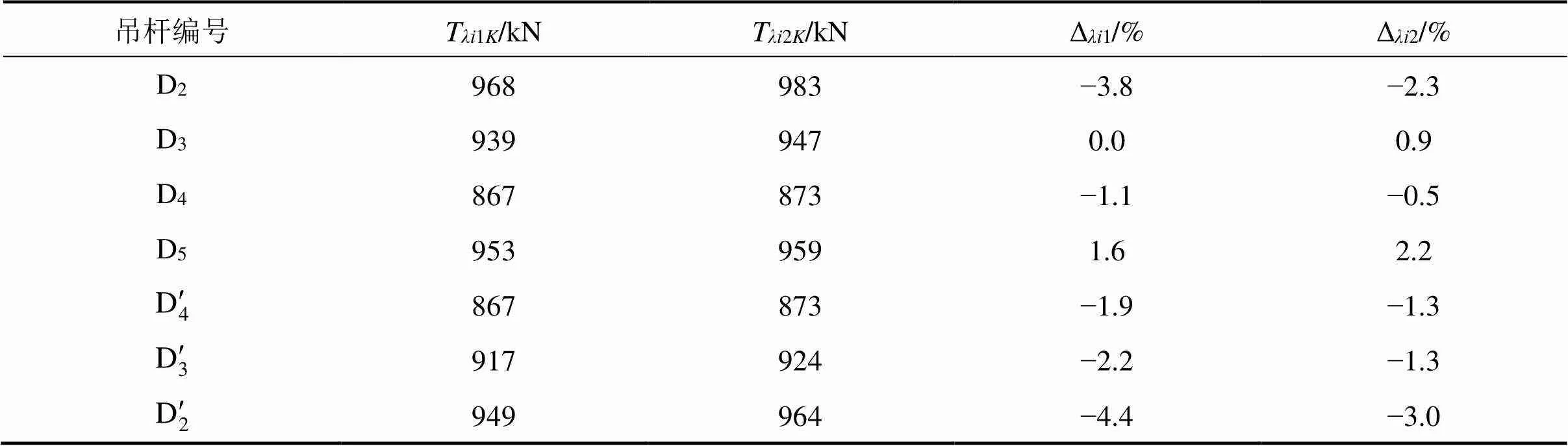
表10 式(19)的复核结果

第2次吊杆张拉完成后，采集各吊杆1阶自振频率，将其代入吊杆第1次张拉阶段标定好的吊杆索力计算公式式(19)计算各吊杆索力，以此作为第1次调索的依据。调索结果显示，吊杆索力计算值与该阶段吊杆索力设计值之间的偏差均在5%以内，再次说明本文提出的吊杆索力监测方法的合理性，具体调索计算在此不再赘述。

3.6 吊杆比例系数λK的2次复核

拆除系梁支架、桥面铺装完成后，采集各吊杆1阶自振频率代入吊杆第1次张拉阶段标定的各吊杆索力计算公式式(19)得到本阶段各吊杆索力，以此作为第2次调索的依据。第2次调索时，根据该阶段采集的吊杆1阶自振频率f1和吊杆实际张拉力T2i−2对吊杆第1次张拉阶段标定的各吊杆索力计算公式式(19)进行第2次复核。

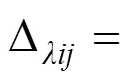
表11 2次调索千斤顶张拉力及吊杆基频

表12 式(19)的2次复核

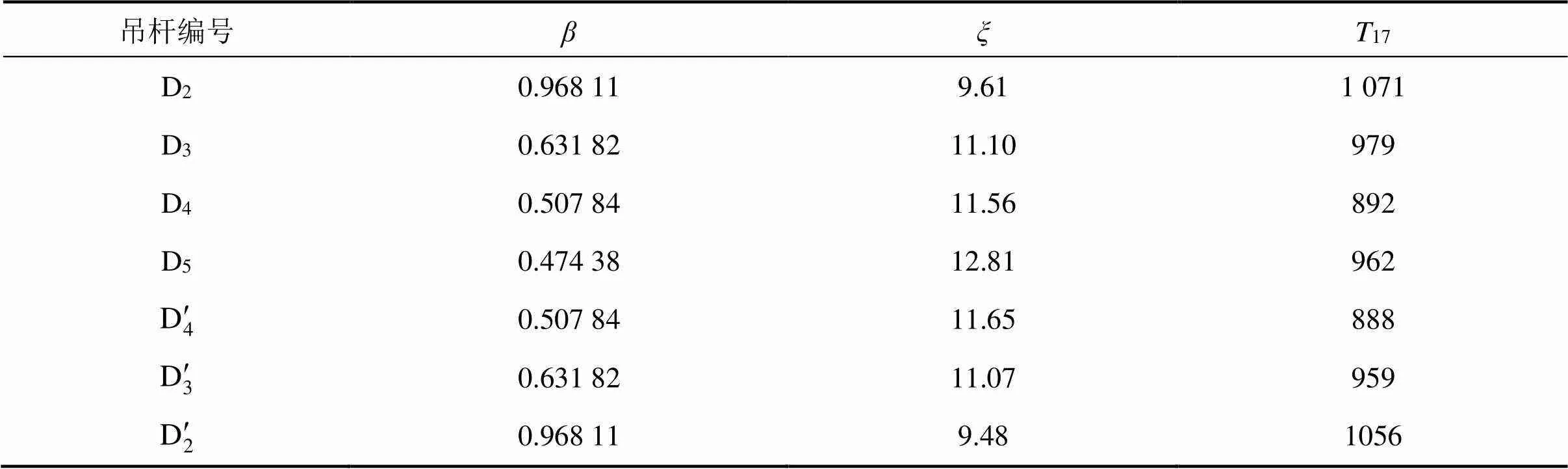
表13 吊杆第2次张拉阶段各吊杆索力计算值

3.7 短吊杆索力计算公式精度验证

采用文献[17]中的短吊杆索力计算公式及吊杆第2次张拉阶段各吊杆1阶自振频率计算该阶段各吊杆索力，并与表8中的T2i和表10的T2做比较，验证本文提出的吊杆索力比例系数标定、吊杆索力计算公式的可靠性。文献[17]中的短吊杆索力计算公式为：

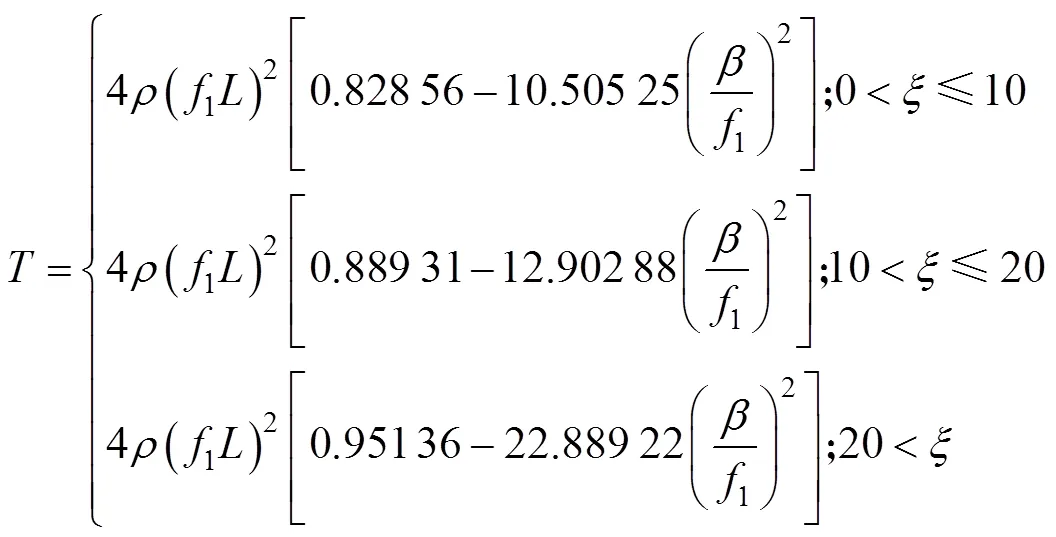
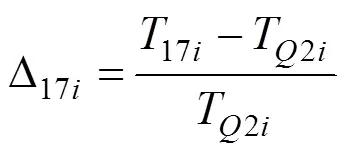
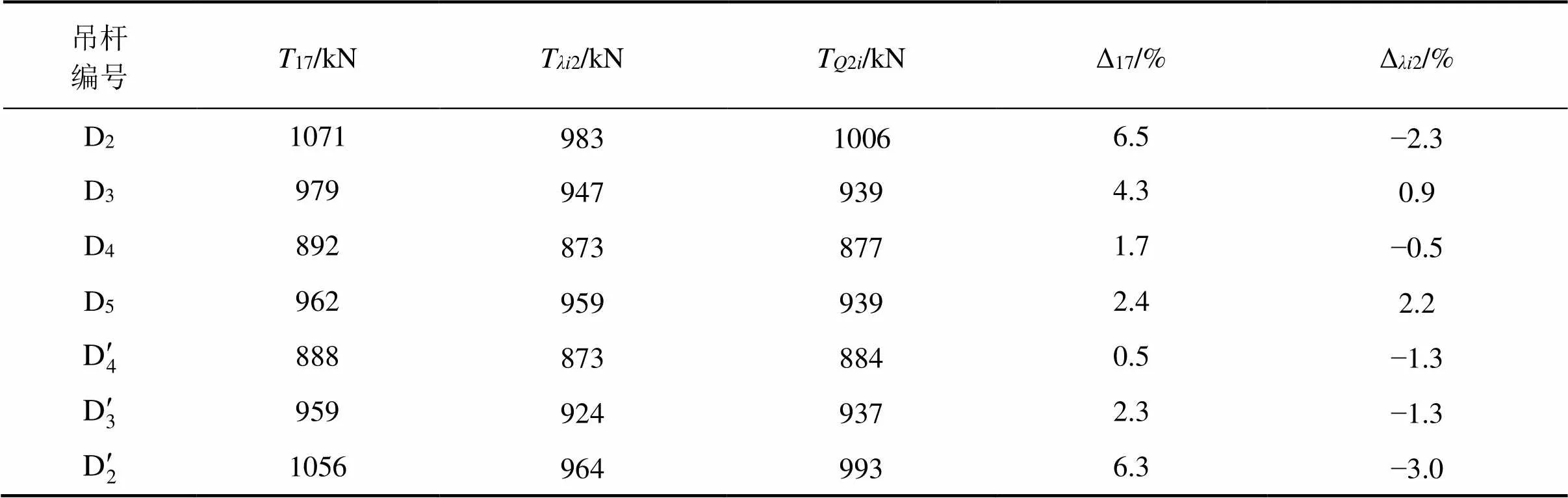
表14 计算精度对比

4 结论

1) 影响短吊杆索力测试精度的主要因素为吊杆两端边界条件的确定及吊杆横向抗弯刚度；在吊杆张拉过程中必须对吊杆索力比例系数进行标定和复核。

2) 引入吊杆索力偏差系数对短杆进行界定，对于短吊杆，本文提出的吊杆索力比例系数标定方法、吊杆索力计算公式相对于基于弦振理论的标定方法使短吊杆索力的计算精度提高了13.4%。

3) 采用本文提出的吊杆索力测试方法，吊杆有效长度的确定对吊杆索力测试的影响可忽略不计。

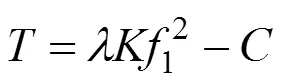
[1] 史杰, 姚君, 丁军. 基于静载试验标定拱桥吊杆索力计算长度研究[J]. 公路交通科技(应用技术版), 2017, 13(8): 262−264. SHI Jie, YAO Jun, DING Jun. Research on the calculation of suspender tension of arch bridge based on static load test[J]. Highway Technology of Transportation (Application Technology Edition), 2017, 13(8): 262−264.

[2] 薛刚, 孙树宝, 李建刚. 基于频率法的悬索桥锚跨索股索力测试分析[J]. 噪声与振动控制, 2017, 37(5): 154− 159. XUE Gang, SUN Shubao, LI Jiangang. Determing and analysis of suspender tension of anchor cables of suspension bridge based on frequency method[J]. Noise and Vibration Control, 2017, 37(5): 154−159.

[3] 于孟生, 郝天之, 陈齐风, 等. 基于频率法的质量块影响索力敏感性分析[J]. 建筑结构, 2017, 47(增1): 829− 832. YU Mengsheng, HAO Tianzhi, CHEN Qifeng, et al. Sensitivity analysis of influence of mass on suspender tension based on frequency method[J]. Building Structure, 2017, 47(Suppl 1): 829−832.

[4] 何雄君, 杨永超, 肖祥, 等. 基于有限元等效索长的振动频率法[J]. 桥梁建设, 2016, 46(6): 40−44. HE Xiongjun, YANG Yongchao, XIAO Xiang, et al. A vibration frequency method based on finite element equivalent suspender length[J]. Bridge Construction, 2016, 46(6): 40−44.

[5] 李晓章. 拱桥服役吊杆的力学性能退化及其索力识别研究[D]. 杭州: 浙江大学, 2015. LI Xiaozhang. Research on deterioration of mechanical properties of arch bridge service boom and identification of suspender tension[D]. Hanghou: Zhejiang University, 2015.

[6] 刘承斌, 胡志华, 蒋建群, 等. 频率法测试索力实验开发与实践[J]. 实验室科学, 2015, 18(2): 20−23. LIU Chengbin, HU Zhihua, JIANG Jianqun, et al. Development and practice of test of cable force by frequency method[J]. Laboratory Science, 2015, 18(2): 20−23.

[7] Kangas S, Helmicki A, Hunt V. Cable-stayed bridges: Case study for ambient vibration-based cable tension estimation[J]. ASCE Journal of Bridge Engineering, 2012, 17(6): 839−846.

[8] Robert Hong, Soliman Khudeira. Chicago’s first tied- arch bridge[J]. Practice Periodical on Structural Design and Construction, 2013.

[9] FENG Dongming, Thomas Scarangello, Maria Q, et al. Cable tension force estimate using novel noncontact vision-based sensor[J]. Measurement, 2017, 99(99): 44− 52.

[10] MA Lin. A highly precise frequency-based method for estimating the tension of an inclined cable with unknown boundary conditions[J]. Journal of Sound and Vibration, 2017,409(24):65 −80.

[11] BAI Ling, LIU Ke. Research on vortex-induced vibration behavior of steel arch bridge hanger[J]. Applied Mechanics and Materia1s, 2011(137):429−434.

[12] CHEN Qiang , LIU Lingyong. Research on mechanical property test of CFRP hanger in steel box arc bridge[J]. Advanced Materials Research, 2011, 1279(255−260): 3070−3076.

[13] Kim B H, Park T. Estimation of cable tension force using the frequency-based system identification method[J]. Journal of Sound and Vibration, 2007, 304(3−5): 660− 676.

[14] FANG Z, WANG J Q. Practical formula for cable tension estimation by vibration method[J]. Journal of Bridge Engineering, 2012, 17(1): 161−164.

[15] 袁梦. 大跨度系杆拱桥整体吊装施工过程若干关键技术研究[D].广州: 华南理工大学, 2015. YUAN Meng. Research on several key techniques in the whole hoisting construction process of large-span tied arch bridge[D].Guangzhou:South China University of Technology ,2015.

[16] 吴焕庆, 欧阳永金, 刘世忠. 频率法测连续梁拱桥吊杆索力影响因素研究[J]. 世界桥梁, 2013,41(4): 54−57. WU Huanqing, OUYANG Yongjin, LIU Shizhong. Research on influencing factors of suspension cable force of continuous beam arch bridge by frequency method[J]. World Bridges, 2013, 41(4): 54−57.

[17] 何容, 陈淮, 何伟. 考虑复合边界条件的中、下承式拱桥吊杆张力计算公式[J]. 中国铁道科学, 2012, 33(5): 15−21. HE Rong, CHEN Huai, HE Wei. Calculation formula of suspender tension of middle and lower arch bridge considering composite boundary conditions[J]. China Railway Science, 2012, 33(5): 15−21.

Determing short suspender tension based on frequency method

YAN Qiqing1, LIU Shizhong1, ZHU Zhanlong2, LI Dengke2

(1. Civil Engineering College, Lanzhou Jiaotong University, Lanzhou 730070, China;2. China Railway Northwest Research Institute Co., Ltd., Lanzhou 730070, China)

To improve the accuracy of the short suspender tension determined based on the frequency method, in combination with the relationship between suspender tension and its natural vibration frequency in the existing literature and through comprehensive analysis of the factors affecting the monitoring accuracy of the cable force of the boom, the boundary condition correction coefficient “” was introduced to correct the boundary conditions at both ends of the suspender. Based on the commonly used formula for calculating the tension of the suspender based on the frequency method，the stiffness parameter “” of the suspender was used to define the short suspender. A method for calibrating the suspender tension proportional coefficient considering the bending stiffness and boundary conditions of short boom and the suspender tension calculation formula were proposed. It was used for monitoring and controlling suspender tension of a 64 m through CFST tied arch bridge, which shows that compared with the traditional suspender tension calculation method, the use of this method improves the accuracy of the short suspender tension by 13.4%, and that the shorter the effective length of the boom, the greater improvement of the accuracy.

frequency method; determined short suspender tension; boundary conditions; flexural stiffenss; calibration of short suspender tension proportional coefficient