利用数学工具解决心房扑动波形融合问题
2020-11-12李艺袁杰陶凉
李艺 袁杰 陶凉
心房扑动(atrial flutter,AFL)是常见的心律失常,因与心房颤动关系密切,且同样存在临床症状及缺血性卒中风险,近年来逐渐受到临床关注。心电图是诊断AFL的金标准,但目前存在的问题是,由于心电图波形采集与记录的特点,心房除极波、心室除极波与心室复极波同时呈现在一维线性空间,故AFL发生时会不可避免地出现部分导联各种波形的相互叠加,房扑波可融入QRS波群中改变自身的振幅与形态,亦可融入ST-T段而难以辨认,融合后测量的部分波形间期(如QT间期)、振幅和形态可能使得其结果产生偏差。本研究将尝试使用数学工具对融合后的波形进行“拆分”,力图尽可能还原真实的波形图像。
1 波形拆分的理论基础
从物理学角度而言,当多列波在传播中相遇时,在该区域中质点的位移等于各列波单独传播时在该处引起位移的矢量和,这被称为波的叠加原理[1]。若把心电图波形看作二维时空中的波群,由于心电图记录方向是单向的(或可认为时间是单向的),则心房除极波、心室除极波及心室复极波可看作同向传导的波群,而大多数情况下,三者序贯出现且界限相对分明,可理解为3个波的频率是一致的。而当房性或室性心律失常等出现时,3个波会相互掩盖,可理解为由其中部分波的频率提高,与其他波形融合所致。根据波的叠加原理,在二维平面上融合波某点的位移取决于这3个波在某一时间上的矢量和,加之波形采集速度是固定的,所以最终决定融合波形态的只有融合点纵坐标(振幅)。融合点的纵坐标值等于非融合状态下多个波纵坐标的代数和。进一步可推导出,若房扑波与QRS波群及ST-T段融合时,只需要将此时融合区间上的波形的纵坐标减去对应房扑波的纵坐标,即可得到非融合状态下QRS波群及ST-T段的纵坐标。该原理亦是相关领域进行滤波操作的基本原理[2]。
2 图像处理方法
使用Matlab 2017(美国Mathworks公司)与Microsoft Excel 2010作为图像处理的主要软件。以1例AFL 4 ∶1下传的心电图为例:① 对目标导联心电图片段进行截取(图1),片段要求包括2个或2个以上的扑动波间期。② 将图片导入Matlab软件中,使用内部Haocurve工具(德国卡尔斯鲁厄理工学院开发,可从网上下载)提取曲线数据(图2)。值得注意的是,新建坐标系中横纵坐标的单位与范围可自定义,因为后面处理步骤所用的坐标参数均为相对值,且对于最终图形的生成无影响。③ 对坐标点进行仔细修正与评估,标测点(图2红点,扫描前页OSID码可查阅彩图)越密集,数据的提取与还原度越高。通过增减标测点以及调整位置,以房扑波周期为基准,尽量保证每个周期内标测点的数量差别不大即可(相等最佳)。④ 将修正后的标测点坐标导入Excel表格中,横坐标记录为序列x1,纵坐标记录为序列y1。此时需要在y1的坐标序列中找到相邻两个房扑波波谷(图2虚线方框内点集)的纵坐标的集合。因AFL折返环大而固定,周期稳定,故可复制多次两个波谷间的纵坐标序列(根据AFL比例确定),得到新的纵坐标序列y2。前文已述,无融合波形的纵坐标y3等于融合波形的纵坐标y1减周期性房扑波的纵坐标y2。⑤ 最终以x1为横坐标、y3为纵坐标,在Matlab或Excel中进行图形拟合,即可得到无房扑波融合的QRS-T波形(图3细线波形)。
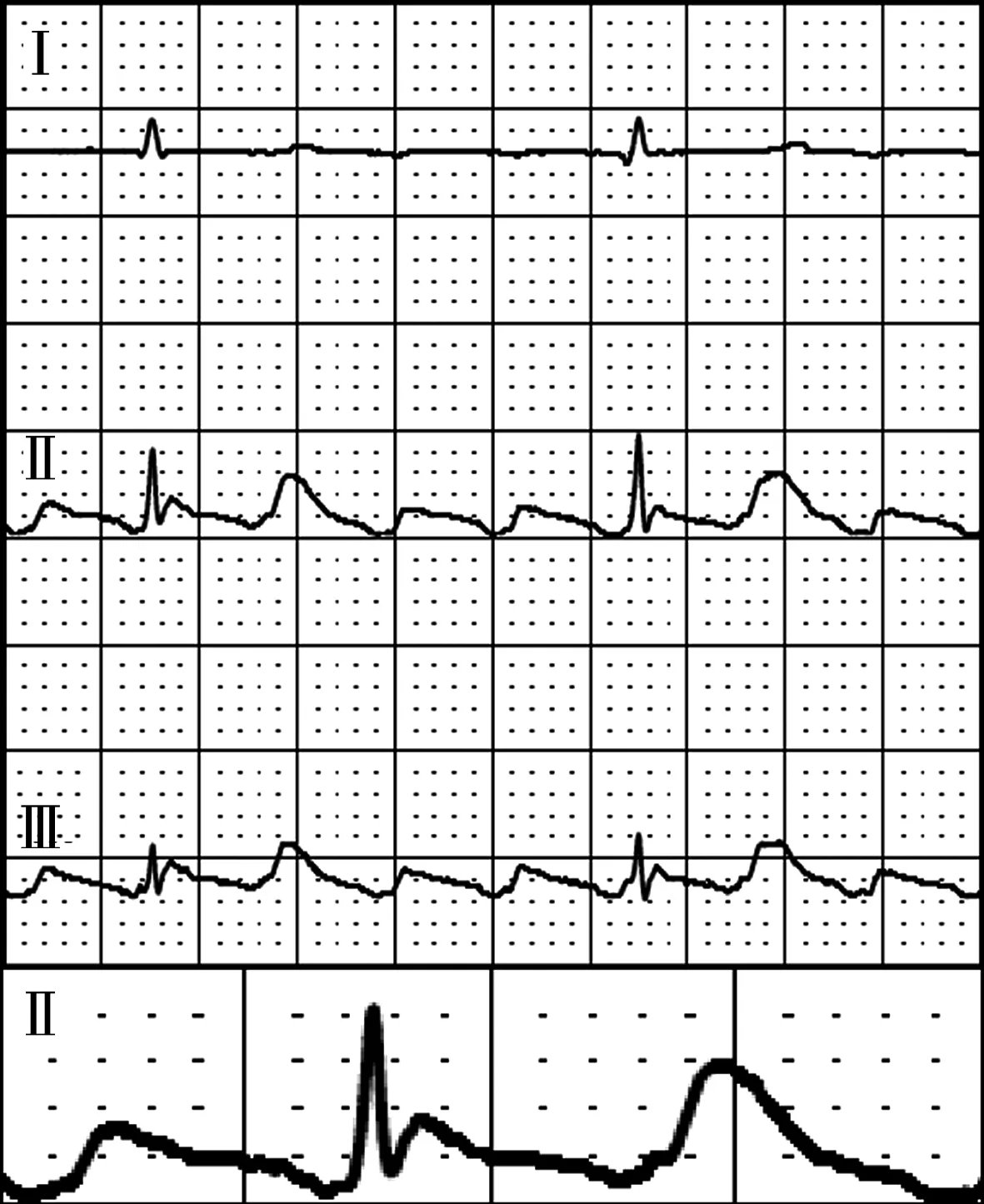
图1 截取1例心房扑动心电图的标Ⅱ导联片段
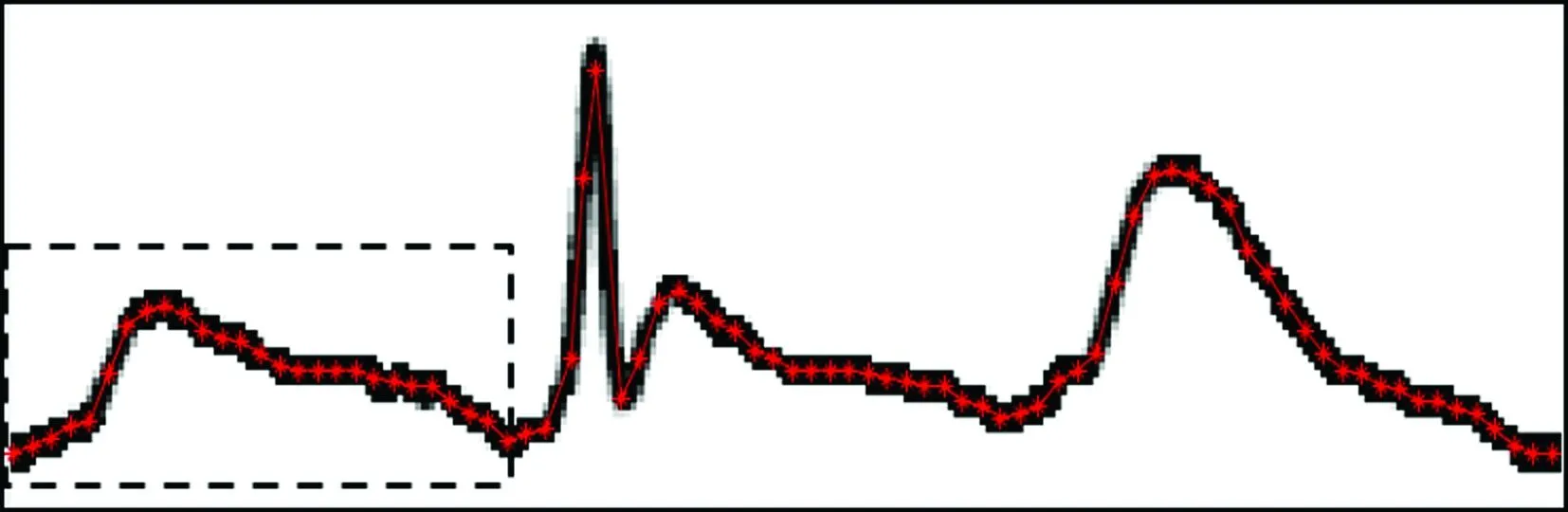
图2 使用Matlab对心电图波形进行标测及坐标(相对)提取
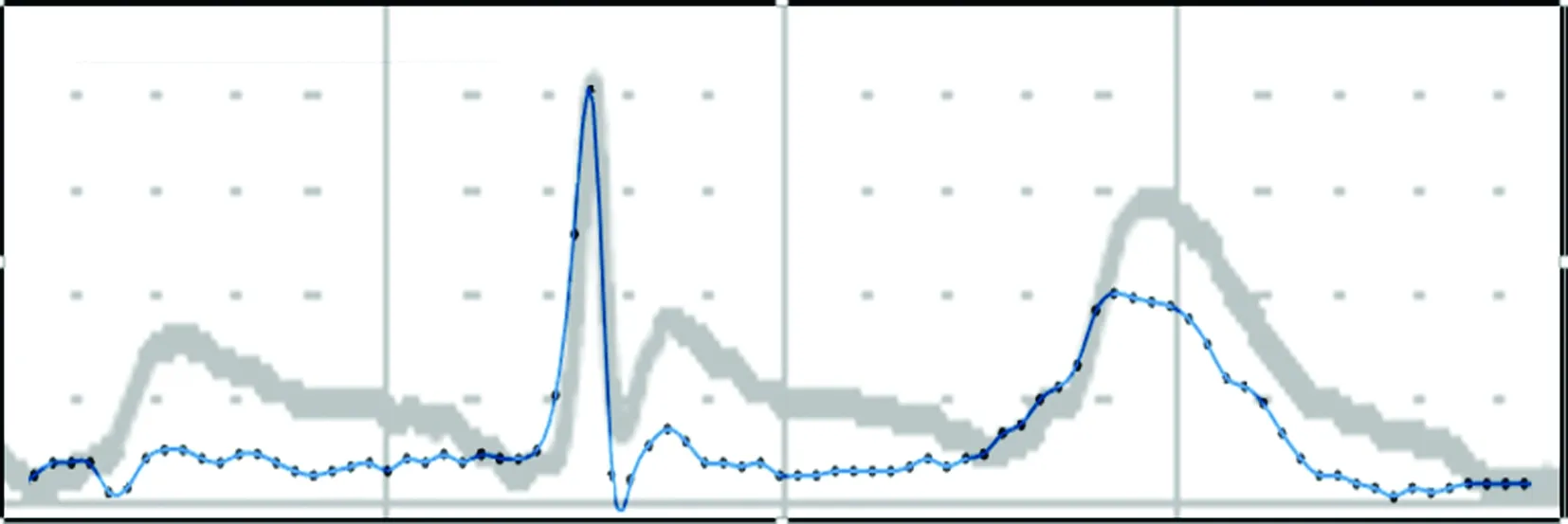
图3 分离出房扑波后的QRS-T波形与原图对比
3 肌袖性房性心律失常
肌袖性房性心律失常是一类起源于肺静脉或腔静脉壁上的心肌组织(肌袖)、具有独特心电图特征的心律失常。它主要表现为窦性心律的基础上,反复出现阵发性房速、房扑或房颤,且它们常相互转化。当成对房性早搏、房速出现时,P波往往以“PonT”的形式出现,与ST-T段形成融合。图4为1例肌袖性房性心律失常患者的心电图[3],图4A箭头所示部分房性P波叠加于其前的ST-T段之上。通过前文所述流程的处理后可见无P波叠加的ST-T段(图4C蓝色线条)。该案例提示,通过对比无P波叠加的ST-T段的形态,融合波拆分后的ST-T段在形态学上还原度较高。
4 心房扑动合并ST段压低的识别
AFL可损害房室机械协调性,从而影响心脏整体血流动力学状态,表现为心排量下降、肺循环负荷增加及诱发心肌缺血等,重者可出现心动过速性心肌病[4]。心电图的复极异常往往是心脏出现器质性改变的前兆,表现为ST段及T波的异常。而AFL的扑动波频率快且振幅大,往往可与ST-T段融合,使得难以准确评估后者情况。如图5A所示,经验丰富的医师可通过这份心电图发现QRS后可能存在ST-T改变,但因为房扑波的干扰,无法确切判断是否存在ST段压低及压低幅度等参数。我们使用前文所述的方法对其中一个QRS-T波进行处理,如图5B所示,可明显看到还原后的ST段(蓝色实线)较基线水平(虚线所示)明显压低,压低幅度>0.05 mV且合并T波低平,故应结合临床评估是否合并有慢性心肌缺血等情况。
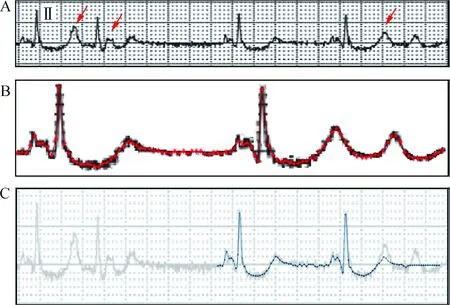
图4 肌袖性房性心律失常的波形融合处理效果
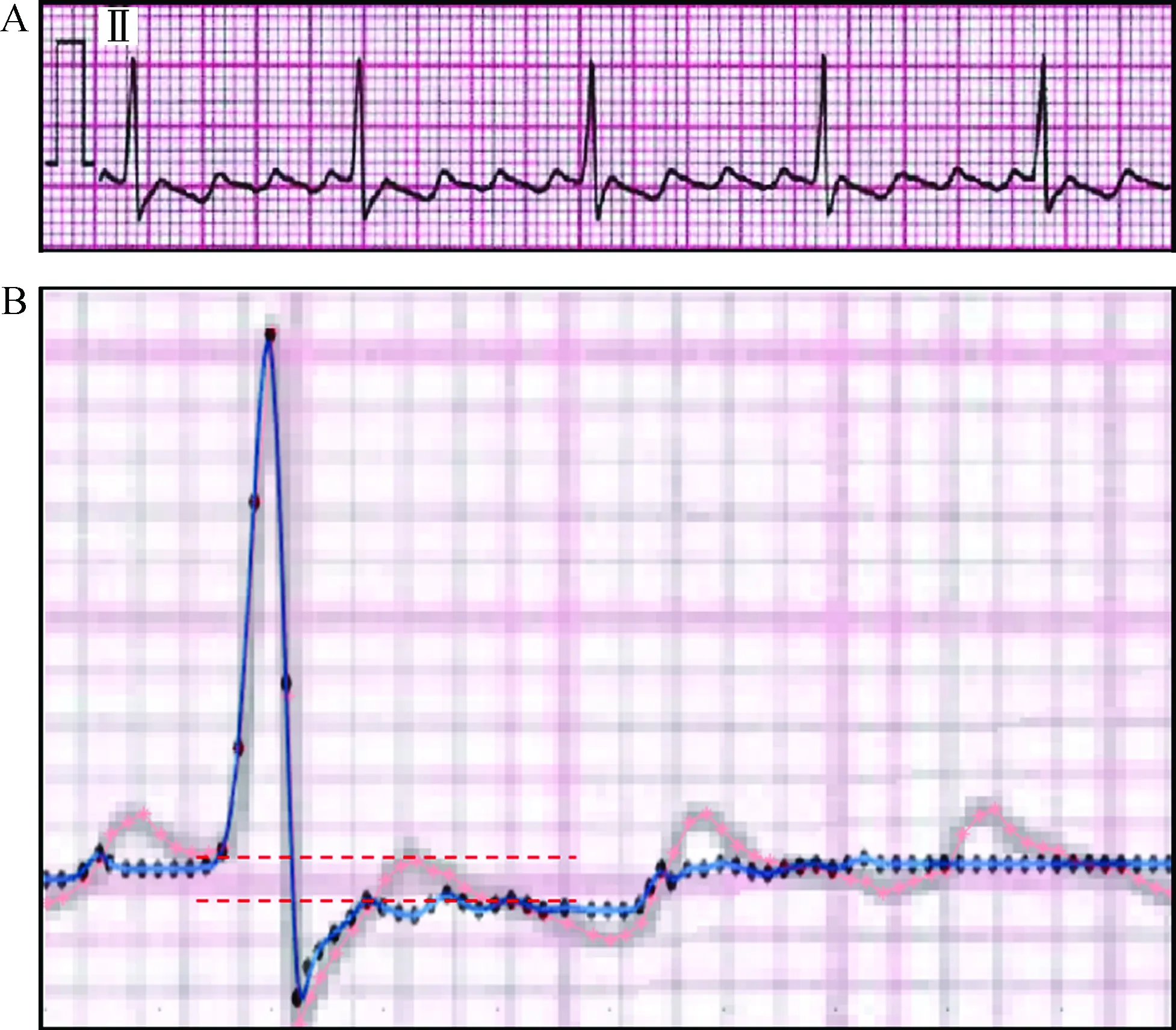
图5 心房扑动合并ST-T段改变
5 心房扑动2 ∶1下传
前文所进行的处理均为下传比例为4 ∶1的AFL。之所以选择较大比例,是因为比例越大,暴露出规律的房扑波越多,就越容易对扑动波的周期点位进行准确标测。然而AFL 2 ∶1下传时则是一个难点,因两个QRS波群之间仅有两个房扑波,且其中一个必然和ST-T段融合,这样就无法获得一个完整的房扑波周期(图6A)。但此时可以通过两个波谷或波峰(振幅可能不同)的间距得到扑动波的周期,用最高的波峰减最低的波谷可得到扑动波的振幅,那么我们可以通过人为补充或修正点位的方式预估一个完整周期的波形(图6B 箭头所示),余处理方法同前。随后亦可得到非融合状态下的QRS波群及ST-T段(图6C蓝色曲线所示)。
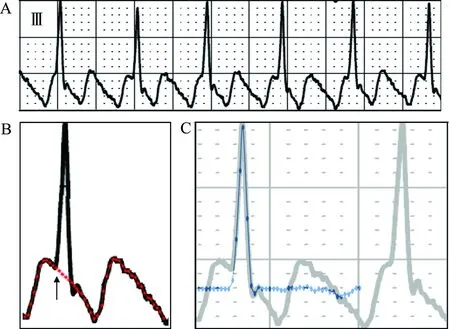
图6 心房扑动2 ∶1的波形融合处理
6 数学工具在心电图分析中的应用
首先,从数学角度而言,心电图本身可看作电压关于时间的一个连续函数,定义域为[0,+∞),而在短时间内频率相对固定,亦可进一步看作一个周期性函数,那么通过一些周期性函数的性质,可加深对心电图波形的研究与认识。傅里叶变换的核心思想为一切周期性波形可被分解为多个简单三角函数波形的形式[5],若应用到心电图波形的分析上,似乎可提供一个新的研究思路。其次,从物理学角度而言,心电图的图形又具有波的叠加性质,本研究即利用这一点对AFL的融合波形进行“拆解”。该方法适用于心电图上多种波与波的叠加情况,如帕金森患者心电图采集时基线大振幅周期性摆动、房性早搏未下传以及心脏移植后的双重心律的叠加等情况。但值得一提的是,传统心电图诊断上的诸多“融合波”,如室性融合波、心室预激等,并不能用此方法进行“拆分”,因为心室层面的融合波为心室内部各部分除极后产生波形的叠加,所以心电图记录的QRS波群和室性融合波的各组分属于包含与被包含的关系,拆分后的QRS并不是完整的心室除极图形,无诊断价值;而我们此前提到的应用领域中的各项波形融合前均为独立互斥的,故拆分后具有完整的波形诊断意义。最后,使用数学方法对心电图参数进行提取、再处理也同样能挖掘出更多有价值的信息。典型的例子便是近年来散点图的广泛应用,心电散点图是对24 h的RR间期与时间通过数学方法进行整合处理,以混沌理论为指导的一门具有重要临床价值的心电图诊断学分支;一方面大大提升了动态心电图的分析效率,另一方面对于复杂心律失常具有一定的鉴别诊断意义[6-7]。同样,动态心电图中的直方图、瀑布图以及叠加图等功能,也是利用数学工具对于已有的大数据进行整合重组,使其充分发挥应有的诊断价值。
7 总结与展望
目前,利用数学工具辅助心电图诊断已较为普遍,其本质是对现有心电图所包含的数据进行二次开发的过程。本研究尝试使用Matlab工具“拆分”AFL时扑动波与QRS-ST-T波形叠加状况,还原真实波形,为提高AFL时波形测量参数的准确性及部分心电异常诊断的敏感性提供新的技术思路。此技术拆解后的波形与真实波形吻合度的定量评估尚需要大样本的对照研究。我们认为,心电图记录本身即通过物理学手段将电信号转换为数学图形(波形)的过程,其蕴含的信息有较大的发掘空间,善用数学思维与工具则可事半功倍。
