“数形结合”理解一次函数

鲍聪晓

一次函数是刻画变量之间关系的数学模型.若要深刻理解一次函数，需要在一次函数的学习过程中巧用“数形结合”，以形助数、以数解形，增加思维的灵活性.

一、“数形结合”理解k與b

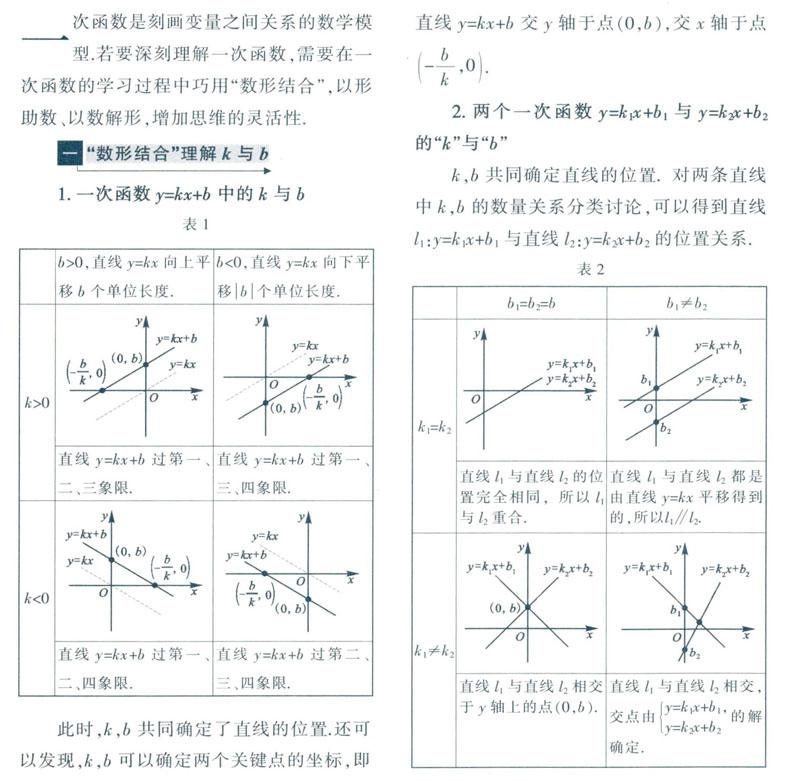
1.一次函数y=kx+b中的k与b

此时，k.b共同确定了直线的位置.还可以发现，k，b可以确定两个关键点的坐标，即直线y=kx+b交y轴于点（0，b），交x轴于点（-b/k，0）.

2.两个一次函数y=k1x+b1与y=k2x+b2的“k”与“b”

k，b共同确定直线的位置.对两条直线中k，b的数量关系分类讨论，可以得到直线l1：y=k1x+b1与直线l2：y=k2x+b2的位置关系.

二、一次函数与方程、不等式的关系

三、“数形结合”解决一次函数问题

例1 （2019年·毕节）已知一次函数y=kx+b（k，b为常数，k≠0）的图象经过第一、三、四象限，则下列结论中正确的是（ ）.

A.kb>0

B.kb<0

C.k+b>0

D.k+b<0

解析：一次函数y=kx+b的图象经过第一、三象限，k>0;又图象经过第四象限，b<0.故kb<0，选B.

例2 （2019年·梧州）直线y=3x+1向下平移2个单位，所得直线的解析式是（

）.

A.y=3x+3

B.y=3x-2

C.y=3x+2

D.y=3x-l

解析：选D.

例3 （2018年·遵义）如图1，直线y=kx+3经过点（2，0），则关于x的不等式kx+3>0的解集是（

）.

A.x>2

B.x<2

C.x≥2

D.x≤2

解析：直线y=kx+3与x轴的交点为（2，0）.kx+3>0，即y>0，对应的图象在x轴上方，不等式的解集为直线在x轴上方部分的横坐标.故不等式的解集为x<2，选B.

例4 （2019年·黔西南）如图2所示，一次函数y=ax+b（a，b为常数，且a>0）的图象经过点A（4，1），则不等式a+b<1的解集为_____.

解析：由函数y=ax+b的图象可知，直线经过点A（4，1），且自左向有，直线呈上升趋势，函数值y随x的增大而增大，故不等式ax+b<1的解集是x<4.

例5 （2018年·甘肃）如图3，一次函数y=-x-2与y=2x+m的图象交于点P（n，-4），则关于x的不等式组2x+m<-x-2，-x-2<0的解集为____.

解析：由2x+m<-x-2，知直线y=x-2在直线y=2x+m上方的部分满足不等式，即两直线交点左侧部分的横坐标满足不等式.然后将P点坐标代入已知的一次函数y=-x-2中，求出P（2，-4）.观察图象可得不等式的解集为x<2.

由不等式-x-2<0可知，直线y=-x-2在x轴下方的部分的横坐标满足不等式，即x>-2.

∴不等式组2x+m<-x-2，-x-2<0，的解集是-2<

-x-2<0x<2.

练习

1.（2019年·河池）函数y=x-2的图象不经过（

）.

A.第一象限

B.第二象限

C.第三象限

D.第四象限

2.把函数y=x的图象向上平移3个单位，下列各点中在平移后的直线上的是（

）.

A.（2，2） B.（2，3） C.（2，4） D.（2，5）

3.已知将直线y=x-1向上平移2个单位长度后得到直线y=kx+b，则下列关于直线y=kx+b的说法中正确的是（

）.

A.经过第一、二、四象限

B.与x轴交于点（1，0）

C.与y轴交于点（0，1）

D.y随x的增大而减小

4.如果一次函数y=-2x+m的图象经过点P（-2，3），且与x轴和y轴分别交于点A，B，则△AOB的面积是（

）.

A.1/2 B.1/4 C.4 D.8

5.（2019年·遵义）如图4，直线l1：y=3/2x+6与直线l2：y=-5/2x-2交于点P（-2，3）.不等式3/2x+615/2-2的解集是（

）.

A.x>-2 B.x≥-2 C.x<-2

D.x≤一2（答案在本期找）