一次函数与三角形面积

刘志峰

一、一条直线与两坐标轴围成的三角形

例1 已知直線y=2x-6与y轴和x轴分别交于点A，B，求△AOB的面积.

解：如图1，当x=0时，y=-6，所以直线y=2x-6与y轴交于点A（0，-6）;当y=0时，x=3，所以直线y=2x-6与x轴交于点B（3，0）.

因此OA =6.OB=3.

∴S△AOB=1/2·OA ·OB=9.

练习1.已知直线y=2x+b与x轴和y轴分别交于点A，B，且△AOB的面积是9.求6的值.

2.已知直线y=kx-6与x轴和y轴分别交于点A，B，且△AOB的面积是9.求k的值.

（答案在本期找）

总结：解一条直线与坐标轴围成的三角形的面积问题的步骤是：①求出直线与坐标轴的交点坐标;②根据三角形面积公式列方程;③解方程，求出未知数的值，

例2 一次函数y=kx+b的图象经过点A（3，0），且与两坐标轴围成的三角形AOB的面积是9.求该一次函数的解析式.

解：一次函数y=kx+b的图象与y轴交于点B（O，b），则OB=|b|.

由已知条件知OA=3.

因此S△AOB=1/2·3·|b|=9，解得b=+6.

∴一次函数的图象经过点（3，0），（0，6）成点（3，0），（0，-6），其解析式为y=-2x+6或y=2x-6.

例3 已知点A（8，0）及在第一象限的动点P（x，y），且x+y=10.设△OPA的面积为S.

（1）求S关于x的函数关系式.

（2）求x的取值范围.

（3）画出S关于x的函数的图象.

（4）当P点在什么位置时，S=12？

解：（1）根据题意知OA=8.

∵点P（x，y）在第一象限，

∴点P（x，y）到OA边的距离为y.

∴S=1/2·8·y=4y.

又x+y=10，故S=-4x+40.

（2）因点P（x，y）在第一象限内，故得x>0，10-x>0，即0

（3）如图2.

（4）当S=12时，有-4x+40=12，x=7.

又因x+y=10，故y=3.

因此当P点坐标为（7，3）时，S=12.

二、两条直线与坐标轴围成的三角形

例4 求直线y=2x-6，y=-2x+2与x轴围成的三角形的面积.它们与y轴围成的三角形的面积呢？

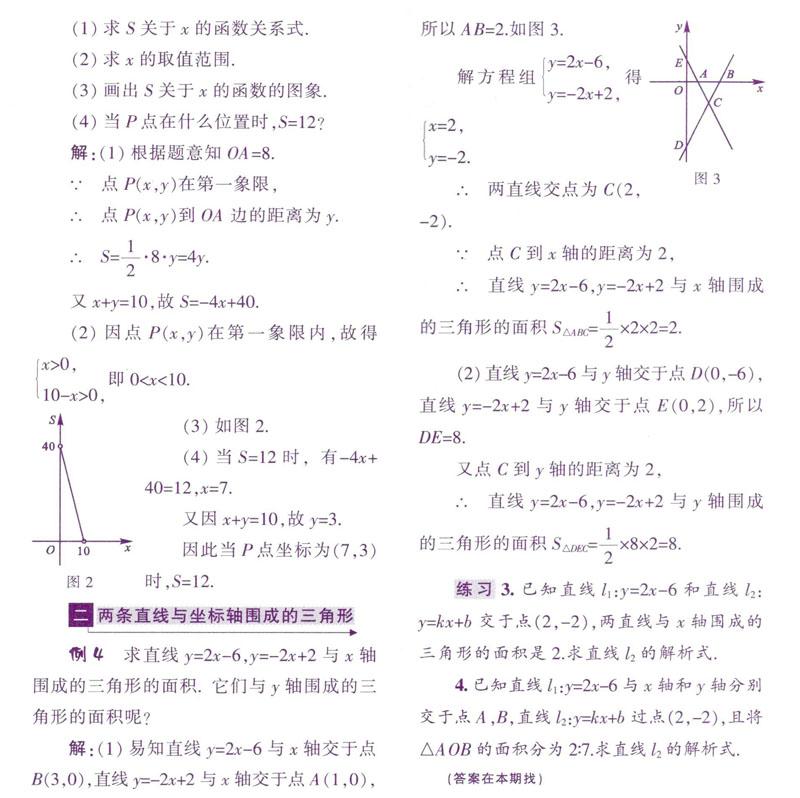
解：（1）易知直线y=2x-6与x轴交于点B（3，0），直线y=-2x+2与x轴交于点A（1，0），所以AB=2.如图3.

解方程组y=2x-6，y=-2x+2，得x=2，y=-2.

∴两直线交点为C（2，-2）.

∵点C到x轴的距离为2，

∴直线y=2x-6，y=-2x+2与x轴围成的三角形的面积S△ABC=1/2×2×2=2.

（2）直线y-2x-6与y轴交于点D（O，-6），直线y=-2x+2与y轴交于点E（0，2），所以DE=8.

又点C到y轴的距离为2，

∴直线y=2x-6，y=-2x+2与y轴围成的三角形的面积S△DEC=1/2×8×2=8.

练习3.已知直线l1：y=2x-6和直线l2：y=kx+b交于点（2，-2），两直线与x轴围成的三角形的面积是2.求直线l2的解析式.

4.已知直线l1：y=2x-6与x轴和y轴分别交于点A，B，直线l2：y=kx+b过点（2，-2），且将△AOB的面积分为2：7.求直线l2的解析式.

（答案在本期找）