不解藏踪迹，动点一道开

周跃佳

[摘  要] 文章以2020年全国Ⅰ卷中的解析几何压轴题为载体，以GeoGebra为探究工具，展示直线过定点问题探究解答的基本思维，并以动点联动的过程探索高考命题的背景和问题的本质，为相关试题的命制提供更广阔的思路.

[关键词] GeoGebra;解析几何;极点极线

解析几何中高度抽象的联动关系，运动变化中的变与不变关系，难以被直观感知.让技术助力数学表征，挖掘更深层次的数学背景，促进学生深度学习，为探索规律启发思路，建立“意会”与“言传”之间的交流障碍. 文章从2020年一道解析几何试题的解法分析入手，借助GeoGebra揭示其清晰的几何直观、动态变换和深刻的数学背景，促成问题的解决和知识的延伸.

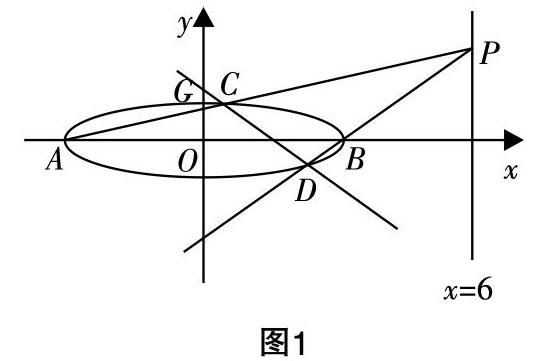
引例：（2020年全国Ⅰ卷理20/文21）已知A，B分别为椭圆E：■+y2=1（a>1）的左、右顶点，G为E的上顶点，■·■=8. P为直线x=6上的动点，PA与E的另一交点为C，PB与E的另一交点为D.

（1）求E的方程;（解答略，答案：■+y2=1.）

（2）证明：直线CD过定点.

动点探位

P点为整个运动过程中的主动点，它在直线x=6上运动，使得C点和D点随之变化，但奇怪的是，无论怎么变，直线CD总过一个定点.可以让点P动到某个特殊位置时，初步判断定点的位置.当点P到达x轴上的时候，直线CD也与x轴重合，说明我们寻求的定点在x轴上，可以将直线CD方程设为x=my+n，求出n即求出了直线所过定点，这是高考参考答案给出的方法（此处略去解答）.

主“动”出“机”

通过GeoGebra作图后，可以清晰地看到主动与被动变化过程中直线恒过定点这一事实. 可以从主动点出发，设置变量，表示出与被动点的变化关系，从而找到突破的机会. 由于主动点P在直线x=6上运动，真正变化的只有其纵坐标，将坐标设出来即可把直线PA和PB的方程表示出来，进而与椭圆方程联立求出C，D两点坐标，表示出CD的方程.

由（1）知A（-3，0），B（3，0），设P（6，t），则直线PA的方程为：y=■（x+3），

联立直线PA的方程与椭圆方程：y=■（x+3），■+y2=1，整理得：

（t2+9）x2+6t2x+9t2-81=0.

由韦达定理-3x■=■，得x■=■，

代入直线PA的方程y=■（x+3）得，yC=■，即C（■，■）.

直线PB的方程为y=■（x-3），

联立直线PB的方程与椭圆方程：y=■（x-3），■+y2=1，整理得：

（t2+1）x2-6t2x+9t2-9=0.

由韦达定理3xD=■得xD=■，代入直线PB的方程y=■·（x-3）得，yD=■，即D■，■，

所以直线CD的斜率k■=■=■，

所以直线CD的方程为y-■=■x-■，

整理得y=■x-■，所以直线CD过定点■，0.

动与不动，谁在“管控”

题目解答完毕后，我们不停留于此.提出以下问题：为什么直线CD总过一个定点？椭圆方程会影响直线定点吗？直线x=6会影响直线定点吗？这个问题可以拓展吗？通过GeoGebra作图后，我们让椭圆方程■+■=1中的a和b以及点P所在直线分别变动起来，试图探求影响直线过定点的因素，获得命题背后的本质.

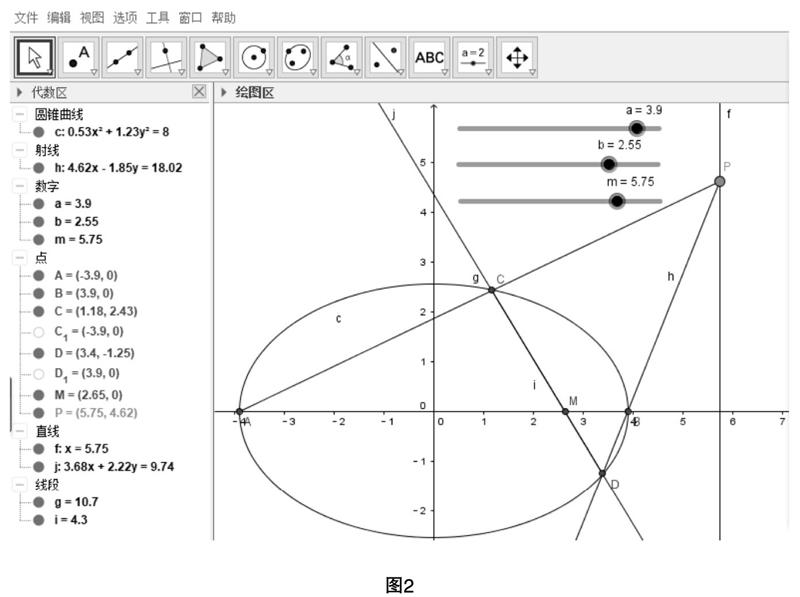
1.？摇探索a和b对直线过定点的影响（图2）

通过制定滑动条按钮，发现a的变化会影响直线CD过定点的变化，而b的变化不会影响直线CD过定点的变化.

2.？摇探索点P所在直线对直线过定点的影响

用同样的方法，在GeoGebra中改变直线x=6的值，发现直线CD过定点发生变化.说明椭圆方程中a的值和点P所在直线共同影响直线CD过定点.在变化的过程中，我们发现了以下特征.

猜想与证明：

结论1：已知A，B分别为椭圆E：■+■=1（a>b>0）的左、右顶点，P为直线x=m上的动点，PA与E的另一交点为C，PB与E的另一交点为D，直线CD过定点■，0.

证明方法与引例解答方法一致，命题成立.

初步拓展：

结论2：已知A，B分别为椭圆E：■+■=1（a>0，b>0）的上、下顶点，P为直线y=m上的动点，PA与E的另一交点为C，PB与E的另一交点为D，直线CD过定点0，■.

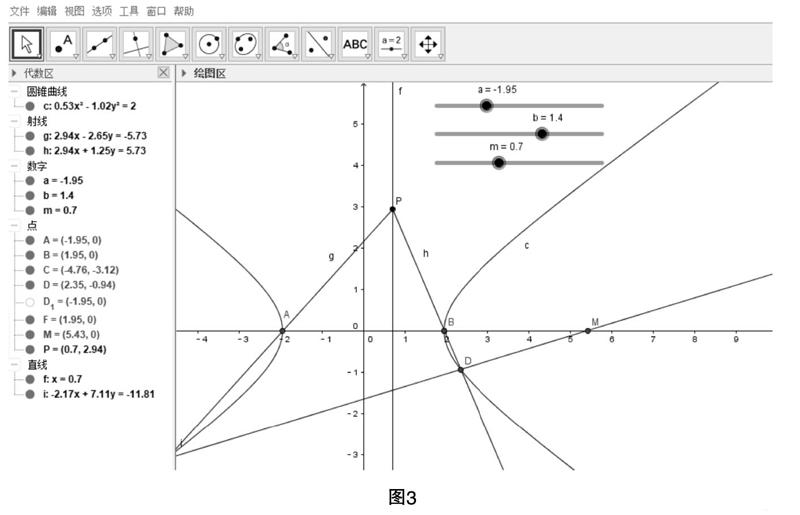
下面，看看双曲线中是否具有类似特征（图3）.

通过探索，我们发现在双曲线中具有以下结论：

结论3：已知A，B分别为双曲线E：■-■=1（a>0，b>0）的左、右顶点，P为直线x=m上的动点，PA与E的另一交点为C，PB与E的另一交点为D，直线CD过定点■，0.

结论4：已知A，B分别为双曲线E：■-■=1（a>0，b>0）的上、下顶点，P为直线y=m上的动点，PA与E的另一交点为C，PB与E的另一交点为D，直线CD过定点0，■.

椭圆、双曲线统一定理

1.已知A，B分别为圆锥曲线E：Ax2+By2=1（A>0）的左、右顶点，P为直线x=m上的动点，PA与E的另一交点为C，PB与E的另一交点为D，直线CD过定点■，0.

2.已知A，B分别为圆锥曲线E：Ax2+By2=1（B>0）的上、下顶点，P为直线y=m上的动点，PA与E的另一交点为C，PB与E的另一交点为D，直线CD过定点0，■.

深度拓展

圆锥曲线的极点、极线统一定理：

极点、极线定义：已知圆锥曲线C：Ax2+Cy2+2Dx+2Ey+F=0（A2+B2≠0），则称点M（x■，y■）和直线l：Ax■x+Cy■y+D（x■+x）+E（y■+y）+F=0是圆锥曲线C的一对极点和极线.

本题中直线x=m为椭圆E：■+■=1（a>b>0）的一条极线，直线CD所过定点M■，0即为对应的极点.若點P为极线l上的动点，PA与E的另一交点为C，PB与E的另一交点为D，直线CD过极点M.反之，过极点M的直线与椭圆交于C，D两点，则直线AC与BD的交点P在极线上.

相关试题命制：

1.已知A，B分别为椭圆E：■+y2=1的左、右顶点，过点M（2，0）的直线与椭圆交于C，D两点，证明：直线AC与BD的交点在一条定直线上.

2.已知椭圆E：■+■=1，过点M（2，0）的直线与椭圆交于C，D两点，椭圆在C，D两点处的两条切线交于点P，证明：点P在一条定直线上.

3. 已知椭圆E：■+■=1，若点P为直线l：x=4上的动点，过点P作椭圆的切线，切点为C，D两点，证明：直线CD过定点.

同样，可以基于圆锥曲线的极点和极线命制双曲线、抛物线的相关试题.