关注知识综合,聚焦方法策略
2020-11-06苗晓丽
苗晓丽


[摘 要] 反比例函数与几何综合题在中考中十分常见,问题的考查内容、命制形式、解析方法具有极高的研究价值,对问题开展教学探究有利于培养学生的数学思维. 文章对问题背景进行探讨,结合实例开展思路突破、拓展探究,提出相应的教学建议.
[关键词] 反比例函数;几何综合;图像;模型;数形结合
问题背景
反比例函数是初中数学的重点知识,需要掌握其性质和图像,而中考常综合考查反比例函数和几何知识,以常见的动点、平移、翻折、存在性等形式命题. 其问题类型多样、难度较大,对学生的知识理解、方法掌握和解题思想有着较高的要求. 反比例函数与几何综合的突破关键为点坐标,由点坐标可以确定反比例函数曲线,而结合几何点则可以建立几何图形. 对于该类综合题有以下两种突破思路:一是从关键点或线段入手,联系点坐标和直线线段进行互化,联合探究反比例函数与几何特征;二是转化、整合函数与几何特征,构建相应的方程,或将问题转化为相应的函数模型,利用对应性质来探究突破.
问题探究
中考中常见反比例函数与几何的综合题,其设问形式和解析思路均具有一定的代表性,具有极高的研究价值,下面以2019年江苏省徐州市的一道压轴题为例开展解题探究.
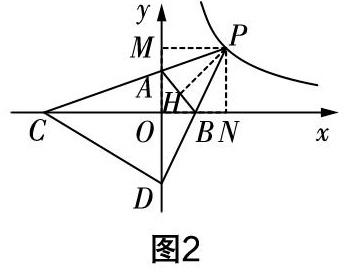
(2019年江苏省徐州市中考卷第28题)平面直角坐标系中,O为原点,点A,B分别在y轴、x轴的正半轴上. △AOB的两条外角平分线交于点P,P在反比例函数y=■的图像上. PA的延长线交x轴于点C,PB的延长线交y轴于点D,连接CD.
(1)求∠P的度数及点P的坐标;
(2)求△OCD的面积;
(3)△AOB的面积是否存在最大值?若存在,求出最大面积;若不存在,请说明理由.
思路突破 本题目主要考查反比例函数的性质、角平分线的性质和几何三角形等相关知识,解题的关键是把握函数与几何的关联点——点坐标,合理构建模型来转化突破,对于其中的面积问题则需要充分结合面积公式,合理采用面积模型的构建方法进行转化解析.
解析 (1)该问求∠P的度数及坐标,需要充分利用角平分线的性质,以及三角形内角和定理. 已知AP和BP分别为△AOB的两条外角平分线,则∠PAB=■∠BAY,∠PBA=■∠ABX,所以∠PAB+∠PBA=135°,则∠APB=45°. 过点P作AB的垂线,垂足为点H,再过点P分别作x轴和y轴的垂线,垂足分别为N和M,如图2所示. 分析可证△PMA≌△PHA,△PNB≌△PHB,所以PM=PN. 根据反比例函数解析式可设点P的坐标为a,■,则a=■,可解得a=3,所以点P的坐标为(3,3).
(2)该问求△OCD的面积,首先需要理解三角形构建的过程,是两条角平分线的延长线与坐标轴的交点,求三角形面积应从关键点或关键线段入手. 由于△OCD为特殊的直角三角形,则其面积可以表示为S■=■·OC·OD,显然解题的关键是确定OC和OD,可以求线段长,也可以直接确定OC·OD的值.
结合条件分析可知不易直接求点C和点D的坐标,故需要求OC·OD的值,可将其视为相似三角形对应边成比例的一部分. 连接OP,并按照图3标识角度. 分析可知∠7+∠8=45°,又知PM∥BC,PN∥OM,则∠3=∠7,∠4=∠8,所以∠3+∠4=45°,同理可证∠1=∠4,所以△POC∽△DOP,由相似性质可得■=■,则OP2=OC·OD,从而有OC·OD=18,所以S■=■·OC·OD=9,即△OCD的面积为9.
(3)该问探讨△AOB的面积是否有最大值,三角形面积最值探究一般需要利用函数或不等式性质,因此可以采用如下思路:整合几何特性,结合面积公式将问题转化为关于线段长或坐标参数的面积函数,通过函数分析来确定最值.
设BN=x,AM=y,则OA=3-y,OB=3-x,由(1)问可知AB=x+y,在Rt△AOB中使用勾股定理可得(3-x)2+(3-y)2=(x+y)2,整理可得y=■,所以S■=■(3-x)(3-y)=■. 设■=k,整理可得x2+(k-3)x+3k=0. 由于x为实数,则Δ=(k-3)2-12k≥0,可解得k≥9+6■或k≤9-6■,△AOB的面积小于9,则k≤9-6■,所以S■有最大值27-18■,即△AOB的面积存在最大值,且为27-18■.
评析 上述反比例函数与几何综合题主要考查几何面积,解析时需充分利用函数与几何的性质. 其中第(2)问构造了相似三角形,利用相似性质来转化条件;而第(3)问则利用面积模型将问题转化为面积函数及方程,利用一元二次方程根的判别式来分析函数的最大值. 总体来看,问题突破过程中需要充分把握函数与几何特性,借助函数及方程性质来分析转化.
拓展探究
上述考题主要探讨反比例函数与几何面积,属于反比例函数背景下的面积问题,而反比例函数与几何综合的考查视角较多,几何特性判断是另一重要考查内容,问题解析时需要充分把握几何特性与函数性质间的关联,下面举例探究.
(2018年浙江省金华市中考卷第23题)如图4所示,四边形ABCD的四個顶点分别在反比例函数y=■与y=■(x>0, 0 (1)当m=4,n=20时. ①若点P的纵坐标为2,求直线AB的函数表达式; ②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由. (2)四边形ABCD能否成为正方形?若能,求此时m,n之间的数量关系;若不能,试说明理由. 解析 本题目考查反比例函数背景下几何图形的形状,需从几何特性出发来探讨.
(1)①该问求直线AB的表达式,只需要提取反比例函数图像上点A和点B的坐标即可,可求得y=■x+3.
②该问探讨四边形ABCD的形状,需要根据点坐标来确定线段长,由线段长度关系来分析几何形状. 易得B(4,1),D(4,5),则点P(4,3),分析可得PA=PC=■,又知PB=PD,所以四边形ABCD为平行四边形;又知BD⊥AC,则四边形ABCD为菱形.
(2)该问探究四边形ABCD能否为正方形,根据几何特性可知需有PA=PB=PC=PD(设为t>0). 分析可得点B坐标为4,■,则点A坐标为4-t,■+t,所以(4-t)■+t=m,化简得t=4-■,则点D的纵坐标值为8-■,所以点D的坐标为4,8-■.则4·8-■=n,整理可得m+n=32,即四边形ABCD为正方形时有m+n=32.
评析 上述综合题以反比例函数为背景考查特殊图形的性质,解析时充分把握平行四边形对角线互相平分、正方形对角线互相平分且相等的特性,而后联合点坐标来构建相应的代数关系,从而高效解题.
教学建议
1. 夯实基础,方法积淀
反比例函数与几何考题属于综合性问题,其中涉及函数的性质与图像、几何定理定义、性质变换等基础知识,问题形式和知识背景变换多样,但考查内容均大同小异,解题的方法技巧是相通的. 开展考题探究需要从问题所涉的基础知识、基本方法和基本思想入手,处理好通法和技巧之间的关系,合理构建类型问题的突破思路. 例如上述问题的突破充分利用了函数与几何的性质,把握点坐标与几何特性之间的联系,以此作为突破口开展解析推导,同时融合待定系数法、交点坐标法、代数方程法等方法技巧. 因此在教学中教师需要引导学生关注问题的考查内容,夯实基础知识,归纳总结知识技巧,进行解题方法的積淀,从根本上提升学生的能力.
2. 延伸拓展,开放思维
把握问题内容的主干,在此基础上开展拓展训练,有助于学生对问题的理解,培养学生思维的灵活性和广阔性. 例如上述“拓展探究”阶段中从反比例函数与几何形状入手开展问题探究,让学生对该类型综合题的考查视角有了更深刻的认识,总结了相应的突破思路. 在拓展探究过程中还体现了数学的拓展迁移方法,对于培养学生的数学思维有着一定的帮助. 因此在实际教学中,教师应引导学生开展问题拓展延伸,从问题的内容、解法入手进行深度教学,让学生感知问题中融合的思想方法,感悟通法解题的优势所在.
3. 承启高中,数形结合
函数与几何问题是中学数学知识融合的典型代表,该类问题具有一定的导向性,可为函数与几何问题的突破提供解法参考. 如上述从关键点入手,联系几何特性的思路不仅适用于初中的反比例函数与几何综合题,对后续高中数学的同类考题也具有参考价值,因此学生在学习中需要洞悉考题结构,总结方法思路,形成解题策略. 另外数形结合也是解析函数与几何类考题的常用方法,数形结合解析问题,即以形助数,以数辅形,是实现“数”与“形”有效融合的方法. 通过数形结合可以把握曲线图像与几何图形的结构及关联,打开问题的突破口,构建问题解析的思路.
总之,开展考题探究应关注问题的考查内容、解析思路和拓展方向,形成类型问题系统的知识与方法储备. 反比例函数与几何综合题是中考的典型问题,其问题结构和突破思路具有广泛适用性,教师要在教学中引导学生关注问题,总结方法,强化思维,稳步提升.
