融合信息技术教学 发展学生推理能力

汪元兴

[摘  要] 信息技术与学科融合已成趋势，教学设计应根据实际，融合现代信息技术整合教学内容，改进教学方法，提高实效. 文章以“三角形”的章起始课“认识三角形（第1课时）”的教学设计为例，阐述了如何融合信息技术，发展学生推理能力的一些做法与思考.

[关键词] 信息技术;融合;概念教学;推理能力

《义务教育数学课程标准（2011年版）》（以下简称《课标》）提出：“信息技术的发展对数学教育的价值、目标、内容以及教学方式产生了很大的影响.数学课程的设计与实施应根据实际情况合理地运用现代信息技术，要注意信息技术与课程内容的整合，注重实效.”《国家中长期教育改革和发展规划纲要（2010-2020年）》提出要“强化信息技术应用”，教师要更新教学观念，改进教学方法，提高教学效果.自2016年以来，“数学核心素养”开始备受关注，而“逻辑推理”就是六项关键能力之一. 现以北师大版七年级下册“认识三角形（第1课时）”的教学设计为例，谈谈如何融合现代信息技术，鼓励学生运用信息技术自主学习，发展学生逻辑推理能力的一些做法与思考.

基本情况分析

1. 教材分析

内容选自北师大版七年级下册数学教材第四章“三角形”的第一节“认识三角形（第一课时）”. 小学教材已出现“三角形”，但未正式定义;通过撕纸、测量等方法归纳出“三角形的三个内角和等于180°”.在七年级，本节课是“三角形”的起始课，将为后面学习三角形的三边关系、三角形的全等以及全等三角形的判定等打下基础. 因此，本节内容具有承上启下的作用.

2.学情分析

授课班级为数字平板走读班，课室配有一体机，学生人手一台平板，能够熟练地使用早上数字课堂系统，能够积极地参与数学学习活动.在小学学过三角形的一些初步知识，能在生活中抽象出三角形的几何图形;通过撕纸、测量等方法归纳出“三角形的内角和为180°”，具备了直观操作的经验. 在第二章，学生对两直线平行的条件以及平行线的特征进行了探索，具备了利用平行线的结论推导出“三角形的内角和为180°”这一结论的基础.

3. 教学目标

（1）通过观察、抽象，理解三角形的概念，了解直角三角形的概念;

（2）通过探索证明“三角形的内角和等于180°”，发展学生的逻辑推理能力;

（3）会按内角的大小对三角形进行分类.

4. 教学的重点与难点

重点：三角形的概念，探索证明“三角形的内角和等于180°”.

难点：探索证明“三角形的内角和等于180°”.

■ 教学过程

1. 环节一：情境引入

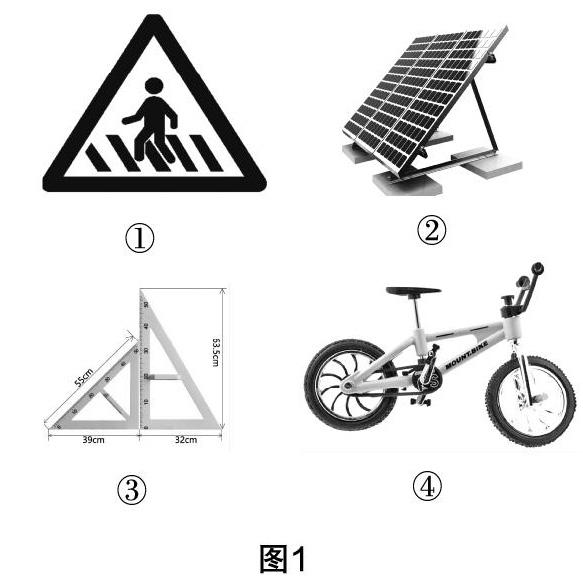
师：观察图1中的四幅图，相同的图形是什么？

教师活动：PPT展示生活中有关三角形的图片，引导学生观察，并另举实例，引出课题.

学生活动：观察图片，感受生活中的三角形.

设计说明  引导学生从生活实例中抽象出三角形图形，感受数学知识源于生活，激发学生学习数学的兴趣，同时为抽象出数学化的三角形作铺垫.

2. 环节二：展示目标（学习目标）

（1）理解三角形的概念及其基本要素：边、角、顶点，会用符号“△”表示三角形;

（2）探索并證明三角形的内角和定理（重点和难点）;

（3）会按角的大小对三角形进行分类，了解直角三角形的概念.

教师活动：通过早上课堂系统，同屏PPT内容，展示学习目标.

学生活动：阅读学习目标.

设计说明  同屏展示学习目标，让学生明确本节课的学习任务.

3. 环节三：教师导学

问题：面对一个新的几何对象——三角形，我们该怎样研究它呢？“温故而知新”，我们可以从已有的学习经验中找到思路. （回顾上一学期“角”的学习，我们研究了角的哪些内容？是按怎样的路径展开研究的？PPT展示）

角的定义→角的表示→角的分类→角的性质（比较大小）.

下面，我们能不能尝试着按类似的途径对三角形展开研究呢？

设计说明  引导学生类比角的学习方法，尝试对三角形展开研究，进一步体会学习几何对象的一般套路.

【导学一：三角形的概念及其符号表示】

师：你能从图2中找出几个不同的三角形？这些三角形有什么共同特点？（说明：PPT先展示图2，再展示拆分的图2-1至图2-5，随后引导学生阅读课本P81，回答下列问题）

问题1：什么叫作三角形？其基本要素是：_____________.

问题2：图2-1的三角形可表示为：_____________.

问题3：图2-1的三角形的三条边可表示为：_____________.

（说明：图2-1为课本P81的图）

教师活动：通过早上课堂系统推送问题，观察学生作答情况，展示学生典型作答，引导学生细读教材，掌握学习几何概念的一般方法.

学生活动：先独立在平板上作答，再与同学交流，修正错误，规范书写符号.

设计说明  先让学生独立思考，再引导学生阅读课本第81页相关内容，在“问题1”中提示学生划出关键词句.根据章建跃博士有关概念教学的理论，引导学生结合生活中三角形的图例，去掉物理属性，抽象出纯粹三角形图形的一般特征（有三个顶点、三条边、三个角），进而获得三角形的概念. 重点突出“不在同一直线上”“首尾顺次相接”，为后面理解三角形的三边关系及其他性质打好基础.在“问题2”强调用符号表示三角形时要简明、准确，规定要用“△+大写字母”;在“问题3”直接说明边的表示可用两个大写字母（如BC），也可以用一个小写字母（如边BC也可表示为a）.

【导学二：探索和证明三角形的内角和定理】

（1）小學时你是如何得到三角形三个内角的和是180°的？

（2）阅读课本第82页“做一做”，你能理解小明的思路吗？尝试把证明过程写出来.

（3）交流展示. （用希沃授课助手投影学生的推理过程）

（4）归纳结论：三角形三个内角的和等于180°.

教师活动：出示问题，观察学生课堂实际表现，适时给予引导，包括明确推理的必要性、如何由“180°”想到“引平行线”、如何规范书写推理过程等.

学生活动：按老师要求独立思考后小组交流展示.

设计说明  回顾在小学时探索“三角形的内角和等于180°”的方法，感受归纳推理;同时指出撕纸、测量会有误差，需要更为严谨的逻辑推理.通过提示由“180°”，想到“互补”“平角”等，引发学生思考如何用数学的方法移动角，将三个角集中到三角形的某一个顶点，能否利用平行线的有关性质说明这个结论，进而引导学生想到“引平行线”的方法.这一环节，先让学生独立思考，再交流展示.通过希沃授课助手投影学生的推理过程，或者利用早上系统同屏展示不同解答，及时暴露学生可能存在的问题，经师生评议修正，深化理解;学生可以截屏笔记，省时高效.这样做能够将直观感知和逻辑推理结合，由直观思维过渡到抽象思维，更好地发展学生的逻辑推理能力.

【检测1】

（1）在△ABC中，∠A=80°，∠B=∠C，则∠C=（？摇？摇    ）

A. 80°

B. 50°

C. 60°

D. 不确定

（2）已知△ABC中，∠A ∶ ∠B ∶ ∠C=2 ∶ 3 ∶ 4，求∠A，∠C的度数.

（3）阅读课本第82页“议一议”，回答相关问题.

（4）图3①中小明所拿三角形被遮住的两个内角是什么角？小颖的呢？

图3②中三角形被遮住的两个内角可能是什么角？将结果与图3①进行比较.

教师活动：推送问题，观察学生的掌握情况，评讲议一议图3②后，板书“分类讨论”.

学生活动：按要求作答，口述解题思路.

设计说明  巩固练习，加深理解.在议一议图3②中渗透分类讨论思想.

【导学三：按内角的大小把三角形分类】

教师活动：平板推送，同屏投影，板书“Rt△ABC”，要求学生做笔记（可截屏）.

学生活动：同屏阅读，按要求做笔记.

设计说明  先让学生阅读课本，再同屏投影，引导学生做笔记，明晰三角形按角的大小分为三类，同时突出直角三角形的符号表示和直角三角形两锐角互余的结论.

【检测2】

（1）观察图5中的三角形，并把它们的标号填入相应的方框内.

（2）一个三角形两个内角的度数分别如下，这个三角形是什么三角形？

①30°和 60°;

②40°和 70°;

③50°和 20°.

（3）在直角三角形中，有一锐角是另一个锐角的2倍，求这个锐角的度数.

教师活动：出示问题，观察学生的作答情况，展示并引导学生评议第3题的作答情况.

学生活动：回答问题，展示第3题的解答过程，全班评议，规范解答格式.

设计说明  检测三角形按角分类，及直角三角形两锐互余这一性质.利用早上课堂系统的同屏对比功能，重点展示学生对第3题的不同解法（预设学生可能会设“这个锐角为x度”，也可能会设“另一个锐角为x度”），优化课堂教学，提升课堂教学效率.

4. 环节四：课堂小结

问题1：这节课学习了什么内容？

问题2：我们是如何探索和说明三角形内角和为180°的？

问题3：对于今天的学习，你还有什么疑问？

问题4：类比角的研究过程，下节课我们将学习三角形的什么内容呢？

教师活动：口头引导学生回顾本课所学内容，同屏投影主体内容.

学生活动：口头小结，截屏做笔记.

设计说明  以反思性问题（如问题2）提升课堂小结的思维层次.先让学生口述，再同屏投影，让学生截屏做笔记，突出本节课主体内容.

5. 环节五：课堂检测 （早上课堂系统在线考试）

（1）已知△ABC中，∠A=70°，∠B=60°，则∠C=（     ？）

A. 50°     B. 60°     C. 70°     D. 80°

（2）若一个三角形三个内角度数的比为1 ∶ 3 ∶ 5，则这个三角形是（     ？）

A. 直角三角形      B. 锐角三角形

C. 钝角三角形     D. 无法确定

（3）直角三角形中，有一个锐角是另一个锐角的4倍，则这个直角三角形中一个锐角的度数是（      ）

A. 9°     B. 18°     C. 27°     D. 36°

（4）如图6，在△ABC中，∠C=60°，沿图中虚线截去∠C，则∠1+∠2等于（   ）

A. 120°         B. 180°

C. 240°        D. 260°

（5）如图7，在△ABC中，∠ABC，∠ACB的平分线BE，CD相交于点F，∠ABC=30°， ∠A=70°，则∠BFC等于（     ？）

A. 100°              B. 110°

C. 115°              D. 125°

教师活动：早上课堂系统在线考试;根据系统自动生成的数据分析，进行针对性讲评.

学生活动：在线测试，独立完成后交流展示，重点展示解题方法，评议错题.

设计说明  利用早上课堂系统，实施课堂在线测试，根据系统生成的成绩数据统计分析，实时反馈全班学生的作答情况，对正确率低于80%的题目进行针对性讲评. 这里设置了有梯度的检测题，满足不同层次学生的学习需要，要求学生独立完成后再交流，口述解题思路，进一步发展学生的逻辑推理能力.

附：课堂考试成绩分析统计图（部分）（见图8）.

■ 教学反思

课后，笔者对信息技术融合下的数学课堂进行了反思.（1）融合信息技术，有利于充实教学内容，发展学生推理能力.教材以观察木屋顶框架图导入，考虑到较多学生可能不熟悉，在教学设计时，补充了部分生活中的三角形图片，充实了内容，有助于学生通过生活图例，抽象出具体的三角形图形，進而理解三角形的概念.考虑到学生数学基础较好，在学习第二章“相交线与平行线”时，对逻辑推理有了较为严谨的书写格式，所以借助一体机、学生平板，结合几何画板和在线测试等，充实了教学内容，丰富了学生的学习方式.结合“由180°，想到什么”，比较自然地引发学生思考，如何通过“引平行线”，结合平行线的性质证明三角形内角和定理，同时借助希沃授课助手同屏展示学生的作答情况，结合师生共同评议，指导学生有条理地表达推理过程，由归纳推理到逻辑推理，较好地发展了学生的逻辑推理能力. （2）传统的黑板板书不能丢. 虽然信息技术的发展，给课堂教学带来了很大便利，但要有选择地合理使用，同时要重视板书设计，结合教学内容，板演分析问题和解决问题的过程，帮助学生更好地理解相关知识. （3）类比角的研究过程，展开对三角形的研究学习，有利于引导学生进一步体验研究几何对象的一般思路，为以后继续类比学习其他几何对象打好基础，不断加深对几何推理论证的认识.