分层走班模式下 数学基础层课堂教学基本策略探析
2020-11-06叶新和
[摘 要] 分层走班体现了“以生为本”的教育思想. 实验中,将学生分为基础层、发展层、提高层. “基于基础层,依靠基础层”是分层走班模式下数学基础层的基本教学策略. “基于基础层”,首先要了解基础层的学生,其次要针对基础层进行教学设计;“依靠基础层”,主要指依靠学生自我,其次依靠其他学生进行学习.
[关键词] 分层走班;基础层;教学策略
关于数学学科分层走班的教学改革实验,泰州市许庄初中数学备课组从2014年春学期开始正式实施,先后成为泰州市微创新优秀案例、泰州市基础教育改革前瞻性项目[1],申报的江苏省“十二五”规划重点课题已进入结题阶段,市内外多家学校先后来观摩学习. 2019年春学期,九年级的数学、物理、化学三门学科同时实施分层走班实验. 2019年秋学期,新的九年级的数学和物理实施分层走班实验. 2019年12月,教学改革模式入选“江苏初中课堂教学改革优秀成果”(由江苏教育报刊总社、江苏教育学会初中专委会共同评审).
实验中,根据学生的数学综合基础(数学成绩、非智力因素的综合),结合学生及其家长的意愿,将学生分为基础层、发展层和提高层三个层级,在数学课堂学习时,同一层级的学生分别从行政班走到同一个班级学习[1]. 在工作变动前,笔者一直担任数学学科基础层的教学工作,并进行了一些探索与思考. 2017年9月,高港电视台在《党员先锋谱》栏目中对笔者进行报道时,就基础层的学习成效专门进行了介绍.
在探讨农村初中数学学科分层走班的必要性时,笔者指出,决定农村初中学科分层走班的理论依据是最近发展区理论,事实依据是农村初中学生在数学学科方面的差异比较大[1]. 表面来看,分层走班仅仅是在教学组织形式方面进行了变化,但实际上它关注了学生的差异化,反映了教师“以生为本”的教育思想,体现了因材施教的教学原则. “以生为本”教育思想的核心是基于学生、依靠学生、为了学生,其中的“为了学生”主要指价值指向,因而“基于基础层,依靠基础层”就应当成为分层走班模式下数学基础层的基本教学策略.
■ 基于基础层
基于基础层,是精准教学的前提. 基于基础层,首先要了解基础层的学生,其次要针对基础层进行教学设计.
1. 了解基础层的学生
(1)要了解基础层的学生的非智力因素情况
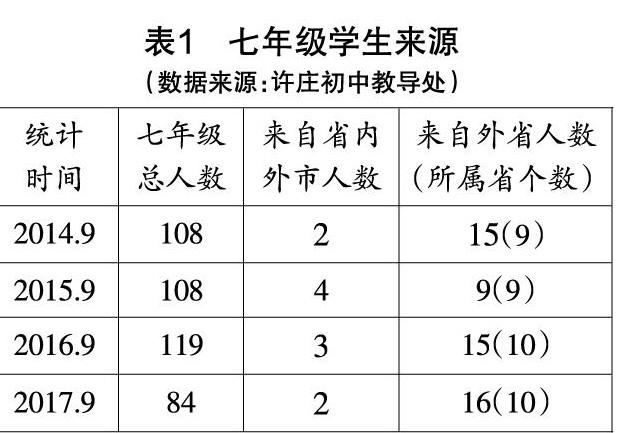
表1为近几年许庄初中七年级学生的来源,从表格中可以看出,许庄初中外来务工子女分布情况比较复杂,来自外省的学生数比例较高,每年涉及的省份通常为9~10个. 由于外来务工子女使用的数学教材往往不一样,学习态度、学习习惯通常也不好[1],对数学学科的兴趣往往也不浓厚,这些学生大多集中在基础层,因此了解他们的非智力因素情况应该是了解基础层学生的前提.
2015年,八年级基础层学生解答一道关于扇形统计图识别的练习题时,不少学生解答如下:2000×36%=620;2000×22%=460;2000×31%=640;2000×23%=480. 先不谈他们对题目的理解是否正确,这些低级计算错误更多地反映了学习态度.
(2)要了解基础层的学生的知识基础,尤其是知识缺陷
数学学习是一个循序渐进的过程,不少时候,新学的知识会了,但由于以前所学知识欠缺、基本技能没有掌握,所以新学的知识仍然不能正确解答. 比如计算1■-2■,根据减法法则容易得到1■+-2■,如果不会异号两数相加或者不会通分,便不能得到正确的答案,为此,需要先了解他们的相关知识是否具备,如果没有具备,就要进行一定的弥补.
(3)要了解基础层的学生的思维方式
基础层学生的思维方式有时可能是与众不同的. 比如根据8>6,从而认为■>■;再如,计算■+■时,将分子、分母当成独立的数字来求和,得出答案■. 这些都是在整数推理不适用的情况下继续运用它■[2]. 可见,只有了解基础层学生的思维方式,才能进行针对性的教学,教学的有效性才能得到提高.
2. 针对基础层进行教学设计
(1)考虑对知识缺陷处进行弥补
课前,教师可针对学习新知所需的知识、技能设置2~4道预备性的试题,以了解他们的知识掌握情况. 普遍存在的问題,如果通过简单提醒可以解决,那么课堂上教师应及时“带一带”,比如解简单的分式方程时,教师就可以及时带一带解含括号整式方程的方法以及提醒一下去括号时的注意点;如果通过简单提醒不能解决,那么可以在教授新的学习内容前先集中补救.
(2)注意对易错的重要内容进行引导,从多个角度来认识
比如“若关于x的方程■=1的解是正数,则a的取值范围是______”,学生容易遗漏限制条件“a≠-2”. 为此,可从以下角度来认识:①从前提条件的角度来认识. 等号左边的分式有意义,方程才存在,才谈得上“解是正数”,所以分母x-1≠0. ②从隐含条件角度来认识. “方程的解是正数”隐含了“方程有解”,即x=-1-a不是增根,所以-1-a-1≠0. ③从分式运算的角度来验证. 若a=-2,则只要分式■有意义,它的值总是2. 由于2≠1,此时方程无解,因此a≠-2[3]■.
学生的解答出现错误,不少时候是解答中的一两步出现错误,有时是思路不够严谨,理由不够充分,有时是忽视前提条件、隐含条件、限制条件. 此处,可将学生易犯的错误作为重要教学资源进行处理,从多个角度共同分析,让他们明白错在何处,为什么错,以及如何纠正,用较少的时间来提升学生的理解能力,同时增强他们对错误的免疫力. 更重要的是,通过分析与改进的示范,学生树立了“错误不可怕,错误能改正”的信心.
(3)对于典型例题,问题通常要适当铺垫
对于基础层的学生来说,他们有的基础知识欠缺,有的思维能力跟不上,有的注意时间不长,有的记忆长度不够,学习时同化与顺应的速度相对比较慢,因此对于典型例题,问题拾级而上、课堂学习节奏推进得适当慢一些,便显得很有必要. 比如对于试题“比较 2100与375的大小”,事先可进行如下铺垫:①比较16与27 的大小;②比较1625与2725的大小. 在此基础上再来看最初的问题,学生便容易理解与接受. 对于典型例题,还可以做适度变式与延伸,引导学生在变化中发现规律、揭示题目本质,从而提高思维能力.
进行针对性教学设计,要注意适时降低部分内容的学习要求. 一方面是时间限制. 前述做法都需要额外的时间,然而分层走班时学习时间固定且有限. 另一方面是调整教学内容的教学要求,使之更贴近基础层学生的最近发展区,从而提升学习效率.
■ 依靠基础层
学生是学习的主人,基础层的学生也应该如此. 只不过,基础层的学生在以往学习中经常感受到的是失败的体验,慢慢地便产生了挫败感与无助感,有的时候甚至会自暴自弃. 在分层走班模式下,依靠学生自我来激发学生的学习内驱力是提高教学有效性的关键,也应该成为教学的根本举措.
1. 依靠学生的动手实践形成经验
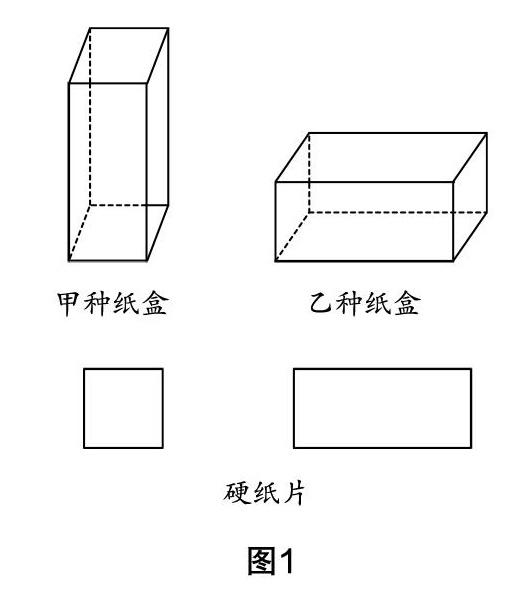
比如问题:如图1,要制作甲、乙两种无盖的长方体纸盒,需用正方形和长方形两种硬纸片,且长方形硬纸片的宽与正方形硬纸片的边长相等. 现有150张正方形硬纸片和300张长方形硬纸片,可制作甲、乙两种纸盒各多少个[4]?
从教科书提供的图形来看,每种纸盒所需要的两种硬纸片的个数不够明显. 教学中,笔者让基础层的学生按照要求事先准备一些长方形硬纸片和正方形硬纸片,并糊成甲、乙两种纸盒各一个,课上观察每种纸盒分别需要长方形硬纸片和正方形硬纸片各几张,在观察中感知数量关系. 接着指出,考试中无法糊纸盒又该如何寻找数量关系呢?引导学生发现可以采用涂色的方法来加以区分,即在纸上将纸盒无盖面用铅笔涂色,再寻找数量关系:一个甲种纸盒需要长方形硬纸片4张和正方形硬纸片1张;一个乙种纸盒需要长方形硬纸片3张和正方形硬纸片2张,从而逐步形成空间观念. 然后小组合作,比如用5张正方形硬纸片和10张长方形硬纸片试着糊纸盒,观察、体会两种纸盒中正方形硬纸片、长方形硬纸片的来源,发现其中的数量关系:①甲中正方形硬纸片的张数+乙中正方形硬纸片的张数=总的正方形硬纸片的张数,②甲中长方形硬纸片的张数+乙中长方形硬纸片的张数=总的长方形硬纸片的张数,再据此解决原先比较复杂的问题.
上述过程中的几次实践都很有必要:首先,在糊纸盒的基础上观察数量关系是提供学生亲身经历的机会,有了这样的经历,他们才会对其中的数量关系有明确的且印象深刻的认识;接着,对照实物,观察并体会“无盖”,感受有面与无面的区别,这样才容易想到用涂色的方法来区分是否有面,从而显示出硬纸片的张数;此后,小组合作试着糊纸盒,这样的实践对于观察、体会两种纸盒中正方形硬纸片和长方形硬纸片的来源也具有不可代替的作用,在此基础上容易发现复杂的数量关系,即150张正方形硬纸片和300张长方形硬纸片,与可制作的甲、乙两种纸盒个数之间的关系,至此,列出方程组已变得水到渠成.
2. 依靠学生的成功体验
一般来说,基础层的学生对数学学科的兴趣不浓或者没有兴趣,所以给予一定的激励能提高基础层学生的学习积极性. 不过,能真正使学生长时间保持浓厚兴趣的是通过学习掌握相应的学习内容,从而获得成就感. 基于这样的角度,再看前面的针对性教学设计,及时弥补知识缺陷处、适当铺垫与变式、适当降低要求等做法也显得颇为必要.
3. 依靠学生的自我反思来促进“生长”
相对其他层次的学生来说,基础层的学生更不会反思. 为此,教师首先要通过具体的例子,站在学生的角度来展示如何进行反思;其次,要做一个有心人,适时“留白”,给他们反思的时间与空间.
比如,对于这道题“无论a取什么实数,点A(2a,4a+1)都在直线l上,则直线l的解析式是______(高港区2017年秋学期八年级数学期末调研测试题)”,教学中教师进行引导:(1)要确定一条直线,需要找直线上的几个点?(2)“无论a取什么实数”都可以,意味着什么?a取简单的数值,比如0,1可以吗?(3)此时,得到的点(0,1),(2,5)能确定一条直线吗?如何求直线的解析式?在此基础上,引导学生回顾:题目中指出“无论a取什么实数”,那么前面的a仅仅取0,1两个数值,解决办法是否严密?此为第一次反思,得到“解法逻辑不够严谨,需要改进”的结论. 那么,如何说明“无论a取什么实数,点A(2a,4a+1)都在一次函数y=2x+1的图像上”呢?可以将(2a,4a+1)代入解析式y=2x+1,验证是否成立,从而得到逻辑严谨的解法. 再看“通过解方程组求直线解析式”的解法,感觉解答过程比较烦琐,那么有没有简便的方法呢?此为第二次反思. 可以抓住验证内容y=2×(2a)+1=4a+1做文章:逆之可得y=4a+1=2×(2a)+1,对此有两种理解,一是令x=2a,从而4a=2x,所以有y=2x+1;二是由x=2a解得a=■,代入y=4a+1中消去a,也得y=2x+1. 从上述处理与反思的过程中,你又有何启迪?此为第三次反思. 本题并不容易,按照上述方式来处理,基础层的学生也能比较好地理解,且通过三次不同层次的反思实践,能让他们慢慢地对如何反思有所认识与感受,从而慢慢地学会反思.
依靠学生,除了要依靠学生自我之外,还应重视依靠其他学生. 前面制作纸盒的应用题教学中已有所体现,限于篇幅,不再赘述.
参考文献:
[1]叶新和. 分层走班必要性探析——以泰州市许庄初中为例[J]. 泰州教育,2018(6).
[2](美)多诺万,(美)布兰思福特主编;史亚娟译. 学生是如何学习的:课堂中的数学[M]. 南宁:广西师范大学出版社,2011.
[3]葉新和. 数学章节复习的有效探索[J]. 教学与管理,2013(4).
[4] 杨裕前,董林伟. 义务教育教科书数学七年级下册[M]. 南京:江苏凤凰科学技术出版社,2013.
