浅谈学生问题意识的培养策略

2020-11-06沈娟

数学教学通讯·初中版 2020年9期

沈娟

[摘要] 如何培养学生问题意识，让学生形成主动探究和自然提出问题的习惯，成为所有数学教师思考的问题. 文章结合多个案例，说明培养问题意识的路径：创设问题情境，使学生想问;保护好奇心理，使学生敢问;适当变式训练，使学生会问;聚焦方法指导，使学生善问.

[关键词] 提出问题;问题意识;培养

伴随着时代的不断发展，以创新思维为核心的自主创新能力得到了充分的关注，问题意识得到了广泛的重视. 学生提出问题的能力不是靠传授而得到的，它是学习者经过“脑风暴”后的顿悟而形成的. 因而，培养学生的问题意识必须依靠潜移默化的熏陶，让学生形成主动探究的习惯，进而自然提出问题. 笔者结合新一轮基础课程改革的目标，基于学生问题意识的培养，进行了多次大胆的实践尝试，取得了较好的效果. 现将实践尝试的过程和一点思考进行整理，与同仁交流.

創设问题情境，使学生想问

不少专家从辩证唯物主义认识论、数学文化以及现代数学观等视角对“数学情境与提出问题”进行了多元化的论述，指出了实施的原则、策略以及取得的成果. 由此可见，问题情境对学生问题意识的培养意义重大. 因此，教师需从学生的认知水平、教学内容出发，有意识、有目的地创设问题情境，动摇学生已有知识结构的平衡状态，使其产生疑惑，使他们想问，从而使整个教学过程充满问题、充满互动.

案例1 一元二次方程

师：基于你们自身对一元二次方程概念的理解和定位，试着写出一个一元二次方程.

（这是学生感兴趣的数学活动，自然各个跃跃欲试，呈现多样化展示的精彩场面）

教师选择部分方程进行展示：①x2-5=0;②x2-2x-3=0;③■x2-4x-1=0;④x2-■x+4=0;⑤ax2+bx+c=0.

师：大家一起观察你们所写的方程，能否进行针对性的提问？

生1：请试着求解以上一元二次方程.

生2：不对，应先判断以上方程是否都是一元二次方程. 比如上述方程中的“⑤ax2+bx+c=0”，当a=0，b≠0时，该方程则为一元一次方程.

生3：是否可以不解方程求出以上每个一元二次方程两根的平方和.

生4：不对，首先需判断其是否有实根，若有，请求出方程两根的平方和.

……

师：你们的提问都非常精彩，那老师也提一个问题. 谁能列举一个含有字母的一元二次方程？

生5：这个简单，（m-1）x2+2x+3=0.

生6：不对，该方程并非一定是一元二次方程. 你看，当m=1时，方程为2x+3=0，所以，只有当m≠1时，方程（m-1）·x2+2x+3=0才是一元二次方程.

生7：我认为还不够完善，只有当m为不等于1的常数时，（m-1）x2+2x+3=0才是一元二次方程.

……

以上案例中，教师的课堂处理简明而直接，教师的问题情境精巧而合理，自然诱发学生的问题意识，通过交流不同的思路，使其不断地提出问题，彰显了学生的数学能力.

保护好奇心理，使学生敢问

学生由于受到自身知识水平和理解能力的影响，提出问题的能力是有差异的，一些学生提出的问题具有较高的层次性，而有些学生的问题不切主题，甚至会有些可笑. 对于教师来说，除了以睿智激起学生提出问题的欲望，还需保护学生的好奇心理，尊重学生提出的问题，以鼓励的言语和激励的眼神去开启学生的心智，让学生敞开心扉，敢于提问，展现自己的个性.

案例2 三角形的三边关系

师：经过刚才的探讨，你们能提出哪些问题？

生1：满足什么条件的才是直角三角形？

师：这个问题很不错，那你是否可以解答呢？

生1：当三角形的三边a，b，c满足a2+b2=c2时，这个三角形即为直角三角形.

师：那三边长a，b，c有何要求吗？

生1：没有，是任意的.

师：真的吗？那我们一起试着摆一摆，看看生1的结论是不是正确呢？

（学生兴致勃勃地投入操作）

生2：生1的判断是错误的，三角形的三边并非任意的.

师：那如何判断三条线段是不是可以组成一个三角形呢？

（学生展开了讨论，并对操作所得的数据进行深入分析，有了新的认识）

生3：只有任意两条边的和大于第三条边，任意两条边的差小于第三边才能组成一个三角形.

上述案例中，教师创造机会让学生去提问，但却不解决学生针对情境所提出的问题，而是留下悬念，让学生去思考、去探究、去讨论、去质疑，让新知真正在学生的知识体系中扎根和生长，促进学生对数学知识的深刻理解[1].

适当变式训练，使学生会问

问题是产生学习动机的载体，问题是诱发和激起求知欲的根本. 学生感知不到问题的存在，就无法真正深入思考，这样的学习也将是浅层的;而一旦学生有了问题意识，学习才是深刻的、有效的. “授人以鱼不如授人以渔”，我们可以以适当的变式训练，引导学生比较新旧知识间的异同点而发问，再让学生进行发散性思维，尝试进行适当的变式，以训练学生的问题意识和数学思维.

案例3 让学生尝试提问

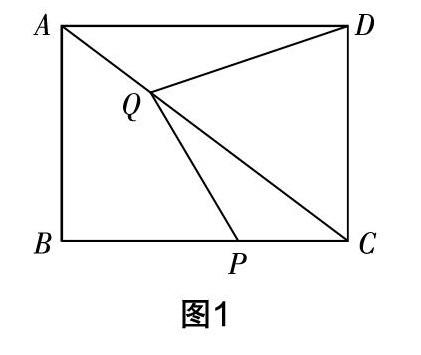
如图1，已知矩形ABCD中，有AB=6，BC=8，且动点P从点C开始以1个单位每秒的速度，在CB上向着点B运动. 同时，动点Q以与动点P相同的速度从A点开始在AC上向着点C运动. 连接PQ，DQ，设时间为t.

生1：这是一道题目吗？它在问什么啊？

生2：这道题目为什么没有求解或者证明？

（教师一直微笑地看着学生，学生则一直处于困惑中）

师：爱因斯坦曾说，提出一个问题远比解决一个问题更加重要. 而我们一直在解决问题，很少提出问题，那你们是否可以根据以上材料提出一个数学问题呢？我们可以从简单的问题开始尝试.

（学生思考和讨论）

经过五分钟左右的思考和探讨后，学生开始提问.

生3：试求出AC的长.

生4：请试着用t来表示AQ和CP的长.

生5：当t为何值时，PQ//AB.

生6：当t为何值时，CP=PQ.

生7：试求出线段QD的最小值.

生8：当t为何值时，△CPQ为等腰三角形.

生9：当t为何值时，△ADQ为等腰三角形.

生10：当t为何值时，△CPQ为直角三角形.

生11：试求出四边形ABPQ面积的最值.

……

以上案例中，教师问题的设计具有很大的开放性，由于已经到达初中的复习阶段，所以学生提问的深度和广度较大，涉及的图形和知识也会很多. 学生在思考如何提问、提出什么问题和从哪个方面提问的时候，会充分调动自身已有知识经验，从而达到本节课的学习目的. 在学生思考并提出问题的过程中，教师可以适时点拨和引导，尽量让学生的问题既具有多样化的特征，又具有一定的探究意义[2].

聚焦方法指导，使学生善问

马赫穆托夫在他的“问题教学”理论里提出，问题的提出主要分为以下三个阶段：第一阶段：分析问题情境;第二阶段：“看出”问题实质;第三阶段：通过语言来概述问题. 由此可见，提出问题也是“有法可依”的. 因此，为了更好地培养问题意识，教师需聚焦方法指导，潜移默化地教给学生提出问题的方法，使学生勇于提问又善于提问，使我们的课堂交流深入而高效，使学生提出问题能力的培养落到实处.

案例4 相似三角形的判定

师：相似三角形的一种特殊情况是什么？

生1：是全等三角形.

师：很好. 那全等三角形的判定有几种方法？

生2：有SSS，SAS，ASA和AAS这4种方法.

师：很好，那么据此你可以提出哪些问题呢？下面請分组讨论.

（学生投入讨论，片刻后有了结果）

生3：若两个三角形的两个角对应相等且一组对应边之比相等，那么它们相似吗？

生4：不对吧，一组对应边之比好像并不存在与谁相等的问题.

师：那这个问题该如何修正呢？

生4：若两个三角形的两角对应相等，那么它们相似吗？

师：还有其他问题吗？