野渡无人舟自横现象的数值研究

余勇飞 陈 沉 斯铁冬 胡 婷 魏家望

(中国电建集团华东勘测设计研究院有限公司，杭州311100)

(浙江华东工程数字技术有限公司，杭州311100)

“春潮带雨晚来急，野渡无人舟自横”。这首优美的诗句出自唐朝诗人韦应物之手，描绘的是傍晚荒郊野外的渡口，被拴住的一艘小船横于水面随波荡漾的美景。诗人所描绘的生动画面不仅给后人留下无穷无尽的遐想，同时诗中所阐述的力学现象也吸引了许多力学专家的注意[1]，并争相从不同专业角度来证明“野渡无人舟自横”这一力学现象。其中天津大学王振东[2-3]以流体力学观点将小船简化成一椭圆柱，并借助平面流动中复变函数理论，推导出椭圆柱在不可压缩流体中所受力矩公式，得出小船横于水流是稳定的平衡位置，而顺于水流是非稳定的平衡位置；之后，王振东等[4]又在实验室水槽中对这一力学现象进行了实验研究，同样得出小船横于水流是稳定的平衡位置，而顺于水流是非稳定的平衡位置这一结论，并证明该结论并不受水流速度等其他因素的影响；此外，周道祥[5]从流体力学伯努利原理出发，同样分析出了“野渡无人舟自横”这一力学实质，并将该理论成功应用于足球界“香蕉球”的分析计算。

以上诗人所描述以及学者所研究的物理现象可归结为物体在力作用下的平衡问题。本文将采用数值模拟手段对这一力学现象进行研究分析。

1 理论基础

站在流体力学角度，可以把“野渡无人舟自横”这一力学现象简化成椭圆在不可压缩流体中的二维流动。王振东教授根据绕流理论，推导出椭圆在流体中受到的合力矩M为

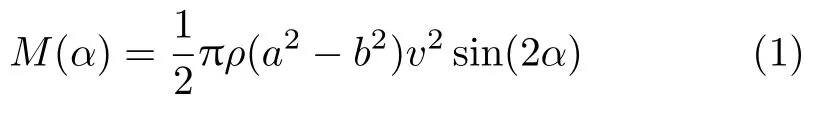
式中，ρ为流体密度，a为椭圆长半轴，b为椭圆短半轴，v为流体速度，α为椭圆长轴与来流速度夹角，如图1 所示。

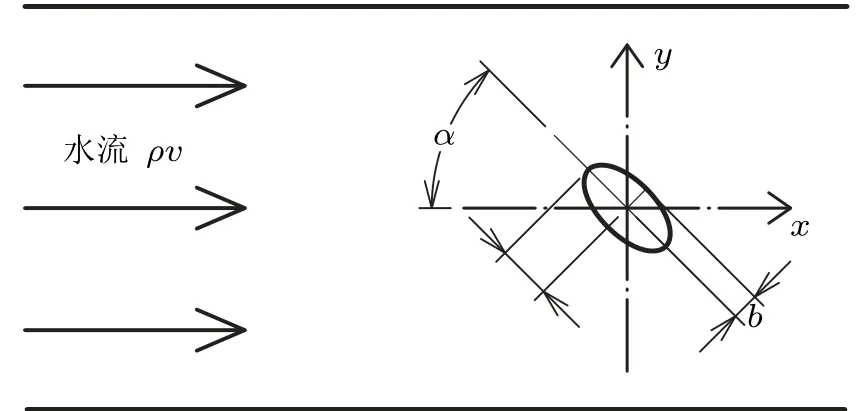
图1 物理模型

基于式(1)，王振东教授分析得出：小船横于水流是稳定的平衡位置，而顺于水流是非稳定的平衡位置的结论[2]。即无论小船初始位置在何处，在受到外力作用后发生偏转，最终都能在横于水流的位置重新建立起平衡。

本文将模拟小船在水流作用下，初始偏转角α=0，π/4 两种情况下的运动特性，以研究这一力学物理现象并验证以上理论分析的准确性。

2 数值模拟

根据刚体定轴转动定律，小船所受力矩M与转动角加速度之间的关系为

式中，I为小船转动惯量，对绕自身几何中心转动的二维椭圆柱小船，其转动惯量为I=m(a2+b2)/4；为小船转动时的瞬时角加速度。

通过对流场的仿真计算，可以获得小船周围的压力、速度场分布，从而计算出小船在任意偏转角α下所受到的合力矩M(α)。将M(α)代入式(2)进而求得小船瞬时角加速度。借助数值模拟中流固耦合技术，将设置给小船，便能模拟出小船在水流作用下绕几何中心的转动过程，同时还能获得小船α和M(α) 等物理量随时间的变化曲线。

2.1 模型建立及网格划分

对照王振东教授的“野渡无人舟自横” 水槽实验[4]，本文将小船假设为长半轴a= 5 cm，短半轴b= 2.5 cm 的椭圆，计算域取20a×8a，如图2所示。

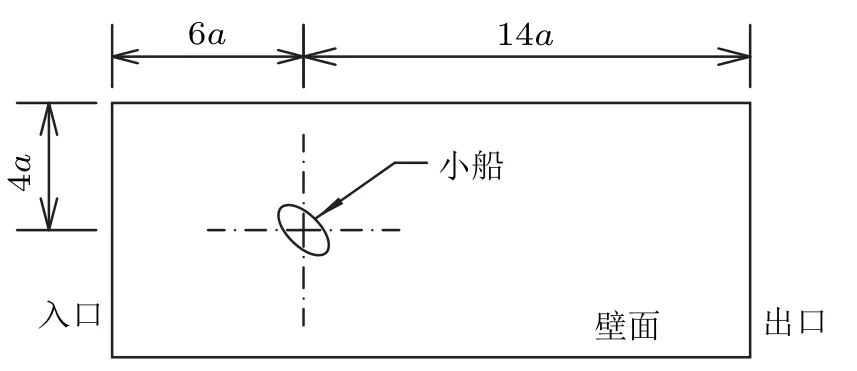
图2 模型计算区域

在建立模型网格时，考虑到小船周围流动的复杂性，对距小船中心半径4a范围内的网格进行了加密处理。整个计算域全部采用质量较高的结构化网格，节点数约为23 320 个，如图3 所示。

图3 计算区域网格

2.2 数值计算方法

湍流模型为标准k–e模型；采用SIMPLE 算法求解压力速度耦合方程；上下壁面采用无滑移条件；来流采用速度入口，出口为压力出口；压力离散格式采用二阶形式，动量方程离散格式采用二阶迎风格式。来流速度v取0.3 m/s，时间步长取0.002 s。

3 结果分析

3.1 运动状态分析

图4 为小船初始偏转角α= 0，π/4 两种状态下，计算得到的时间−偏转角曲线图。从图中可以得出：无论初始偏转角为何种状态，小船在受到外界扰动后都偏离了原位置。并且都围绕α= π/2 做阻尼振动，大约经过60 s 时间的调整后波动消失，随后小船在α=π/2 位置重新建立起了平衡状态。

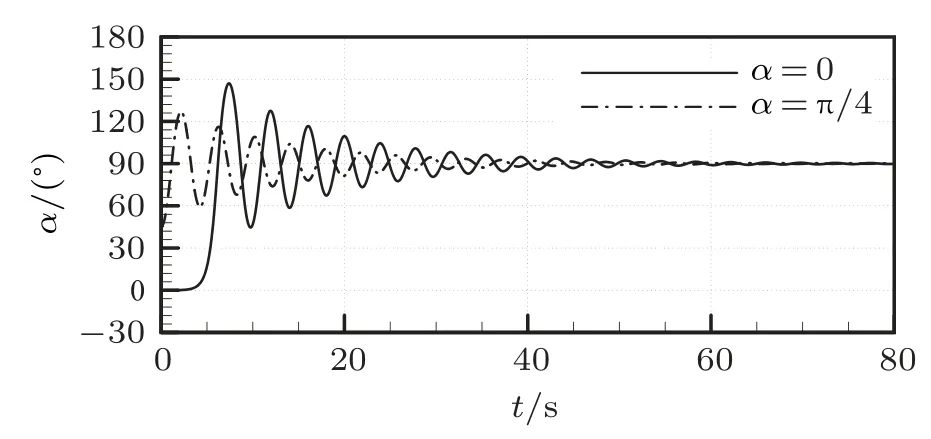
图4 时间与偏转角曲线

这一结果表明，无论小船最初偏转角α为何值，受外力作用发生偏转后，最终都能在横于水流的位置重新建立起平衡。

3.2 受力分析

图5 为小船初始偏转角α= 0，π/4 两种状态下，计算得到的时间与力矩曲线图。结合图4 分析得出，小船受到外界扰动发生偏转后，所受力矩M围绕M=0 做阻尼振动，大约经历60 s 时间的调整后波动消失，此时力矩M= 0。这表明小船最终将横于水面，并处于受力平衡的稳定状态。

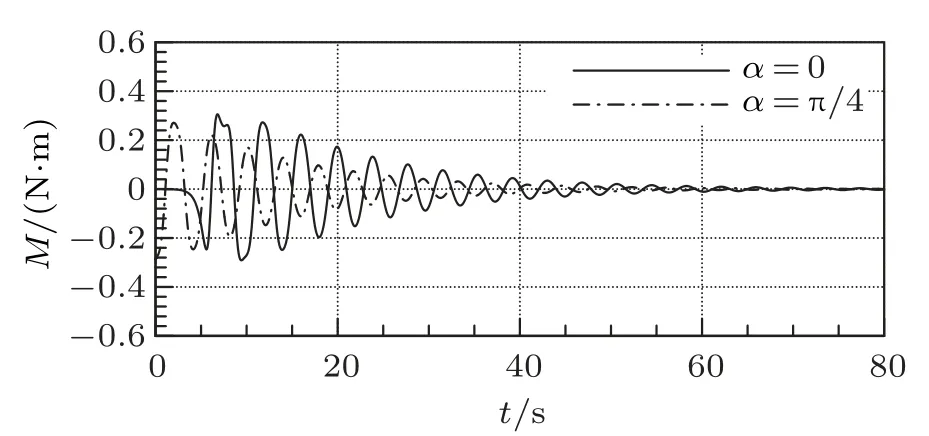
图5 时间与力矩曲线

综合上一节结论，可以得出：小船横于水流是稳定的平衡状态，即小船受到外力发生偏转后，最终都能在横于水流的位置重新建立起稳定的平衡。这一实验结果刚好与理论分析相吻合。

3.3 稳定性分析

上文通过对小船的运动状态以及受力状态进行分析，得出小船横于水流处于稳定平衡状态的结论，下文将进一步分析小船横于水流能处于稳定平衡状态的原因。

图6 为初始偏转角α= 0 方案，小船在发生偏转后20 s 内偏转角α以及力矩M时程变化曲线。横坐标为时间，左侧纵坐标为偏转角度α，右侧纵坐标为力矩M。实线为小船发生偏转角度α，虚线为小船受到的力矩M。

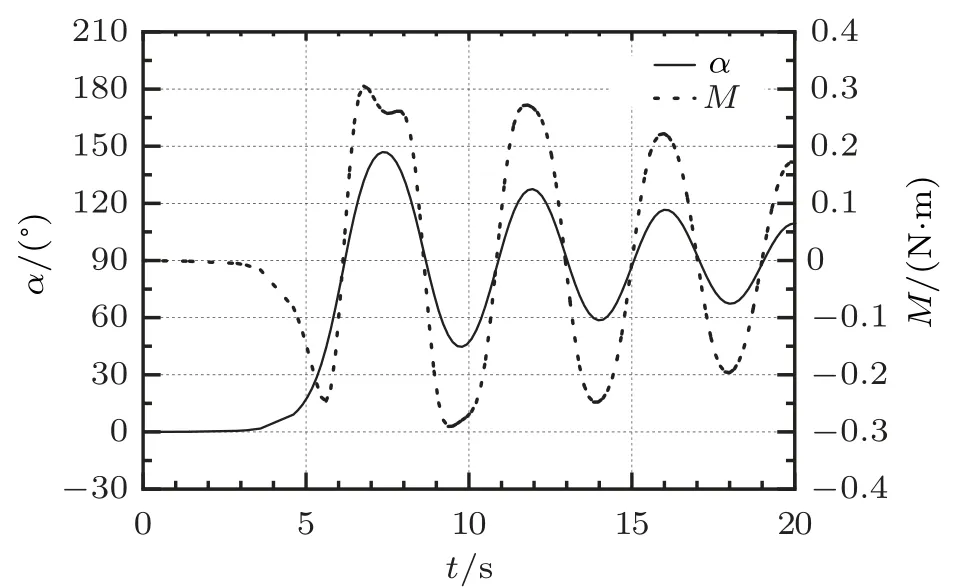
图6 偏转角与力矩局部时程变化

由图6 可以看出，当α= 0 或者α= π/2 时，小船受力矩M= 0，即小船顺于水流以及横于水流受力平衡。

在t= 0 s 时刻，小船顺于水流受力平衡。小船在受到扰动后沿顺时针方向发生偏转，与此同时产生一个同为顺时针方向的力矩M，该力矩将会使偏角α进一步增大，可见顺于水流这个平衡位置不稳定。

在t ≈6.5 s 附近，小船接近横于水流。由图可以看出：小船在横于水流附近，其偏转方向始终与所受力矩方向相反，即该力矩将阻碍小船的偏转，可见横于水流这个位置是稳定的。

观察图6 还发现：当偏转角α达到波峰或者波谷时，力矩M也基本处在波峰或者波谷位置，但第一个t −M波峰明显与其他时刻的波峰不同，猜测该异常可能是船身周边水流出现流动分离形成旋涡造成的。然而查看该时刻小船附近的流线分布，如图7 所示，发现船身周围并未出现流动分离现象，因此排除流动分离造成异常波峰的可能。

图7 t=7.5 s 小船周围流线分布

究其原因主要是如下所述：由式(1) 知小船与水流成π/4 或3π/4 时，所受力矩最大。在图6中，t= 6.8 s 时，小船偏转角经过α= 3π/4 位置，此时力矩M达到峰值；之后小船偏转角α继续增大而受到的力矩M则逐渐减小；t=7.5 s 时，偏转角α达到峰值，随后偏转角α逐渐减小同时受到的力矩M逐渐增大；t=8.0 s 时，小船偏转角再次经过α=3π/4 位置，受到的力矩M再次达到峰值，随后逐渐减小。这便是造成第一个t −M波峰曲线与其他时刻波峰曲线不同的原因。这一现象也从侧面证实式(1) 的正确性。

4 结论

本文采用数值模拟手段对“野渡无人舟自横”这一力学现象进行了详细分析，研究了小船在水流作用下的运动特性，结果表明：

(1) 数值模拟重现了“野渡无人舟自横” 这一力学现象，仿真结果也与相关文献理论分析结果吻合。

(2)小船顺着水流以及横于水流所受到的作用力矩M=0，都属于平衡位置。

(3)小船顺着水流属于非稳定的平衡位置，此时小船受扰动发生偏转后所产生的力矩与偏转方向相同。小船在该同向力矩作用下将进一步发生偏转，并再也恢复不到原平衡位置。

(4)小船横于水流属于稳定平衡位置，此时小船受到扰动发生偏转后所产生的力矩与偏转方向是相反的。因此在该位置，即使小船失去平衡，但最终也能在该逆向力矩的作用下重新恢复到原平衡位置。