低约束试件断裂韧性测试方法研究进展1)

2020-10-28武旭帅健许葵

力学与实践 2020年5期

武旭帅健许葵

(中国石油大学(北京) 安全与海洋工程学院，北京102249)

断裂韧性是材料最重要的性能之一，准确测试材料的断裂韧性对确保油气管道安全运营具有重要意义。自20 世纪60 年代以来，国内外对断裂韧性测试方法进行了较为广泛的研究，各种断裂韧性试验方法得到了广泛发展，其中最常用的标准试件为紧凑拉伸(compact tension, CT) 试件和单边缺口弯曲(single edge notched bend, SENB) 试件。这些标准试件在裂纹尖端具有较高约束条件[1-3]，对于浅裂纹，由于裂纹尖端约束较小，使用标准CT 或SENB试样测量的断裂韧性通常过于保守。因此，适用于低约束条件下的断裂韧性测试方法应运而生[4]。

在石油和天然气行业中，通常采用单边缺口拉伸试件(single edge notched tension, SENT) 测量管线钢低约束状态下的断裂韧性。该方法在基于应变的设计、工程临界评估以及适用性评价中都得到了广泛应用，大大节省了管道设计和维护成本，促进了管道安全运营技术的发展[5-6]。挪威船级社、加拿大矿物与能源研究中心[7-8]、埃克森美孚[9]分别针对SENT 试件J 积分阻力曲线和裂纹尖端张开位移(crack tip opening displacement, CTOD)阻力曲线提出了三种具有代表性的测试方法，其中DNV 方法为多试样法，其余两种为单试样法。英国标准协会在2014 年12 月发布了首个SENT 试件测试标准BS 8571[10]。然而，BS 8571 主要是基于DNV-RPF108 提出的，因而具有一定的局限性；美国材料与试验协会开发的SENB 和CT 试样阻力曲线测试标准ASTM E1820[11]并不适用于SENT 试件；我国也尚未发布关于低约束SENT 试件断裂韧性的测试标准。

本文对现有SENT 试件测试方法进行归纳总结，分析低约束试件常用断裂韧性表征参数的分类与组成，对比阐述测试方法中各关键问题的发展现状及趋势，总结需要深入研究的内容，为低约束试件断裂韧性测试发展提供一定依据。

1 低约束试件断裂韧性测试发展

SENT 试件根据其加载方式和几何特征可分为夹持型和销钉型，通常销钉式SENT 试件用于测试管道轴向裂纹，而夹持型SENT 试件用于测试管道的环向裂纹。由于环向裂纹是基于应变设计的主要研究问题，因而夹持型SENT 试件已成为低约束断裂测试方法的研究热点。

关于低约束试件断裂韧性测试最早可追溯到1962 年，Irwin、Krafft 和Sullivan 为了测量弹性平面应变断裂韧度在美国材料与试验协会会议上首次提出了SENT 试样的概念。1964 年, Sullivan[12]提出了一种销钉式SENT 试件，Srawley 等[13]采用该试件测试了弹性能量释放率(G)。1965 年，Srawley等[14]提出了销钉式SENT 试样应力强度因子(K)的封闭解。1973 年，Tada 等[15]获得了销钉式SENT试件较为准确的应力强度因子方程和的柔度方程。

2006 年，挪威船级社为评估海底浅裂纹管道的断裂韧性，出版了管道低约束SENT 试件断裂韧性测试标准DNV-RP-F108[16]。该标准采用夹持型或销钉型SENT 试样测试材料的J 积分阻力曲线(J–R)。DNV 建议试件进行疲劳裂纹预制，预裂纹长度0.2 ≥a/W≥0.5，试件不需要开侧槽，最大裂纹扩展长度为3 mm。DNV 采用多试样法，要求至少测试6 个有效SENT 试件。该方法不考虑裂纹扩展修正，因而裂纹扩展较短时，该方法简单实用。考虑焊缝强度匹配和延性裂纹扩展等因素造成的不确定性，该方法在J 积分塑性因子的表达式中添加了安全系数0.85，该安全系数可能导致断裂韧性偏于保守，且测试所需时间与材料成本较大。

2008 年，加拿大矿物与能源研究中心 Shen等[7-8]参考ASTM E1820 中SENB 试样J–R 曲线试验流程，提出了一种单试件方法，用于评估夹持型SENT 试件的J–R 阻力曲线。该方法要求试样的宽度和厚度相等(W=B)，两个夹持端之间的距离H=10W，预制疲劳裂纹的长度0.1 ≥a0/W≥0.7。为了保证裂纹前缘平直扩展以及裂纹尖端附近处于平面应变条件，该方法建议开侧槽，侧槽占试件厚度的7.5%。采用单应变规测量裂纹嘴张开位移(crack mouth opening displacement, CMOD)，使用卸载柔度法估算裂纹扩展长度。

2009 年，巴西圣保罗大学Gravero 等[17-18]、Mathias 等[19]和Ruggieri[20]提出了使用卸载柔度法测试单个SENT 试件J–R 曲线的方法。该方法与加拿大矿物与能源研究中心提出的测试方法以及ASTM E1820 标准方法类似，但各方法中应力强度因子、J积分塑性因子以及基于 CMOD 的柔度方程不尽相同。

2010 年，埃克森美孚公司提出了一种使用双应变规测量单个试件CTOD 阻力曲线(CTOD–R)的方法[9]。该方法建议对试件进行疲劳裂纹预制或使用直径不大于0.15 mm 的线切割(electrical discharge machining, EDM) 加工，以确保初始长度在0.25 ≥a0/W≥0.35 的范围内。EDM 可使切口前沿均匀，初始裂纹长度更精确，对于高韧性管线钢和焊缝建议采用，但对于低断裂韧性材料，EDM 方法可能会导致断裂韧性偏高。该方法建议试件侧槽深度占试件厚度的5%。

2013 年，比利时根特大学的Verstraete 等[21-23]提出了一种采用单个试件测试材料CTOD–R 曲线的方法。虽然其CTOD 测试也采用DCG 方法，但CTOD 的定义与埃克森美孚方法的定义不同。裂纹扩展长度测量上采用直流电位梯度法(direct current potential drop，DCPD)。

2014 年，英国标准协会基于上述测试方法，制定了SENT 试件断裂韧性测试标准BS 8571[10]。该标准包括J–R 曲线和CTOD–R 曲线测试流程，而J–R 曲线试验又分为多试样法和单试样法。J 积分方程与标准DNV-RP-F108 所用方程式相同，不考虑裂纹扩展修正。采用双应变规方法确定CTOD，CTOD计算与埃克森美孚方法[9]不同。BS 8571 中允许使用销钉型和夹持型SENT 试件，但仅对夹持型SENT试件的测试流程进行了详尽阐述。各低约束试件断裂韧性测试方法的具体参数对比见表1，不同方法中试件的几何尺寸、侧槽深度、初始裂纹长度、断裂韧性表征参数等不尽相同。

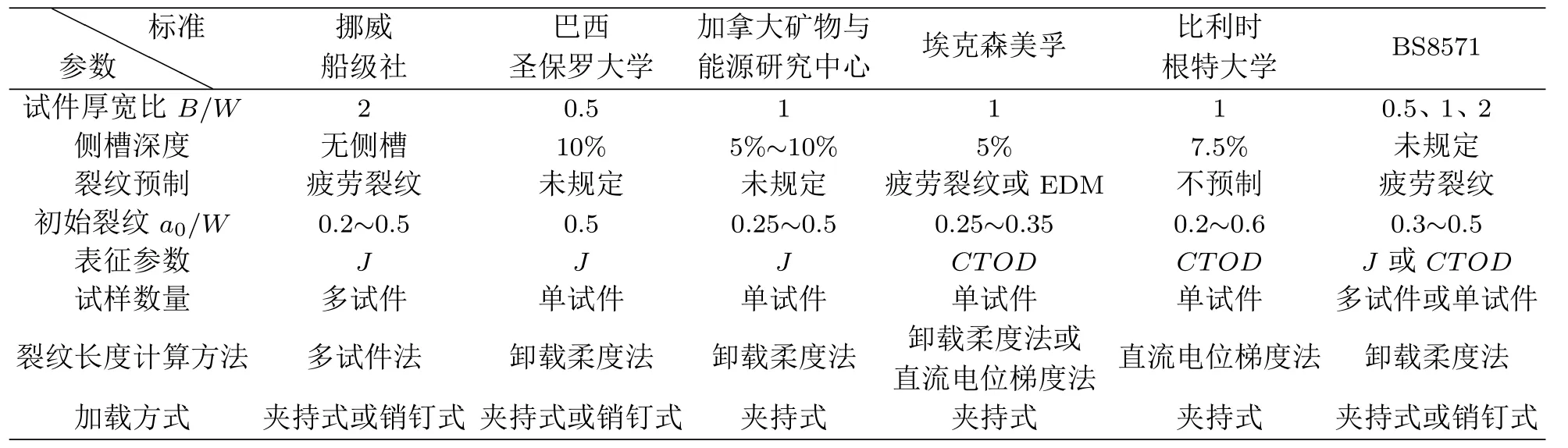
表1 SENT 试件断裂韧性测试方法对比

2 断裂韧性表征参数

2.1 CTOD

断裂韧性测试过程中，通常采用CTOD 或者J积分进行材料性能表征。1963 年，Wells[24]在英国焊接研究所中首次提出CTOD 的概念，Wells 将其称为裂纹张开位移(COD)，但为区别于CMOD，将其名称改为CTOD。CTOD 常见的定义方式有三种，即原始裂纹尖端位移、裂纹尖端90◦角截距位移和原始裂纹尖端90◦角截距位移(见图1)。

由于局部塑性变形，加载后裂纹尖端钝化。如果加载时，远离裂纹尖端的裂纹表面未变形，只围绕韧带上一点进行刚性旋转，且与初始裂尖处的钝裂纹前缘相切，则两切点之间的距离即为原始裂纹尖端位移。原始裂纹尖端位移已用于BS 8571[10]和埃克森美孚双应变规方法的CTOD 测试中，该CTOD定义与裂纹尺寸和材料硬化响应有关，如果切点位于原始裂纹尖端后，则会高估实际CTOD 值。

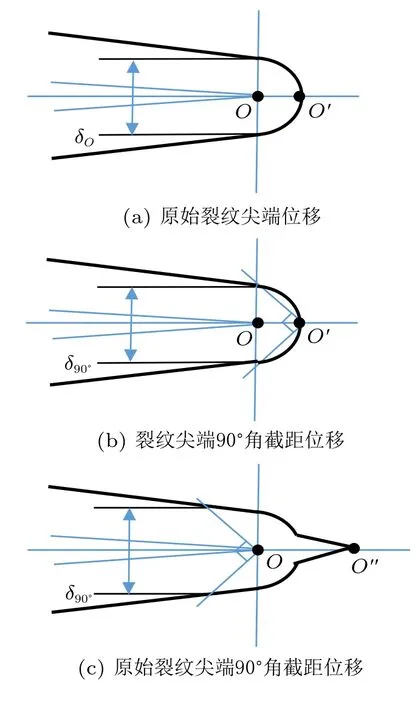
图1 CTOD 的分类

为了便于在有限元分析中计算裂纹的CTOD，将钝化裂纹尖端开始的两条垂直直线与裂纹表面的截距作为裂纹尖端90◦角截距位移。由于在试件有限元模拟中的便利性，该CTOD 定义得到广泛应用，但不适用于扩展裂纹。加拿大矿物与能源研究中心研究J 积分与CTOD 转换关系时，采用了此定义计算CTOD。

韧性材料裂纹尖端在加载后会发生钝化现象，但随着加载过程钝化裂纹会再次形成尖裂纹，因此裂纹扩展时裂纹尖端90◦角截距位移便失去其物理意义。Verstraete 等[23]和Van 等[25]基于裂纹扩展的刚性旋转假设，提出了原始裂纹尖端90◦角截距位移的定义，该方法使裂纹扩展时的CTOD 具有可比性。

2.2 J 积分

Rice[26]于1967 年提出J 积分作为表征弹塑性材料裂纹尖端应力应变场的参数。在断裂韧性试验中，可将J 积分分为弹性J 积分和塑性J 积分分别进行计算，如式(1) 所示

式中，Jel和Jpl分别表示J 积分的弹性分量和塑性分量。

Jel与应力强度因子有关，按式(2) 计算

式中，ν是泊松比，E是杨氏模量。KI为I 型裂纹应力强度因子，由载荷和裂纹尺寸通过式(3) 确定

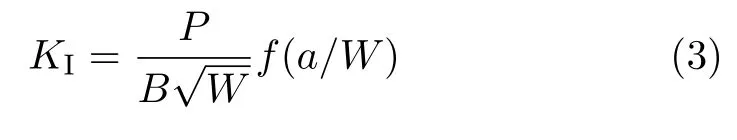
式中，a为裂纹长度，W为试样宽度，B为试样厚度，P为载荷，f(a/W) 为几何因子。

J积分的塑性分量可通过引入塑性因子(η) 与载荷位移曲线下塑性区面积，由式(4) 计算

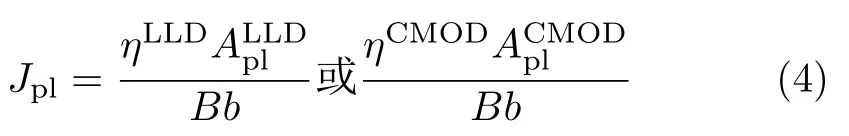
式中，b是韧带的长度，分别代表载荷与载荷线位移(load line displacement，LLD) 或CMOD 曲线下塑性区的面积(见图2)。

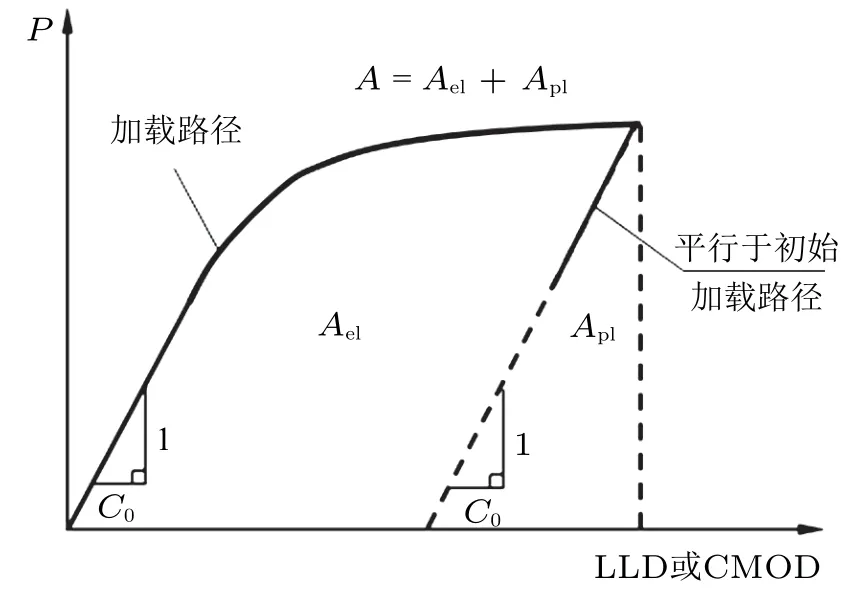
图2 载荷−位移曲线下塑性区示意图

3 低约束试件断裂韧性测试关键问题

3.1 应力强度因子

J 积分的弹性部分与应力强度因子有关，应力强度因子的准确性对总J 积分的计算有直接影响。对于夹持型SENT 试件，挪威船级社采用了Ahmad等[27]提出的应力强度因子解析解。加拿大矿物与能源研究中心通过在弹性和平面应变条件下的有限元计算分析，提出了夹持型SENT 试件应力强度因子的数值解。部分学者先后使用有限元分析法或回归分析法得到应力强度因子不同的计算式，结果对比见图3，可知各应力强度因子计算方法在其适用范围内基本一致[28-29]。以Zhu[30]提出的应力强度因子全范围解析解为参考，各方法中几何因子的最大相对误差不超过3% (见图4)，而Zhu[30]方法的适用范围更广，精确度较高，建议使用其计算夹持型SENT 试件的应力强度因子。

图3 应力强度因子对比

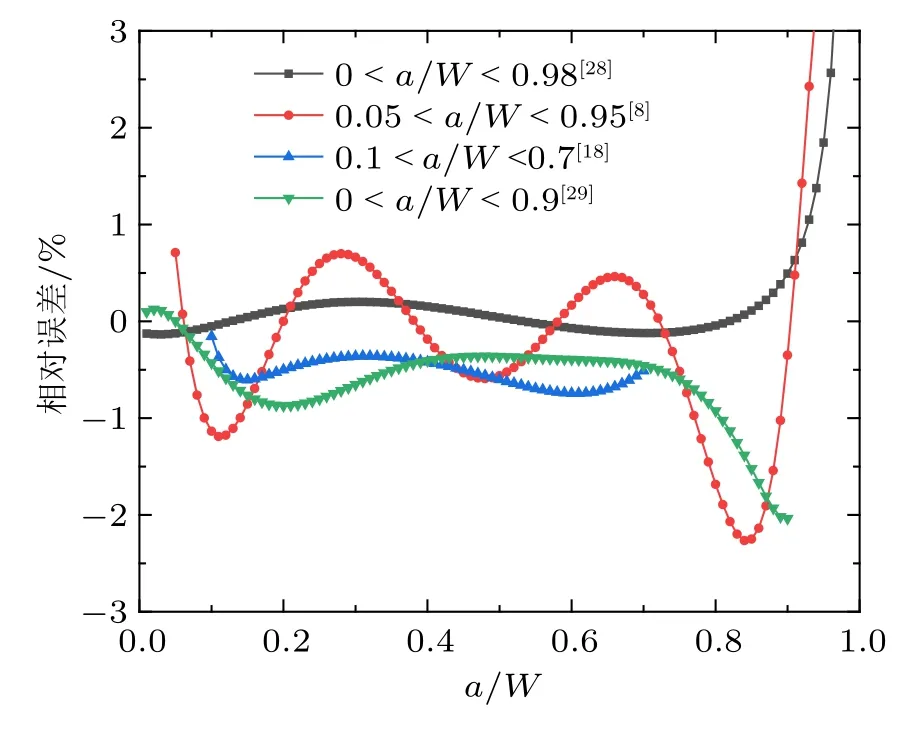
图4 几何因子相对误差

3.2 J 积分塑性因子

挪威船级社[16]、加拿大矿物与能源研究中心[7-8]和巴西圣保罗大学[18-19]等先后提出了夹持型SENT试件J 积分塑性因子的不同表达式。2006 年，挪威船级社根据三维有限元分析的数值结果，提出了与裂纹深度和试件厚度有关的五阶多项式作为塑性因子评估方程。Shen 等[8]基于Ramberg–Osgood 硬化模型，采用平面应变有限元分析，拟合得到塑性因子多项式函数。巴西圣保罗大学的Cravero 等[18]提出塑性因子与应变硬化性能无关理论，并以简单的线性函数表示J 积分塑性因子。Mathias 等[19]根据巴西圣保罗大学的数值结果[18,20]，通过拟合得到J 积分塑性因子的五阶多项式函数。标准BS 8571 中J积分塑性因子的计算与试件的厚宽比有关，当试件厚宽比1 ≥B/W≥2 时，采用挪威船级社使用的塑性因子方程；当试件厚宽比1/2 ≥B/W≥1 时，采用加拿大矿物与能源研究中心使用的塑性因子方程。Huang 等[31]和Wang 等[32]对有侧槽和无侧槽夹持型SENT 试样进行有限元分析，并提出了与试件裂纹深度、厚宽比以及应变硬化指数有关的J 积分塑性因子方程。

各方法中J 积分塑性因子结果对比见图5。对于基于载荷线位移的J 积分塑性因子，除Huang 方法外，其余三种方法的结果较为接近，而Huang 提出的塑性因子是在考虑试件侧槽的基础上进行的，因而结果偏高；加拿大矿物与能源研究中心提出的塑性因子适用范围更广，建议使用。对于基于裂纹嘴张开位移的J 积分塑性因子，挪威船级社方法明显高于其他方法。巴西圣保罗大学方法中塑性因子与裂纹深度成线性关系，精度较低，不建议采用；加拿大矿物与能源研究中心方法在0.05 ≥a/W≥0.65 范围内建议使用，其余方法在各自的适用范围内偏差较小，而更为精确的J 积分塑性因子的表达式有待深入研究。

图5 J 积分塑性因子结果对比

3.3 J 积分与CTOD 转换因子

SENT 试件的CTOD 阻力曲线测试通常可采用J 积分转换法或双应变规法。Zhu 等[33]采用这两种方法分别对高、低应变硬化性能钢进行测试，发现采用不同J 积分转换因子得到的CTOD 阻力曲线不同，而双应变规法测定的CTOD 阻力曲线相近。特别是对于高应变硬化钢，两种方法的CTOD–R 曲线明显不同。因而J 积分转换因子的准确性对CTOD阻力曲线有直接影响。对于夹持型SENT 试件，J积分转换法公式参考标准ASTM E1820，采用式(5)计算

式中，m为J 积分与CTOD 转换因子，σY为屈服强度。

部分学者先后提出 SENT 试件的 J 积分与CTOD 转换因子表达式，通过对比发现：CANMET方法中转换因子是基于有限元分析的线性拟合，故应用范围受限；Huang 等[34]提出的转换因子会导致低应变硬化材料的CTOD 阻力曲线偏高。各转换因子方程在硬化指数n=10，单边侧槽深度为7.5%时的对比结果见图6。可知，Moreira 等[35]和Ruggieri[36]方法中两个平面应变转换因子具有可比性，差异较小，均低于Sarzosa 等[37]方法的转换因子，但在没有额外有限元分析结果的条件下，很难确定现有结果的精确性。因此，需要进一步的研究，以确定一个更准确的J 积分与CTOD 转换因子。

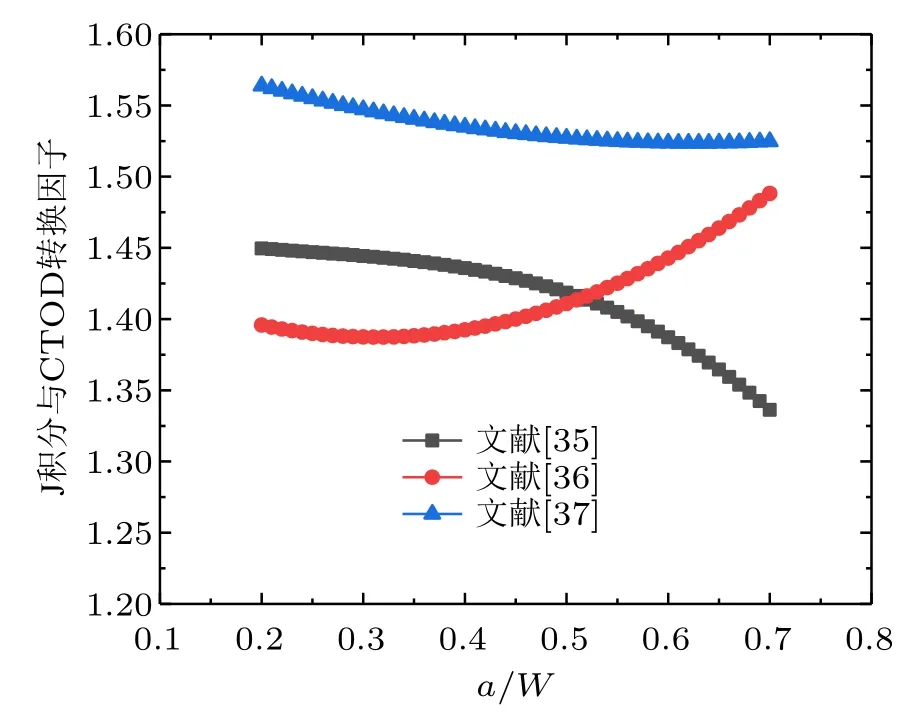
图6 J 积分与CTOD 转换因子结果对比

3.4 裂纹尺寸的测量

3.4.1 卸载柔度法

使用单试样法进行断裂韧性测试时，除了测试断裂表征参数，还需测试裂纹扩展长度，常用裂纹长度的测量方法分为卸载柔度法和直流电位梯度法。卸载柔度法是一种通过监测载荷和裂纹嘴张开位移计算裂纹长度的方法。卸载柔度法在SENB 和CT 试件断裂韧性测试中已有广泛应用，而对于低约束SENT试件，Verstraete 等[38]通过数值模拟和实验分析证实了卸载柔度法的有效性。不同的测试方法所规定的柔度方程不尽相同，而如何确定一个相对准确的柔度方程成为了研究的交点。加拿大矿物与能源研究中心、埃克森美孚公司、巴西圣保罗大学、Tyson等均提出了各自柔度方程。

将上述四个柔度方程与三组独立的有限元计算结果进行比较，发现三组有限元分析结果基本一致，且与加拿大矿物与能源研究中心和巴西圣保罗大学提出的结果接近，而埃克森美孚公司和Tyson 的结果与有限元分析存在明显偏差。因此，目前应使用加拿大矿物与能源研究中心或巴西圣保罗大学提出的柔度方程。使用卸载柔度法计算裂纹尺寸时，会在初始位置出现裂纹负增长的情况，所以还需参考标准ASTM E1820 对初始裂纹尺寸进行修正。

3.4.2 直流电位梯度法

直流电位技术已广泛应用于试件、管道和压力容器的裂纹尺寸监测[39-40]，该方法假定远离裂纹平面的电流分布均匀，且穿过裂纹的电位降与裂纹长度呈单调递增关系，电场的唯一扰动是由裂纹的存在引起的。

1965 年，Johnson 将受拉伸载荷中心裂纹板的输入电压与裂纹长度联系起来，提出了一个解析校准方程。比利时根特大学[21-23]又通过实验证实该方程可用于校准SENT 试样的电位降与裂纹长度之间的关系。Geldhof 和Vertraete 通过对实验结果的比较，证明直流电位技术和卸载柔度法在用于确定SENT 试件裂纹扩展阻力曲线的精度是等效的。但从实验操作角度，直流电位梯度法需要设备较多，实验流程偏于复杂，建议采用卸载柔度法进行实验。

3.5 J 积分直接测量技术

2015 年，Weeks 等[41]采用Prandtl–Reuss 增量理论，提出了一种使用表面应变计直接测量夹持型SENT 试件J 积分的实验方法，结果表明，在裂纹扩展1 mm 范围内直接测量得到的J–R 曲线与CANMET 法测定的曲线基本一致。2016 年，Weeks等[42]对实验技术进行改进，测试了X65 管道钢母材与焊缝的J–R 曲线，通过使用数字图像相关技术测量试件的表面应变和远端位移，进而直接计算J 积分，结果发现整个实验过程中数字图像相关技术直接测量的J 积分与CANMET 方法测试的结果相同。数字图像相关技术可以测试试件表面的整体应变情况，比在表面安装应变计更加可靠，且该方法即不需要使用基于CMOD 的J 积分方程，也不需要测量裂纹尺寸的其他装置，因而J 积分直接测量技术对于验证基于CMOD 的增量J 积分方程以及J–R 阻力曲线具有重要的意义。